2002年陕西省高三教学质量检测试题(一)
数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至3页,第Ⅱ卷3至8页。满分150分,考试时间120分钟。
| 题号 | 一 | 二 | 三 | 总分 | |||||
| (17) | (18) | (19) | (20) | (21) | (22) | ||||
| 得分 | |||||||||
参考公式:
(1)三角函数的和差化积公式
![]()
![]()
![]()
![]()
(2)正棱台、圆台的侧面积公式
![]()
其中c′、c分别表示上、下底面周长,l表示斜面高或母线长。
(3)台体的体积公式
![]()
其中S′、S分别表示上、下底面积,h是高。
第Ⅰ卷(选择题,共60分)
1.在第Ⅰ卷的密封线内填写地(市)、县(市)、学校、班级、姓名、学号(或考号)。
2.将第Ⅰ卷的答案填写在下面表格内。
| 题号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
| 答案 |
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)如图1,I是全集,![]() ,
,![]() ,则阴影部分所表示的集合是( )
,则阴影部分所表示的集合是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
(2)过点P(1,2)的直线交圆![]() 于两点A、B,若点P是弦AB的中点,则弦AB所在直线的方程是( )
于两点A、B,若点P是弦AB的中点,则弦AB所在直线的方程是( )
A.2x+y+3=0 B.2x-y-3=0 C.x+2y-4=0 D.x-2y+3=0
(3)空间四条直线a、b、c、d,其中a⊥c,b⊥c,a⊥d,b⊥d,那么a与b,c与d这两对( )
A.都平行 B.都不平行 C.至少有一对平行 D.至多有一对平行
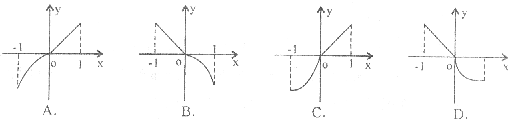
(4)设函数![]() ,则其反函数的图象为( )
,则其反函数的图象为( )
(5)等差数列![]() 中,
中,![]() ,
,![]() ,
,![]() ,则n为( )
,则n为( )
A.8 B.9 C.10 D.11
(6)(理)在极坐标系中,曲线![]() 与直线
与直线![]() 之间的位置关系为(
)
之间的位置关系为(
)
A.相离 B.相切 C.相交 D.以上都有可能
(文)已知∈(0,2π),使sinα+cosα<0的角α的取值范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(7)有如下四个命题:
①若函数![]() 的周期为2π,则k=1;
的周期为2π,则k=1;
②函数![]() 是偶函数;
是偶函数;
③函数![]() 在
在![]() 上是增函数;
上是增函数;
④函数![]() 的最大值是2。
的最大值是2。
其中,正确命题是( )
A.①③ B.①④ C.②③ D.②④
(8)抛物线![]() 上一点M到焦点的距离是3,那么M到y轴的距离是( )
上一点M到焦点的距离是3,那么M到y轴的距离是( )
A.3 B.4 C.5 D.6
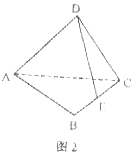
(9)如图2,将正方形ABCD沿对角线AC折成直二面角,E是BC的中点,异面直线AB与DE所成角的正切值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(10)若![]() 存在,则实数x的取值范围是( )
存在,则实数x的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(11)有一圆形铁皮,欲制作等长母线的两个无底圆锥形容器,要求两个容器的侧面正好用完铁皮,且侧面面积之比为1:2,则这两个容器的高之比为( )
A.2:1 B.8:5
C.![]() D.
D.![]()
(12)某校准备召开高中毕业生代表会,把6个代表名额分配给高三年级的3个班,每班至少一个名额,不同的分配方案共有( )
A.7 B.9 C.10 D.12
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分。
(13)离心率为![]() ,一条准线为x=-4的椭圆的标准方程是____________。
,一条准线为x=-4的椭圆的标准方程是____________。
(14)如果n为偶数,且![]() ,则
,则![]() 的展开式中的常数项为____________。
的展开式中的常数项为____________。
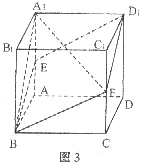
(15)如图3,已知正方体![]() 是棱长为a的正方体,E、F分别是棱
是棱长为a的正方体,E、F分别是棱![]() 和
和![]() 的中点,则四棱锥
的中点,则四棱锥![]() 的体积为_____________。
的体积为_____________。
(16)已知![]() ,
,![]() ,则方程f[g(x)]+3g[f(x)]=-2的解为___________。
,则方程f[g(x)]+3g[f(x)]=-2的解为___________。
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程式演算步骤。
(17)(本小题满分12分)
设![]() 、
、![]() 是两个非零复数,且满足
是两个非零复数,且满足![]() ,
,![]()
(Ⅰ)求![]() 的辐角主值;
的辐角主值;
(Ⅱ)如果![]() 、
、![]() 对应的点分别为A、B,求
对应的点分别为A、B,求![]() 的面积。
的面积。
(18)(本小题满分12分)
已知n是大于1的自数,函数![]() ,
,
(Ⅰ)试判断函数f(n)的增减性;
(Ⅱ)若不等式![]() 恒成立,求满足条件的最大的正整数m。
恒成立,求满足条件的最大的正整数m。
(19)(本小题满分12分)
已知如图4,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,又PC⊥平面ABCD,PC=a,E为PA的中点。
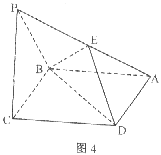
(Ⅰ)求证:平面EBD⊥平面ABCD;
(Ⅱ)求点E到平面PBC的距离;
(Ⅲ)求二面角A-BE-D的正切值。
(20)(本小题满分12分)
我省某县位于沙漠边缘地带,为了早日实现沙漠变绿洲,到1998年年底全县的绿化率已达30%。从1999年开始,每年将出现这样的局面,原有沙漠面积的16%被栽上树改造为绿洲,同时,原有绿洲面积的4%又被侵蚀,变为沙漠。
(Ⅰ)设全县面积为单位1,1998年年底绿洲面积为![]() ,经过一年绿洲面积为
,经过一年绿洲面积为![]() ,经过n年绿洲面积为
,经过n年绿洲面积为![]() ,求证
,求证![]() ;
;
(Ⅱ)今年(2002)年底全县的绿洲面积能否超过60%。
(21)(本小题满分12分)
已知函数![]() 、
、![]() ,设F(x)=f(x)+g(x),如果f(x)、g(x)的图象都经过(1,1)点,且
,设F(x)=f(x)+g(x),如果f(x)、g(x)的图象都经过(1,1)点,且![]() 。
。
(Ⅰ)求F(x)的解析式;
(Ⅱ)设正项数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,计算
,计算![]() 、
、![]() 、
、![]() 的值,由此猜想
的值,由此猜想![]() 的表达式,并用数学归纳法证明。
的表达式,并用数学归纳法证明。
(22)(本小题满分14分)
已知如图5,椭圆![]() 的方程为
的方程为![]() ,其两焦点为
,其两焦点为![]() 、
、![]() ,双曲线
,双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,且以
,且以![]() 、
、![]() 为焦点。
为焦点。
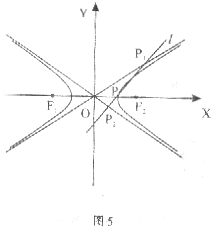
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设P为![]() 上一点,过P的直线l交
上一点,过P的直线l交![]() 的渐近线于
的渐近线于![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的面积。
的面积。
参考答案:
一、选择题
| 题号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | |
| 答案 | B | D | C | C | C | 理 | 文 | D | A | B | B | C | C |
| A | C | ||||||||||||
二、填空题
(13)![]() (14)20 (15)
(14)20 (15)![]() (16)1
(16)1
三、解答题(解答题只给出一种解法的评分标准,各题的其它正确解法可参照相应试题所给解法的评分标准赋分)
(17)解:(Ⅰ)∵![]() ,
,
∴![]() 。………………………………………………(2分)
。………………………………………………(2分)
∴![]() 。…………………………………(4分)
。…………………………………(4分)
故![]() 或
或![]() 。……………………………………………(6分)
。……………………………………………(6分)
(Ⅱ)由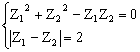 ,可得
,可得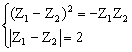 …………(8分)
…………(8分)
∴![]()
∴![]() 。……………………………………(9分)
。……………………………………(9分)
由(Ⅰ)知![]() …………………………(10分)
…………………………(10分)
∴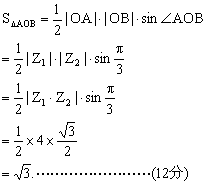
(18)解:(Ⅰ)∵![]() ,(n>1的自然数)
,(n>1的自然数)
∴![]()
![]() ………………(2分)
………………(2分)
∴![]()
![]() …………………………(4分)
…………………………(4分)
∴f(n)是关于自然数n(n>1)的增函数。………………(5分)
(Ⅱ)要使![]() ,对大于1的自然数n恒成立。
,对大于1的自然数n恒成立。
即![]() 恒成立。…………………………(7分)
恒成立。…………………………(7分)
只须f(n)的最小值大于![]() 即可 ∴
即可 ∴![]() ……………………(9分)
……………………(9分)
即 ![]() ∴m<14。…………………………(11分)
∴m<14。…………………………(11分)
故满足条件的最大正整数m=13……………………………(12分)
19.(Ⅰ)证明:连结AC交BD于点O,连结OE,则O是AC的中点。又知E是AP中点
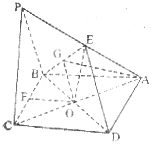
∴![]() ………………………………(2分)
………………………………(2分)
∵PC⊥平面ABCD,∴OE⊥平面ABCD。又知 ![]() 平面BDE,
平面BDE,
∴平面EBD⊥平面ABCD。………………(4分)
(Ⅱ)由(Ⅰ)可知OE//PC,则OE//平面PBC。
∴点E到平面PBC的距离等于点O到平面PBC的距离
∴过O作OF⊥BC交BC于F,
∴OF即为所求………………………………(6分)
∵四边形ABCD是菱形,边长为a,∠ABC=120°
∴∠CBD=60°DB=BC=a,∴![]() ,
,
∴![]() 。…………………………(8分)
。…………………………(8分)
故点E到平面PBC的距离为![]() 。
。
(Ⅲ)由(Ⅰ)可知,OE⊥OA,OA⊥BD
∴OA⊥平面BDE。
过O作OG⊥BE,垂足为G,连结AG,则∠AGO为二面角A-BE-D的
平面角…………10(分)
∵PC=a ∴![]() ,
,![]()
∴Rt△BOE为等腰直角三角形
∴![]() ,
,
又知 ![]() ∴Rt△AOG中,
∴Rt△AOG中,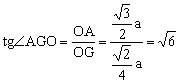 。
。
∴所求二面角A-BE-D的正切值为![]() 。……………………(12分)
。……………………(12分)
(20)(Ⅰ)证明:∵第n年年底绿洲面积为![]() ,
,
∴第n年年底的沙漠面积为![]() …………………………(1分)
…………………………(1分)
根据题意,经过n年(即第n+1年)的绿洲面积
![]() ……………………………(3分)
……………………………(3分)
![]()
即 ![]() …………………………………………(5分)
…………………………………………(5分)
(Ⅱ)由(Ⅰ)知![]() 从98年到2002年底,经过4年改造,绿洲面积
从98年到2002年底,经过4年改造,绿洲面积![]() …………………………………………………(7分)
…………………………………………………(7分)
∴![]()
![]() …………………………(9分)
…………………………(9分)
即![]()
![]() …………………………(11分)
…………………………(11分)
∴2002年年底全县的绿洲面积还不能超过60%……………………(12分)
(21)解:(Ⅰ)∵![]() ,
,![]() 的图象都经过(1,1)点,∴a=1,b=1
的图象都经过(1,1)点,∴a=1,b=1
∴![]() ,
,![]() …………………………(2分)
…………………………(2分)
又 ![]() ,∴
,∴![]() 。
。
即 ![]() ∴
∴![]() 或
或![]()
从而n=1,n=-1(舍去)
故![]() …………………………(4分)
…………………………(4分)
(Ⅱ)由![]() 得
得![]()
当n=1时,![]() ,∴
,∴![]() …………………………(5分)
…………………………(5分)
当n=2时,![]()
∴![]() ∴
∴![]() ………………………………(6分)
………………………………(6分)
当n=3时,![]()
∴![]() ∴
∴![]() …………………………(7分)
…………………………(7分)
据此推测 ![]() ………………………………………(9分)
………………………………………(9分)
以下用数学归纳法证明:
①当n=1时,结论显然成立。
②假设当n=k时,结论成立。即![]()
∴![]() …………(*)……………………(10分)
…………(*)……………………(10分)
则当n=k+1时,![]()
∴![]() 代入(*)得
代入(*)得
![]()
∴![]() 即 当n=k+1时结论也成立
即 当n=k+1时结论也成立
综上可知,对n∈N的一切自然数结论成立 …………………………(12分)
(22)解:(Ⅰ)由![]() 知,
知,![]() ,
,![]() ,………………(2分)
,………………(2分)
∴![]()
∵![]() 的渐近线为
的渐近线为![]() ,
,
故可设其方程为![]() (λ>0)…………………………(4分)
(λ>0)…………………………(4分)
又∵椭圆与双曲线共焦点 ∴
![]()
故![]() 的方程为
的方程为![]() 即
即![]() ……………………(6分)
……………………(6分)
(Ⅱ)设l与![]() 交于
交于![]() ,与
,与![]() 交于
交于![]()
∵![]() ,由定比分点坐标公式,得
,由定比分点坐标公式,得
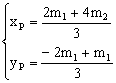
由P在双曲线上知,![]() ………………(8分)
………………(8分)
∴![]() 即
即![]() …………………(10分)
…………………(10分)
又![]() ,
,![]() ,而
,而
![]() ……………………(12分)
……………………(12分)
∴![]()
![]() …………………………(14分)
…………………………(14分)