几何综合练习(四)

综合练习 (四)

班级：______________，姓名：___________________, 成绩：________________

一. 选择题：(每小题5分，共5×12 = 60分)将正确答案填入下表中

1. 设集合A = {1, 5}，则满足AB = {1, 5}的集合B的个数是
　　　(A) 4　　(B) 3　　(C) 2　　(D) 1

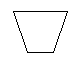
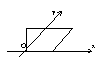
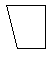
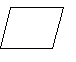
2. 如图为一平面图形的直观图，则此平面图形可能是

　　　  (A)　　　　　　 (B)　　　　　  (C)　　　　　  (D)

3. 若关于x的一元二次方程x² + px + q = 0 (p ¹ 0)恰有两个纯虚数根，则
　　　(A) p, q Î R且q > 0　(B) p Î R, q为纯虚数　(C) p为纯虚数, q Î R  (D) p, q都是纯虚数

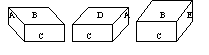
4. 长方体的6个面分别标有A, B, C, D, E, F这六个字母中的一个，现放成下面三个不同的位置，则字母A, B, C对面的字母分别是

　　  (A) D, E, F　(B) F, D, E　(C) E, F, D　(D) E, D, F

5. 正三棱台侧面与底面所成的角为45°，那么它的侧棱与底面所成角的大小是
　　　(A) arctg2　 (B) arctg　 (C) arcctg2　 (D) arcctg　

6. DABC的三边a, b, c满足+=，则角B等于
　　　(A) 30°　　(B) 45°　　(C) 60°　　(D) 120°

7. 若f (x)为奇函数，且在(0,+¥)内是增函数，又f (－3) = 0，则xf(x) < 0的解集为
　　　(A) (－3,0)(0,3)　 (B) (－¥,－3)(0,3)　 (C) (－¥,－3)(3,+¥)　 (D) (－3,0)(3,+¥)　

8. 设A = 3⁷ + C3⁵ + C3³ + C3,　B = C3⁶ + C3⁴ + C3²，则A－B的值是

　　  (A) 128　 (B) 129　 (C) 4⁷　 (D) 0　

9. 设双曲线－= 1(a>0, b>0)的离心率eÎ[, 2]. 令双曲线的两条渐近线构成的角中以实轴为角平分线的角为q，则q的取值范围是　
　　　(A) [,]　　(B) [,]　　(C) [,]　　 (D) [, p]

10. 已知a = (lgx²)(lgy²), b = lg²(xy), c = [lg(x² + y²)]²，其中x > 0, y > 0, x² + y² < 1, x ¹ y, 则a, b, c的

　　大小顺序是
　　　(A) c < b < a　 (B) c < a < b　　(C) a < b < c　 (D) a < c < b　

11. 银行发行奖券号码由000001－999999，规定第1, 3, 5位(从个位算起)是互不相等的奇数，第2, 4,

　　6位全是偶数(数字可以重复)的可以中奖，则中奖的奖券共有
　　　(A) 100张　 (B) 600张　 (C) 3600张　 (D) 7500张　

12. 已知函数f (x)对x > 0有意义，且f (2) = 1, f (m·n) = f (m) + f (n)，则
　　　(A) f () < f (4) (B) f () = f (4) (C) f () > f (4) (D) f ()与f (4)的大小关系不确定

二. 填空题：(每小题4分，共4×4 = 16分)

13. 用一个与圆柱母线成60°角的平面截圆柱，则截口椭圆的离心率是_______________ .

14. 公路上依次有四点A, B, C, D. 一步行者以5km/h的速度从A出发向点D行进，到达点D后立刻返回到点B，一共化了5小时. 已知他走完A到C之间的距离要用3小时，并且A与B, B与C, C与D之间的距离(按所给的次序)构成等比数列，则点B与C之间的距离为___________km.

15. 圆锥的母线长为2cm，侧面积为2pcm²，圆锥的顶点和底面圆周在同一个球面上，则此球的

　 体积是________cm³ .

16. 给出下列命题：①存在实数a，使sinacosa = 1；②存在实数a，使sina + cosa =; ③函数y =

　　sin (－2x)是偶函数；④若a,b是第一象限角，且a > b，则tga > tgb；⑤在DABC中，A > B

　　是sinA > sinB的充要条件. 其中正确命题的序号是________________________ .

三. 解答题：(第17～21题每题12分，第22题14分，共74分)

17. 已知复数z₁, z₂对应于复平面上圆心在原点，半径为的圆周上的两点，且+= 4－3i，求复数z₁z₂,

18. 设各项均为正数的数列{a_n}的前n项和为S_n，且存在正数t，使对所有的自然数n都有=成立. (1)求数列{a_n}的通项公式；(2)如果< t，求t的取值范围.

19. 已知直三棱柱ABC－A₁B₁C₁中，AB = AC, D为BC中点，F为BB₁上一点，且BF = BC = 2, FB₁ = 1. (1)若E为AD上不同于A, D的任一点，求证：EF^FC₁；(2)若A₁B₁ = 3, 求FC₁与平面AA₁B₁B所成角的大小；(3)在(2)的条件下，求点C₁在A₁B_1­上的射影到平面A₁FC₁的距离.

20. 某工厂今年一月、二月、三月生产某种产品的产量分别为1万件、1.2万件、1.3万件，为了估测以后每月的产量，以这三个月的产量为依据，用一个函数模拟该产品的月产量与月份数x的关系，模拟函数可以用二次函数或函数y = a×b^x + c (其中a, b, c为常数). 已知四月份该产品的产量为1.373万件，问用以上哪个函数作为模拟函数较好？请说明理由. 并根据所得结论预测五月份的产量.

21. 一条抛物线的准线方程为y =，焦点在射线y =x (x > 0)上，且经过坐标原点. (1).求抛物线方程；(2).设抛物线与x轴另一个交点为B，P、Q为抛物线上的两个不同的动点，当点P在抛物线上运动时，如果使BP^PQ，求点Q的存在范围.

22. 已知函数f (x) = 6x－6x²，记函数g₁ (x) = f (x), g₂ (x) = f [g₁(x)], g₃ (x) = f [g₂ (x)], …, g_n (x) = f [g_n-1 (x)], …. (1)求证：如果 存在一个实数x₀，满足g₁ (x₀) = x₀，那么对一切n Î N, g_n (x₀) = x₀都成立；(2)若实数x₀满足g_n (x₀) = x₀，则称x₀为不动点，试求出所有这些不动点；(3)考察区间A = (－¥, 0)，对于任意x Î A，有g₁ (x) = f (x) = a < 0, g₂ (x) = f [g₁ (x)] = f (a) < 0，且n > 2时，g_n (x) < 0. 试问是否存在区间B (BA = Æ)，对于区间B内的任意实数x都有g_n (x) < 0 (n > 2).

参考答案：

一．

1	2	3	4	5	6	7	8	9	10	11	12
A	D	C	D	C	C	A	B	A	B	D	B

二. 13. 1/2;14. 5; 15.32p/3cm³;16.②③⑤;

三.17.设z₁ = 1/5 (cosa + isina), z₂ = 1/5 (cosb + isinb)由条件得sina + sinb = 3/5且cosa + cosb = 4/5，从而tg(a+b)/2 = 3/4, cos(a+b)=7/25, sin(a+b)=24/25∴z₁z₂ =1/25 [cos(a+b)+isin(a+b)] = 7/625 + 24/625 i.

18.(1)a_n=(2n-1)t; (2)t>1/³Ö4 ;

19. (2)arcsin4Ö10/15; (3)28Ö82/369;

20.设二次函数为f (x) = mx² + px + q，由f (1) = 1, f(2) = 1.2, f (3) = 1.3，得f (x) = -0.05x² + 0.35x + 0.7，类似可得g(x) = a×b^x + c = 0.8×0.5^x + 1.4. 而f (4) - 1.37 = 0.07, g(4) - 1.37 = 0.02∴使用函数y = 0.8×0.5^x + 1.4作为模拟函数较好；g (5) = 1.375 (万件)

21. (1). y = -x² + 2x; (2). 点Q的存在范围是抛物线y = -x² + 2x上x Î(-¥, 0]È[4, +¥)的部分.;

22. (1)n = 1时，g₁ (x₀) = x₀显然成立；假设n = k时g_k (x₀) = x₀成立，当n = k + 1时，g_k+1 (x₀) = f[g_k(x₀)] = f (x₀) = g₁(x₀) = x₀∴对一切n Î N, g_n (x₀) = x₀都成立；(2)由(1)稳定不动点x₀只须满足f (x₀) = x₀即可∴6x₀ - 6x₀² = x₀∴x₀ = 0或x₀ = 5/6; (3)由f (x) < 0∴x < 0或x > 1∴g_n (x) < 0Ûf [ g_n-1 (x)] < 0Ûg_n-1 (x) < 0或g_n-1 (x) > 1∴要使对一切nÎN且n > 2都有g_n (x) < 0，必须有g₁ (x) < 0或g₁ (x) > 1∴x < 0或x > 1或(3 -Ö3)/6 < x < (3+Ö3)/6∴对于区间((3 -Ö3)/6 , (3+Ö3)/6)和(1, +¥)内的任意x只要n > 2都有g_n (x) < 0.