2002年武汉市部分学校高中三年级调研测试
数学试题
2002.5.23～24
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。考试时间120分钟。
试题中注明文科做的，理科考生不做；注明理科做的，文科考生不做；未作注明的，文理科考生都做。
第Ⅰ卷（选择题，共60分）
注意事项：
1、答第Ⅰ卷前，考生务必将自己的姓名、考试科目、准考证号用铅笔涂写在答题卡上。
2、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。
3、考试结束，监考人员将本试卷和答题卡一并交回。
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）若非负整数
则n=
（A）0 （B）1
（C）2 （D）3
（2）在正方体
中，直线AC与
所成的角是
（A）90° （B）60°
（C）45° （D）30°
（3）[文科做]下列函数中，以π为周期且在区间（0，
）上为增函数的函数是
（A）
（B）y=-tgx
（C）y=sin2x （D）y=-cos2x
[理科做]在极坐标系中，已知圆ρ=2sinθ上一点P的极角为
，则点P的极径为
（A）
（B）
（C）
（D）
（4）设α，β都是第二象限的角，且sinα<sinβ，则
（A）tgα<tgβ （B）cosα<cosβ
（C）
（D）
（5）已知△ABC的三边a，b，c满足
，则△ABC是
（A）锐角三角形 （B）直角三角形
（C）最大角大于120°的钝角三角形
（D）最大角小于120°的钝角三角形
（6）设A是抛物线
上一点，B是点A关于x轴的对称点。若抛物线的焦点F为△AOB的垂心，则点A的横坐标为
（A）
（B）
（C）
（D）
（7）线段
、
分别是已知椭圆的长轴和短轴，
是椭圆的一个焦点
，若该椭圆的离心离为
，则
（A）30° （B）45°
（C）120° （D）90°
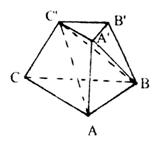
（8）如图，在三棱台A′B′C′-ABC中，已知上、下底面的面积分别是1和9，高是3，则
（A）5 （B）4
（C）3 （D）2
（9）方程
的两个根都是虚根，且两根的模的和为2，则实数m=
（A）
（B）2
（C）
（D）±2
（10）一批物资要用11辆汽车从甲地运到360千米外的乙地，若车速为v千米/时，则两车的距离不能小于
千米，运完这批物资至少需要
（A）10小时 （B）11小时
（C）13小时 （D）12小时
（11）若
是方程
的解，则
（A）（0.1,0.2） （B）（0.3,0.4）
（C）（0.5,0.7） （D）（0.9,1）
（12）用记号“
”表示求两个实数a与b的算术平均数的运算，即
。已知数列
满足
，
，
，则
（A）0 （B）
（C）
（D）1
第Ⅱ卷（非选择题，共90分）
注意事项
1、第Ⅱ卷3—6页，用钢笔或圆珠笔直接答在试题卷上。
2、答题前，将密封线内的项目填写清楚。
3、考试结束后，监考人将第Ⅱ卷密封装订成册。
二、填空题：本大题共4个小题，每小题4分，共16分。把答案填在题中横线上。
（13）圆台的轴截面的面积等于
，母线与底面所成的角为30°，则圆台有侧面积等于________
。
（14）设抛物线
的一条弦AB以点P（1，1）为中点，则该弦所在直线的斜率为___________。
（15）已知z=1，当arg（z-2i）取得最大值时所对应的复数z=_______。
（16）有A、B、C三台不同型号的数控车床，甲、乙、丙、丁四名操作员，其中甲、乙会操作这三种车床，丙不能操作车床C，丁只会操作车床A。今从四人中选三人分别去操作以上车床，不同的选派方案共有__________种。
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
（17）（本小题满分12分）
设数列
是公差不为0的等差数列，且
，
。
（Ⅰ）试求出这个数列的通项
；
（Ⅱ）将前n项的和
表示成关于的函数。
（18）（本小题满分12分）
已知函数f（x）=Asin（ωx+φ）（A>0，ω>0，
）的图象在y轴上的截距为1，它在y轴右侧的第一个最高点和最低点分别为（，2）和（
，-2）。
（Ⅰ）求f（x）的解析式；
（Ⅱ）若
，
，求
的值。
（19）（本小题满分12分）
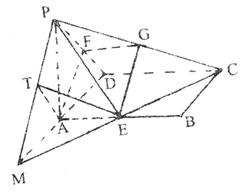
如图，四棱锥P-ABCD的底面是边长为4的正方形，高PA=3，E、F分别为AB、PD的中点。
（Ⅰ）求证：AF∥平面PCE；
（Ⅱ）求平面PAD和平面PCE所成角的正切值。
（20）（本小题满分12分）
设定义在实数集R上的函数
，
，f（x）满足
，且对区间D上的任意两相异实数
，
，恒有
。
（Ⅰ）若
是区间D上的增函数，能否确定y=f（x）是区间D上的增函数？
（Ⅱ）若
是区间D上的增函数，能否确定y=f（x）是区间D上的增函数？
在上述两问中，如果能够确定，请给出证明；否则，请举一反例。
（21）（本小题满分12分）
某进口产品，2001年的关税税率是100%，进口上岸价格是2000元（其中含1000元关税税款）。假如这种产品不含关税的价格因成本减少而按每年10%逐年降低，又因中国加入世贸组织后，该产品的关税税率将每年降低25%，一直到2005年降到0为止。
（Ⅰ）至少到哪一年，这种产品的进口上岸价格将不高于2001年进口上岸价格的一半？
（Ⅱ）在2011年，这种产品进口上岸价格是否可以不超过360元？
（22）（本小题满分14分）
设双曲线C的方程为
，
、是该双曲线的两焦点。
（Ⅰ）记平面上一点P到双曲线实轴、虚轴和右焦点的距离分别为P（x）、P（y）和
。问在双曲线C的右支上是否存在一点P，使P（x）是P（y）和的等比中项。如果存在，试求出点P的横坐标：如果不存在，请说明理由；
（Ⅱ）若Q是曲线C上任一点，从左焦点引
的平分线的垂线，垂足为M。试求点M的轨迹方程。
2002年武汉市部分学校高中三年级调研测试
数学试题参考答案及评分标准
一、选择题：每小题5分，满分60分
（1）B （2）B （3）D （4）B （5）C （6）A
（7）D （8）C （9）A （10）D （11）C （12）C
二、填空题：每小题4分，满分16分
（13）20π （14）2 （15）
（16）8
三、解答题：共6小题，满分74分
（17）（本小题满分12分）
解：（Ⅰ）∵的公差不为0，∴
，
∴
，∴
由
，得d=-2，……………………3分
又由
，得
. ……………………5分
∴
，
即
……………………7分
（Ⅱ）由（Ⅰ）得
， …………9分
∴
，
即
.……………………12分
（18）（本小题满分12分）
解：（Ⅰ）由已知条件，得A=2。………………2分
，解得T=4π，∴
。………………4分
把（0，1）代入解析式
，得
2sinφ=1，又，解得
。………………6分
∴
即为所求。…………………7分
（Ⅱ）由，，得
，
………………10分
∴
。…………12分
（19）（本小题满分12分）
证明：（Ⅰ）取PC的中点G，
连结FG，EG，…………2分
∵
，
，∴
，
∴四边形AEGF是平行四边形。
∴AF∥EG。 …………4分
又
，
，
∴AF∥平面PCE。………………6分
解：（Ⅱ）延长DA、CE相交于M，则PM是所求二面角的棱
过点A作AT⊥PM于T，连ET，………………8分
∵EA⊥AD，EA⊥PA，∴EA⊥平面PAD。
根根三垂线定理ET⊥PM，
∴∠ETA是所求二面角的平面角。………………10分
注意到EA=2，AM=AD=4，
.
∴
即所求二面角的正切值为
.…………12分
（20）（本小题满份12分）
解：（Ⅰ）能够确定。证明如下：………………1分
∵是区间D上的增函数，
∴对任意的，
，若
，恒有
又
∴
，……………………4分
∴
即
∴y=f（x）是区间D上的增函数。……………………7分
（Ⅱ）不能确定。……………………8分
令
是R上的增函数，对任意的两实数，，
满足
，
但
在R上是减函数。……………………12分
（21）（本小题满分12分）
解：（Ⅰ）已知第一年即2001年的进口上岸价格为2000元，则第n年的进口上岸价格为
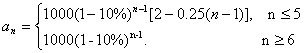…………4分
由此知
，
，
。
注意到随n的增加而减少，
故至少到2004年，这种产品的进口上岸价格将不高于2001年进口上岸价格的一半。
…………6分
（Ⅱ）[解法1]首先注意到，当5≤k≤9时，
.…………9分
∴
，
∴
.
故在2011年，这种产品的进口上岸价格不超过360元。………………12分
[解法2]假设在2011年这种产品的进口上岸价格可以超过360元，
则
，
即
，
亦即
，
∴
，
即
，
∴
.矛盾。
故在2011年这种产品的进口上岸价格不超过360元。……………………12分
（22）（本小题满分14分）
解：（Ⅰ）设双曲线右支上的点
满足题设要求。因为双曲线右准线方程为
，离心率为e=2。根据双曲线的准线性质
.……………………4分
又
，
.
根据题设要求，得
，
整理得
，
解之
，
。
即所求的点P存在，其横坐标为
.……………………7分
（Ⅱ）若Q在双曲线的右支上，则延长
到T，使
；
若Q在双曲线的左支上，则在上取一点T，使。
根据双曲线的定义
，所以点T在以
为圆心，2为半径的圆上，即点T的轨迹方程是
① ………………………………11分
由于点M是线段
的中点，设M（x，y），
，
则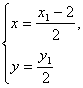
即
代入①并整理得点M的轨迹方程为
.……………………14分