湖北省2002届
鄂南高中 华师一附中 黄冈中学 黄石二中
荆州中学 孝感高中 襄樊四中 襄樊五中
八校联考
数学试卷（文）
命题人：黄冈中学 曾建民
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分。考试时间120分钟。
第Ⅰ卷（选择题 共60分）
参考公式：三角函数的积化和差公式
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案填在答题卡中。
1．已知函数
，则f(1)的值为
（ ）
A．
B．1
C．
D．2
2．若
，则下列不等式恒成立的是
（ ）
A．
B．
C．
D．
3．若使集合
中有且只有一个元素的所有α的值组成集合N,则
A．N={-1，1}
B．N={0，1}
C．
D．
4．等差数列
的前n项的和为
，若
，则
等于
A．18 B．36 C．54 D．72
5．若复数
，则复数
的辐角主值为
A．40° B．80° C．260° D．310°
6．若
，且
，则下列结论正确的是
A．
B．
C．
D．
7．从正方体的棱和各个面上的对角线中选出k条，使得其中任意两条线段所在的直线都是异面直线，则k的最大值为
A．2 B．3 C．4 D．6
8．无穷等比数列的前n项和为，若
，且
，则
A．
B．2
C．4
D．8
9．将
按二项式定理展开，则第4项为
A．
B．
C．60
D．-60
10．已知正数a、b满足a+b=1，则
的最小值为
A．5 B．9 C．11 D．16
11．已知
的图像如图甲，则函数
在[0，π]的大致图象为
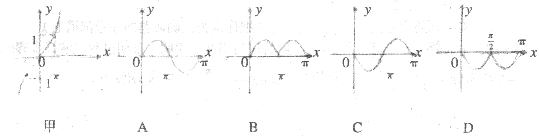
12．定义在R上的偶函数，满足
，且在区间[-1，0]上单调递增，设
，则
A．a<b<c B．c<a<b C．b<c<a D．c<b<a
第Ⅰ卷答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
注意事项：第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中，答卷前将密封线内的题目填写清楚。
| 题号 | 一 | 二 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 分数 |
第Ⅱ卷（非选择题90分）
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中的横线上。
13．设函数
的反函数为
，则函数
的定义域为_____
___________________。
14．
的值是______________________。
15．从6名优秀学生中选4名，分别担任班长、团支书、学习委员、体育委员四种班干职务，已知6人中的甲、乙不能担任体育委员，则不同的安排方案有___________种。（用数字作答）
16．关于复数
，有下列命题：
①复数
的辐角主值是α；
②复数z在复平面上对应点的轨迹是单位圆；
③
一定是实数；
④将复数z在复平面内对应的向量
按顺时针方向旋转90°得向量
，则对应的复数是
。
其中正确命题的序号是___________（把你认为正确命题的序号都填上）。
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。
17．（本小题满分12分）已知z是复数，且
，求复数z。
18．（本小题满分12分）已知
，若对于任意的实数x恒有
成立，求a的取值范围。
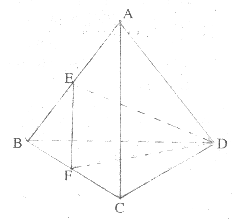
19．（本小题满分12分）已知正三棱锥A—BCD的底面边长为a，E、F分别为AB、BC的中点，且AC⊥DE。
（Ⅰ）求此正三棱锥的体积V；
（Ⅱ）求二面角E—FD—B的正弦值。
20．（本小题满分12分）数列的前n项和
且
，
（Ⅰ）求数列的首项
及常数p的值；
（Ⅱ）若
，用a表示
，并由此求数列的通项公式。
21．（本小题满分12分）某企业实行裁员增效，已知现有员工a人，每人每年可创纯收益（已扣工资等）1万元，据评估在生产条件不变的条件下，每裁员一人，则留岗员工每人每年可多创收0.01万元，但每年需付给下岗工人0.4万元的生活费，并且企业正常运转所需人数不得少于现有员工的
，设该企业裁员x人后年纯收益为y万元。
（Ⅰ）写出y关于x的函数关系式，并指出x的取值范围：
（Ⅱ）当
时，问该企业应裁员多少人，才能获得最大的经济效益。
（注：在保证能取得最大经济效益的情况下，能少裁员，应尽量少裁）
22．（本小题满分14分）定义在区间（-1，1）上的函数
满足：
1）对任意的
都有
；
2）当
时，
。
（Ⅰ）求证为奇函数；
（Ⅱ）试解不等式
。
湖北省2002届八校联考数学试卷（文）参考答案及评分标准
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | D | D | C | C | C | D | A | B | A | B |
二、填空题：
| 题号 | 13 | 14 | 15 | 16 |
| 答案 |
|
| 240 | ③④ |
三、解答题：
17．解：设复数
的模为
。则
，
∴
………………………………………………………………………4分
∵
，∴
，即
…………………………8分
∵
，∴
，∴
故所求复数
………………………………………………………………………………………12分
18．解：∵
（φ为一定角,大小与α有关）…………………………………………………………………………4分又∵
。
由，得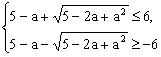
…………………………………………………8分
即
∴
。故所求α的取值范围是
，…………………………………………12分
19．解：（Ⅰ）作AO⊥平面BCD于O，由正三棱锥性质可知O为底面中心，连CO，则
CO⊥BD，……………………………………………………………………………………2分
由三垂线定理可知AC⊥BD，又AC⊥ED，∴AC⊥平面ABD，∴AC⊥AD，AB⊥AC，
AB⊥AD。……………………………………………………………………………………4分
在Rt△ACD中，由
可得
，∴
，
∴
………………………………………………6分
（Ⅱ）过E作EG⊥平面BCD于G，过G作GH⊥FD于H，连EH，由三垂线定理知EH⊥FD，即∠EHG为二面角E—FD—B的平面角。…………………………………………8分
∵
，而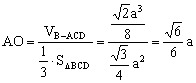
，∴
又∵
。
而EF∥AC，∴EF⊥DE ∴在Rt△FED中，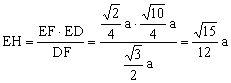
∴在Rt△EGH中，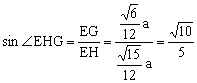
。即所求二面角的正弦值为
。
…………………………………………………………………………………………12分
20．（文）解：（Ⅰ）令
，则
……………2分
又令
，即
即
，∵
，∴
………………4分
（Ⅱ）令
，则
，即
，
同理，可得
。由此猜想
。………………………………6分
下面用数学归纳法证明：（1）当时，
，猜想正确。
（2）当时，
，猜想正确。（3）假设
时，猜想正确，即
。又
，∴
，当
时，猜想仍成立，综上可知：数列的通项公式为。…12分
21．解：（Ⅰ）由题意可得
。…4分∵
，即x的取值范围是
……………………………………6分
（Ⅱ）∵
，………………………………8分
又∵，所以
，故，当a为偶函数时，取
时，y取最大值；当a为奇数时，取
时y取最大值（为尽可能少裁，舍去
）………………………………………………………………………………11分
答：当员工为偶数人时，裁员
人，才能获得最大的经济效益；当员工为奇数人时，裁员（
）人时，才能获得最大的经济效益。…………………………………12分
22．解：（Ⅰ）令x=y=0，则
……2分
又令
，则
，而
，
∴
，即在（-1，1）上奇函数…………………………………4分
（Ⅱ）令
，则
，
，于是
即
，所以在定义域上为减函数……………………………………………………………………………………7分
从而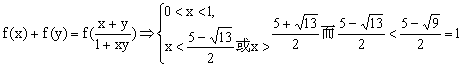
，
故所求不等式的解集为
…………………………………………12分