哈三中高三阶段考试数学试卷
一、选择题：（本大题共15小题，每小题4分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。）
参考公式：
正棱台、圆台的侧面积公式：
1．设双曲线
，（a>0，b>0）的一条准线与两条渐近线交于A、B两点，相应焦点为F，若以AB为直径的圆过点F，则双曲线离心率为（ ）
A．
B．
C．2 D．
2．要使
成立，则有（ ）
A．x-y≤0 B．x+y≤0 C．x-y≥0 D．x+y≥0
3．设t=sinα+cosα，且
，则t的取值范围是（ ）
A．
B．
C．
D．
4．设
成等差数列，
成等比数列，则
的取值范围是（ ）
A．[4，+∞） B．（-∞，0）∪[4，+∞）
C．[0，4） D．（-∞，-4）∪[4，+∞）
5．已知数列
的通项
（n∈N），则数列的前30项中最大项是（ ）
A．
B．
C．
D．
6．不等式
（a>0）的解集是（ ）
A．
B．
C．
D．{x0≤x≤a}
7．在棱长为a的正方体
中，P，Q是对角线
上的点，且
，则三棱锥P-BDQ的体积为（ ）
A．
B．
C．
D．不确定
8．函数y=asinx-bcosx的一条对称轴方程是
，则直线ax-by+c=0 的倾斜角为（ ）
A．
B．
C．
D．
9．已知P为椭圆
在第三象限内一点，且它与两焦点连线互相垂直。若点P到直线4x-3y-2m+1=0的距离不大于3，则实数m的取值范围是（ ）
A．[-7，8]
B．
C．[-2，2] D．（-∞，-7）∪[8，+∞）
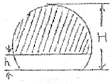
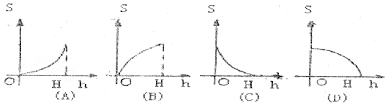
10．阴影部分面积S是h的函数（0≤h≤H），则该函数的大致图象是（ ）
11．三棱锥A-BCD的棱长全相等，E是AD的中点，则直线CE与BD所成角的余弦值为（ ）
A．
B．
C．
D．
12．设
，且sinα+sinγ=sinβ，cosα-cosγ=cosβ则β-α等于（ ）
A．
B．
C．
D．
二、填空题（本大题共有4个小题，每小题4分，共16分）
13．已知点P（m，n）在直线
上移动，其中a，b，c为某一直角三角形的三条边长，c为斜边，则
的最小值是__________________。
14．已知数列的前n项和
满足
（b>0，b≠1），则
的值等于__________________。
15．给出下列函数：
①函数
（a>0，且a≠1）与函数
（a>0，且a≠1）的定义域相同；
②函数与
的值域相同；
③函数
与
均是奇函数；
④函数
与
在
上都是增函数。
其中正确命题的序号是_____________（把你认为正确的命题的序号都填上）
16．点P与两个定点
（a>0）连线的斜率之积为常数k，当点P的轨迹是离心率为2的双曲线时，k的值为_____________。
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。）
17．（本小题满分12分）
解关于x的不等式
18．（本小题满分12分）
有两个各项都是正数的数列
，若对于任意自然数n都有
成等差数列，
成等比数列，
①求证：数列
是等差数列；
②如果
，记数列
的前n项和为，求
。
19．（本小题满分12分）
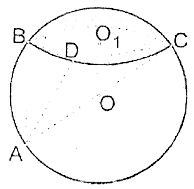
球O的截面BCD把球面面积分为1：3两部分，截面圆
的面积为12π，BC是截面圆的直径，D是圆上不同于B，C的一点，CA是球O的一条直径。
①求证：平面ADC⊥平面ABD；
②求三棱锥A-BCD的体积最大值；
③当D分
的两部分的比
时，求二面角B-AC-D的正切值。（球冠面积公式：s=2πRh）
20．（本小题满分12分）
甲、乙容器中有浓度分别为25%和75%的盐酸溶液各8克，从甲容器中倒出4克溶液倒入乙容器摇匀后，再从乙容器倒入甲容器4克溶液为一次操作，这样的操作反复进行。
①求第一次操作后，甲容器和乙容器中纯盐酸分别为多少克？
②求第n次操作后，甲容器和乙容器中纯盐酸分别为多少克？
③欲使两容器的浓度差小于1%，则至少操作多少次？
21．（本小题满分12分）
对于函数f(x)，若存在
，使
成立，则称
为f(x)的不动点。
已知函数
（a≠0）。
①当a=1，b=-2时，求函数f(x)的不动点；
②若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围；
③在②的条件下，若y=f(x)图象上A，B两点的横坐标是函数f(x)的不动点，且A，B两点关于直线
对称，求b的最小值。
22．（理科学生作）（本小题满分14分）
双曲线中心在原点，焦点在x轴上；过右焦点
作斜率为
的直线交双曲线于P，Q两点，
为左焦点，若
，又PQ=8，求双曲线方程。
（文科学生作）双曲线
，过右焦点作斜率为的直线交双曲线于P，Q两点，为左焦点，若，求双曲线方程，并求此时PQ的弦长。
参考答案：
一、选择题
ADABB DABAB AD
二、填空题
4， 1或-1， ①③④， 3
三、解答题：
17．当0<a<1时，解集为φ，当a>i时，解集为（a，+∞）
18．
19．V=16，正切值为
20．4次
21．①3和-1 ②0<a<1 ③
22．（理）
（文）8