高三数学小练
【模拟试题】
一. 选择题
1. 
等于( )
2. 
均为锐角，
等于( )
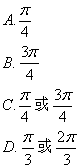
3. 等边
ABC顶点顺时针方向排列，若点A、B分别对应复数
，则顶点C对应复数为( )
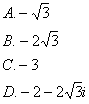
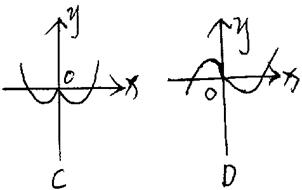
4. 函数
的部分图象是( )
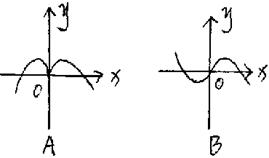
5. 一个等差数列共3n个项，其前2n个项之和为100，后2n个项之和为200，那么其中间n个项之和为( )
A. 150 B. 125 C. 75 D. 50
6. 以原点为顶点、椭圆C：
的左准线为准线的抛物线交椭圆C右准线于P、Q两点，则PQ等于( )
A. 2 B. 4 C. 8 D. 16
7. 直线
的倾斜角的取值范围是( )(其中
)
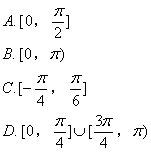
8. 圆台的上、下底面半径分别为r与R，高为h，且r：R：h＝1：4：4，那么此圆台侧面展开图扇环的圆心角的大小等于( )
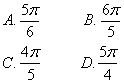
二. 填空题
9. 若抛物线的焦点为F(2，1)，准线L的方程为
，则其顶点M的坐标为__________。
10. 已知x，y为正实数，且
依次成等差数列，
依次成等比数列，那么
的取值范围是___________________。
三. 解答题
11. 设数列
的前n项和为
，若
是各项均为正数的等比数列，试比较
的大小，并加以证明。
12. 已知A、B是抛物线
上两个不同于原点的动点，若
，
于M，求动点M的轨迹方程，并说明它表示什么曲线。
【试题答案】
一.
1. D 2. B
3. C 4. D
5. C 6. D
7. D 8. B
提示：
1. 
2. 
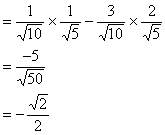
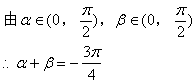
值得注意的是此条件下不宜计算
3. 向量
对应复数：
对应复数：
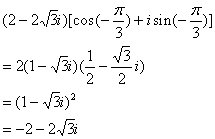
C点对应复数：
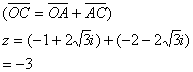
值得注意的是，若能熟练而准确地作图，则答案一目了然，要理解复数的二维性，对应二维空间的一个点，形数结合好，可以迅捷求解。
4. 提示：是奇函数，图象只能为B、D之一，考虑x由正实数趋于0时，
趋于负值，故选D。
5. 令n＝1，则
，由
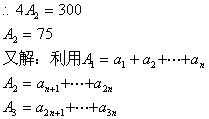
构成等差数列
6. 提示：利用椭圆的对称性，抛物线定义及通径概念；
7. 提示：式中
角并非直线倾角，而直线斜率
，画图并参照直线倾角取值[0，
)可进一步形数结合确定答案为D。
8. 如图示：
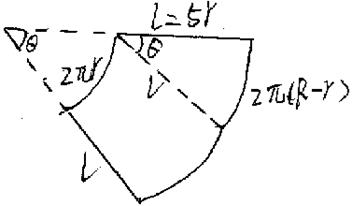
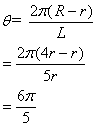
二. 填空题
9. 如图：
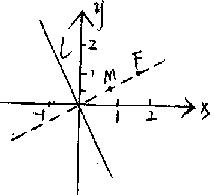
10.
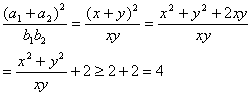
这里用到若
，则在等差数列中有
；在等比数列中有
；以及消元思想并综合均值定理的运用。
三. 解答题
11. 解：由已知，可设
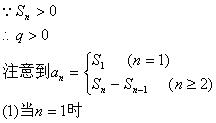
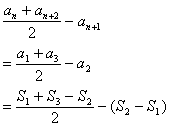
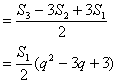
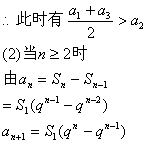
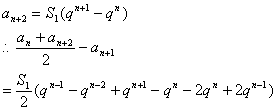
说明：此题综合考查数列通项
与前n项和之间关系，及运用差比较法证明不等式的能力，代数恒等变形能力，分情况讨论的方法。
其中：
当q>1时，k>0，
为增函数，结合函数，如图：
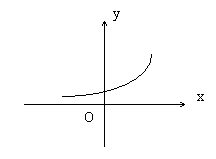
为凹函数。
有
性质
当q＝1，0<q<1可类似作深层分析，以提高对题目背景知识的认识，并进一步理解本题立意。
12. 解：如图：设直线OA方程为y＝kx。
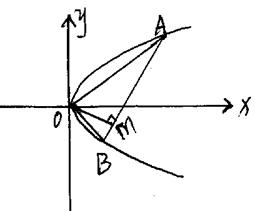
同理由方程组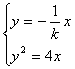
可解得B点坐标为
由点斜式可得直线AB方程为
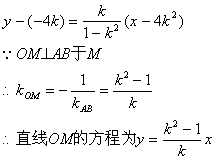
由动点M为直线AB与OM之交点
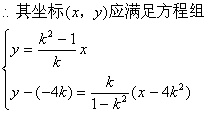
将组中两方程左、右两端分别相乘，可得方程
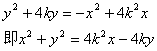
这接近圆方程，据题意结合图形可分析出圆心应在抛物线的对称轴上，可能在消去y的一次项的同时消去参数
据此，将直线OM方程
代入得
此动点轨迹乃圆心在C(2，0)点半径R＝2的圆(除去原点O)
说明：本题为2000年北京、安徽春季高校招生试题（文科），此法为编者所作，此外还有试卷评分答案及其它数学刊物（中学版）五、六种不同解法，感兴趣同学可自己从不同角度加以探求，例如角参数法，设点法等等，就不在此一一赘录了。
应该明确指出的是：解析几何综合题，是近年高考数学试卷的重要解答题之一，并常放在压轴题的位置上，原因是通过此种题目可以较全面、较深入地考查考生的数学能力，解析几何是用坐标法、代数方法来研究几何图形（主要是几种常见曲线）的数学分支、学习解析几何的知识水平及数学能力如何，对进一步学习高等数学有着极为重要的意义和作用。可以具体考查考生对数与形的沟通理解能力，设置恰当的参数，构建合理的方程组的能力，解方程组、对繁杂多变量代数式的恒等变形能力、运算能力、蕴含在计算中的分析与推理能力以及灵活运用平面几何知识，函数知识，不等式知识于解解几何问题的解答与化简能力等等，通过复习务必由简到难，由浅到深，有步骤，有意识地进行训练，积累，总结，以期不断有所提高。