高三数学上学期练习(5)

高三数学练习 (5)

2002.9　　　　　　　　 班级：___________, 姓名：______________,成绩：____________

一 .选择题：(每小题4分，共4×12 = 48分) 将答案填入下表中

1	2	3	4	5	6	7	8	9	10	11	12

y

y

y

　 1. 在以下四个按对应的函数关系式画出的略图中,不正确的是

x

x

x o

o x o

y

 

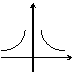
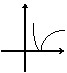
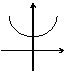
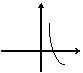
　　 (A)y=log₂x (B) y=2 ^x　　　　 (C) y=log_0.5 x²　　　(D) y= x   

　 2. 若0 < a < 1, b <－1，则函数f (x) = a^x + b的图象不经过
　　　 (A) 第一象限　　(B) 第二象限　　(C) 第三象限　　(D) 第四象限

　 3. 幂函数f (x)的图象过点(2,)，则f^-1 (4)的值是
　　　(A) 16　　(B) 　　(C) 　　(D) 2

　 4. 若0 < a < b < 1，则a^b, log_ba, logb的大小关系是
　　　(A) logb<a^b<log_b a (B) logb<log_b a<a^b (C) log_b a<logb<a^b (D)a^b<logb<log_b a

　 5. 已知函数f (x) = 2^x－1, g (x) = 1－x²，函数F (x)定义如下：当f (x) > g (x)时，F (x) =
　　 f (x) ；当f (x) < g (x)时，F (x) =－g (x)，那么F (x)

　　　(A)有最小值0, 无最大值　 　　(B)有最小值－1, 无最大值
　　　(C)有最大值1, 无最小值　　　 (D)无最小值也无最大值

　 6. 当0<x<1时 ,函数f (x)= x 与其反函数y= f ^-1 (x)之间对应函数值的大小关系是

　　　(A) f (x)>f ^-1 (x)　 (B) f (x) = f ^-1 (x)　 (C) f (x)<f ^-1 (x)　 (D)其大小要由x值确定

　 7. 函数f (x)= log_sin3 x²－6x +5 的单调递增区间是

　　　(A) (－, 3 ]　 (B) ( 1 , 3 ), (5 ,+)　 (C) [ 3 , +)　 (D) (－ , 1 ), ( 3 , 5 )

　 8. 已知x₁­是方程x + lgx = 3的根，x₂是方程x + 10^x = 3的根，那么x₁ + x₂的值为
　　　(A) 6　 (B) 3　 (C) 2　 (D) 1

　 9. 设函数f (x)=－2x² +3tx +t (x,tR)的最大值是u(t), 当u(t)有最小值时, t的值等于

　　　(A)　 (B)－　 (C)　　(D)－　

　 10. 若x, y是方程t²－2at+a+6=0的两个实根, 则(x－1)²＋(y－1)²的最小值是

　　　(A)－　 (B) 18　 (C) 8　 (D)不存在　

　 11. 若二次函数f (x) = 4x²－2(p－2)x－2p²－p + 1在区间[-1, 1]内至少存在一点C (c, 0)，
　　　 使得f (c) > 0，则实数p的取值范围是
　　　(A) -< p < 1　　(B) -3 < p <　　(C) p < -3　　(D) -3 < p < -或1 < p <

　 12. 定义在R上的函数f(x)对于任意两个不等的实数a,b总有成立，则一定有
　　　(A) f(x)是偶函数(B) f(x)是奇函数 (C) f(x)是R上的减函数 (D)f(x)是R上的增函数

二 .填空题：(每小题5分，共5×8 = 40分)

　 13 .已知log₁₂ 27 = a，则log₆ 16 = ________________ .(用a表示)　　

　 14 .比大小：()________();1.6________0.6^－;log3__________log2 .

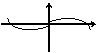　 15. 已知函数y = ax³ + bx² + cx + d的图象如图所示，用“>”, “<”, “=”　
　　　连接：a________0, b________0, c_______0, d________0　.

　 16. 若x> -1, 则f (x)=x² +2x +的最小值为____________ .

　 17. 已知f (x)是定义在R上的奇函数，当x < 0时f (x) = ()^x，那么f ()的值为_____ .

　 18 .方程= 3的解是________________ .

　 19 .方程log₂ (x－3) = log₄ (5－x)的解集是_____________ .

　 20 .如果对数方程log_0.5 (x+)= a有解,则实数a的取值集合是________ .　

三 .解答题：(四小题共62分)

　 21. 设y = (log₂x)² + (t－2)log₂x－t + 1，若t在区间[-2, 2]上变动时，y的值恒正，试求x的取值范围.

　 22. 解关于x的方程：= 2.

　 23. 已知函数f (x) = x (kÎZ)满足f (2) < f (3). (1). 求k的值，并写出相应的函数f (x)的解析式；(2). 对于(1)中所求得的函数f (x)，试判断是否存在正数q，使函数g (x) = 1－qf (x) + (2q－1)x在区间[-1, 2]上的值域为[-4,]. 若存在，求出q的值；若不存在，说明理由.

　 24. 设f (x)是定义在R上以2为周期的周期函数,且是偶函数.在区间[2,3]上f (x)=－2(x－3)²+4 . (1) 求x[ 1 , 2 ]时,f (x)的解析表达式 ;(2) 若矩形ABCD的两个顶点A,B在x轴上,另两个顶点C,D在函数y=f (x) (0x2)的图象上,求这个矩形面积的最大值 .

答案：二.13. 12-4a/(3+a); 14. <;<;< ;15. <,=,>,=; 16. 3³Ö2/2－1;17. -Ö3; 18. -1;19.{4};20. (-,0] .

三. 21. 提示：令f (t) = (log₂x-1)t + (log₂x-1)², 由f (-2) > 0且f (2) > 0解得0 < x < 1/2或x > 8;

22.提示：a < -1/4 or a = 0时，方程无解；a = -1/4时，方程有一解x = 1/4；-1/4 < a < 0时，方程有两解x = [2a+1±Ö(4a+1)]/2；a > 0时，方程有一解x = [2a+1+Ö(4a+1)]/2;
23. 提示：(1)k =0, 1时均有f (x) = x²; (2)若存在q > 0, 则g (x) = -qx² + (2q - 1)x + 1, xÎ[-1, 2], 其图象顶点(2q-1/2q, 4q²+1/4q) ∵ q>0∴2q-1/2q = 1-1/2q <1<2. 当2q-1/2q< -1, 即0<q<1/4时, g(x)_Max = g(-1)=2-3q, 令2-3q=17/8则q = -1/24<0矛盾; 当2q-1/2qÎ[-1, 1/2],即1/4<q<1时, g(x)值域[g(2),　4q²+1/4q]∴g(2) = -4且4q²+1/4q = 17/8∴-1 = -4且8q² - 17q + 2 = 0矛盾；当q > 1时2q-1/2qÎ(1/2, 2]∴g(x)值域[g(-1), 4q²+1/4q ]∴g(-1) = -4且4q²+1/4q =17/8解得q=2∴存在;
24. 提示: (1) f (x)=－2(x－1)² +4 (1x2) ;(2) 设A(1-x, 0), 则B(1+x, 0) (0<x<1)∴AB = 2x, AD = 4 - 2x²∴S = 2x(4 - 2x²) ∴S² = 4x²(4 - 2x²)² < [4x²+(4 - 2x²)+(4 - 2x²)]³/27 = 8³/27∴S_MaX=

1	2	3	4	5	6	7	8	9	10	11	12
C	A	C	A	B	C	D	B	D	C	B	D