多面体与旋转体 练习题
一. 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 一个长方体共一个顶点的三个面的面积分别为![]() ,这个长方体对角线的长是( )
,这个长方体对角线的长是( )
A. ![]() B.
B. ![]() C. 6 D.
C. 6 D. ![]()
2. 设正六棱锥的底面边长为1,侧棱长为![]() ,则此棱锥的体积为( )
,则此棱锥的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
3. 圆锥轴截面顶角为![]() ,那么它的侧面展开图扇形的圆心角为( )
,那么它的侧面展开图扇形的圆心角为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 已知圆台上、下底面半径分别为1,2,侧面积等于上、下底面积的和,那么该圆台的高为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 将一张圆形纸片沿其两条半径剪开,得到两个扇形,它们的圆心角的比为1:2,再将这两个扇形卷成两个圆锥筒(不计损耗和接缝用料),那么这两个圆锥筒的容积之比为
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
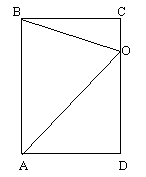
6. 设![]() 是矩形
是矩形![]() 的边
的边![]() 上一点,以直线
上一点,以直线![]() 为轴旋转这个矩形所得圆柱的体积为
为轴旋转这个矩形所得圆柱的体积为![]() ,其中以
,其中以![]() 为母线的圆锥的体积为
为母线的圆锥的体积为![]() ,则以
,则以![]() 为母线的圆锥的体积等于( )
为母线的圆锥的体积等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 若一个正方体所有顶点都在一个球面上,则该球与正方体的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 若干毫升水倒入底面半径为![]() 的圆柱形器皿中,量得水面高度为
的圆柱形器皿中,量得水面高度为![]() ,若将这些水倒入轴截面是正三角形的侧圆锥形器皿中,则水面的高度是( )
,若将这些水倒入轴截面是正三角形的侧圆锥形器皿中,则水面的高度是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 已知长方体的对角线长为![]() ,则长方体全面积的最大值是( )
,则长方体全面积的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 球面上三点,任意两点的球面距离都等于此球大圆周长的![]() ,若经过这三点的小圆面积为
,若经过这三点的小圆面积为![]() ,则该球的体积为( )
,则该球的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
11. 把边长为1的正方形![]() 沿其对角线
沿其对角线![]() 折起,使二面角
折起,使二面角![]() 为
为![]() ,那么三棱锥
,那么三棱锥![]() 的体积为( )
的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
12. 母线长为![]() 的圆锥体积最大时,其侧面展开图圆心角
的圆锥体积最大时,其侧面展开图圆心角![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二. 填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13. 正四棱锥底面边长为3,体积为![]() ,则它的侧面与底面所成角的大小为_______。
,则它的侧面与底面所成角的大小为_______。
14. 半径为![]() 的球内有二个平行截面,其面积分别为
的球内有二个平行截面,其面积分别为![]() ,那么这两个平行截面之间的距离为____________。
,那么这两个平行截面之间的距离为____________。
15. 把一个大金属球表面涂漆,共需油漆![]() 。若把这个大金属球熔化,制成64个大小都相同的小金属球,不计损耗,将这些小金属球表面都涂漆,需要用漆_________
。若把这个大金属球熔化,制成64个大小都相同的小金属球,不计损耗,将这些小金属球表面都涂漆,需要用漆_________![]() 。
。
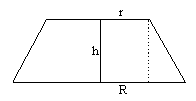
16. 圆台的母线与底面成![]() 角,侧面积为
角,侧面积为![]() ,则它的轴截面面积为___________。
,则它的轴截面面积为___________。
三. 解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17. (本小题满分12分)
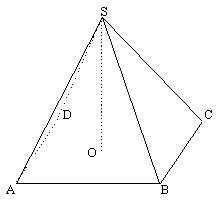
如图,![]() —
—![]() 是正四棱锥,高
是正四棱锥,高![]() ,相邻两侧面所成角为
,相邻两侧面所成角为![]() ,且
,且![]() ,求
,求
(I)侧棱与底面所成角的大小;
(II)侧棱和底面边长。
18. (本小题满分12分)
斜三棱柱![]() 的底面是边长为
的底面是边长为![]() 的正三角形,侧棱长为
的正三角形,侧棱长为![]() ,侧棱
,侧棱![]() 与底面两边
与底面两边![]() 所成的角都是
所成的角都是![]() 。求这斜三棱柱的侧面积。
。求这斜三棱柱的侧面积。
19. (本小题满分12分)
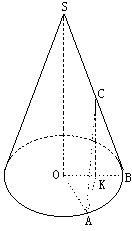
设![]() 是圆锥
是圆锥![]() 的两条母线,
的两条母线,![]() 是底面圆心,底面积为
是底面圆心,底面积为![]() 是
是![]() 中点,
中点,![]() 与底面所成角为
与底面所成角为![]() 。求这圆锥的体积。
。求这圆锥的体积。
20. (本小题满分12分)
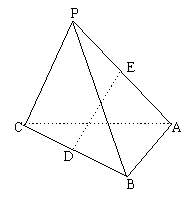
在三棱锥![]() 中,
中,![]() 和
和![]() 的公垂线段
的公垂线段![]() (如图)。求三棱锥
(如图)。求三棱锥![]() 的体积。
的体积。
21. (本小题满分12分)
圆台的侧面积为![]() ,它的侧面展开图为半圆环,圆台的上、下底面半径之比为1:3,求这圆台的体积。
,它的侧面展开图为半圆环,圆台的上、下底面半径之比为1:3,求这圆台的体积。
22. (本小题满分14分)
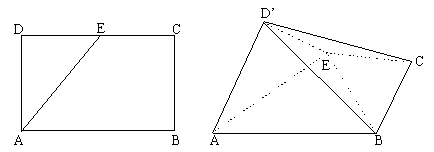
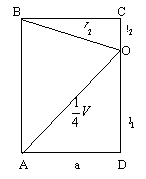
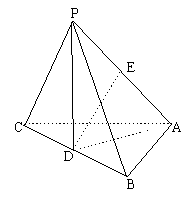
如图,![]() 是矩形,
是矩形,![]() 是
是![]() 中点。以
中点。以![]() 为棱,将
为棱,将![]() 向上折起,将
向上折起,将![]() 变到
变到![]() 位置,使面
位置,使面![]() 。
。
(I)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(II)求证:![]() ;
;
(III)求四棱锥![]() 的体积。
的体积。
试题答案:
一. 选择题:
1. D 2. C 3. D
4. B
提示:设圆台母线长为![]()
则![]()
故![]()
5. A
提示:两个扇形的圆心角分别为![]()
故两圆锥底面圆半径分别为![]() (其中设圆形纸片半径为1)
(其中设圆形纸片半径为1)
于是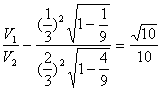 。
。
6. C
提示:如图并依题意有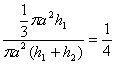
故![]()
![]()
7. C
提示:设球半径为![]() ,正方体棱长为
,正方体棱长为![]()
则![]()
即![]()
其体积比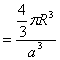
8. B
提示:利用水的体积相等,设水面高度为![]()
则![]() ,求
,求![]()
9. A
提示:设长方体过同一顶点的三条棱长为![]()
则![]()
![]()
当且仅当![]() 时取等号。
时取等号。
10. B
提示:设球半径为![]()
由已知可得,以球心为顶点,球面上三点组成的三角形为底面的三棱锥中,侧面顶角都为![]()
故球面上三点中,任意两点间距离为![]()
再由已知可得![]()
11. D
提示:取![]() 中点
中点![]() ,连结
,连结![]()
则![]()
12. A
提示:设圆锥底面半径为![]() ,则其体积
,则其体积
![]()
当且仅当![]()
即![]() 时,上式取等号
时,上式取等号
此时![]()
二. 填空题:
13. ![]()
14. ![]()
提示:注意球心可在两平行平面之间,也可在两平行平面同侧。
15. 9.6
提示:设大、小球半径分别为![]()
则由![]()
故![]()
又单位面积用漆量为![]()
![]() 共用漆
共用漆![]()
16. 3
提示:如图依题意有![]()
又![]()
![]()
即![]()
![]() 轴截面面积
轴截面面积![]()
三. 解答题:
17. (I)作![]() 于
于![]() ,连结
,连结![]()
由![]()
得![]()
即![]()
![]() 为两侧面所成二面角的平面角,为
为两侧面所成二面角的平面角,为![]() ,并且
,并且![]() 是侧棱与底面所成角,记作
是侧棱与底面所成角,记作![]() ,连结
,连结![]()
由![]()
故![]()
在![]() 中,
中,
![]()
![]()
![]()
即侧棱与底面所成角为![]()
(II)在![]() 中,
中,![]()
![]() 侧棱
侧棱![]()
![]() 底面边长
底面边长![]()
18. 由已知![]()
过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连结
,连结![]()
故![]()
![]()
于是![]()
从而![]()
![]() 是
是![]() 中
中![]() 的平分线
的平分线
又![]() 是正三角形
是正三角形
![]()
故![]()
![]() 是矩形,
是矩形,![]()
![]() 所求侧面积
所求侧面积![]()
19. 如图,作![]() 于
于![]()
![]()
![]()
从而![]()
连结![]() 为
为![]() 与底面所成二面角的平面角
与底面所成二面角的平面角
即![]()
又底面积为![]()
故底面半径为10
在![]() 中,可求得
中,可求得![]()
故![]()
![]()
20. ![]()
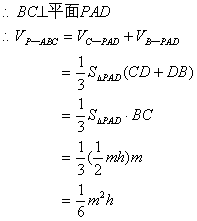
21. 设圆台上、下底面半径分别为![]() ,母线长为
,母线长为![]() ,高为
,高为![]()
则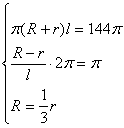
解得![]()
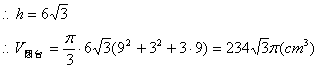
22. (I)作![]() 于
于![]() ,连结
,连结![]()
由面![]()
故![]()
![]() 是
是![]() 与面
与面![]() 所成角
所成角
![]() ,
,![]() 是
是![]() 中点
中点
故![]()
在![]() 中,可求得
中,可求得![]()
![]()
(II)在矩形![]() 中,连结
中,连结![]()
由![]()
![]()
即![]()
由(I),![]()
故![]()
![]()
又![]()
![]()
(III)![]()
![]()