西安市2002年高考分卷练习试题
数学（文史类）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟。
第Ⅰ卷（选择题共60分）
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型（A或B）用铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用像皮擦干净后，再选涂其它答案。不能答在试题卷上。
3．考试结束，监考人将本试卷和答题卡一并收回。
参老公式：
正棱台、圆台的侧面积公式
其中c′、c分别表示上、下底面周长、l表示斜高或母线长
台体的体积公式
其中S′、S分别表示上、下底面积，h表示高
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项有符合题目要求的。
1．已知I为全集，集M、N有M∩N=N，则（ ）
A．
B．
C．
D．
2．幂函数f(x)的图像过点
，则
的值是（
）
A．16 B．
C．
D．2
3．若双曲线的实轴长、虚轴长、焦距依次成等比数列，则双曲线的离心率为（ ）
A．
B．
C．
D．
4．若复数z=sin50°-lcos50°，则
为（
）
A．10° B．80° C．260° D．350°
5．已知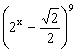
的展开式的第7项为
，则
的值是（
）
A．
B．
C．
D．
6．4个男生与3个女生站成一排，如果两端不站女生且3个女生必须相邻的排法有（ ）
A．144种 B．288种 C．432种 D．576种
7．正四棱锥P-ABCD的两个侧面PAB与PCD互相垂直，则相邻两个侧面所成二面角的平面角为（ ）
A．60° B．90° C．120° D．150°
8．设直线3x+4y-5=0的倾斜角为θ，则它关于直线x=3对称的直线的倾斜角是（ ）
A．
B．
C．π-θ
D．2π-θ
9．若x>0，y>0且
，则x+y的最小值是（ ）
A．6 B．12 C．16 D．24
10．使
为奇函数，且在
上是减函数的
的一个值是（
）
A．
B．
C．
D．
11．数列
的前n项和
，当n≥2时，有（ ）
A．
B．
C．
D．
12．如图，圆锥和一个球面相交，球心是圆锥的顶点，半径等于圆锥的高，若圆锥的侧面被球与圆锥的交线所平分，那么圆锥的母线与底面所成的角α等于（ ）
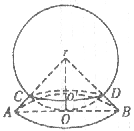
A．30° B．45°
C．60° D．75°
第Ⅱ卷（非选择题，共90分）
注意事项：
1．第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中。
2．答卷前将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
13．若
，则
=_______________。
14．若不等式
对一切实数x恒成立，则实数α的取值范围是_______________。
15．如图所示是一个正三棱柱的容器，高为2a，内装水若干，将容器放倒，把一个侧面作为底面，如图所示，这时水面恰好为中截面，请问图所示中水面的高度是_______________。
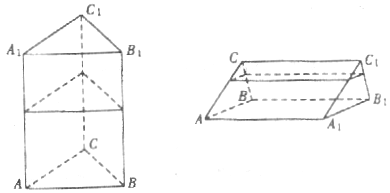
16．直线l过抛物线
的焦点且与x轴垂直，若l被抛物线截得的弦长为4，则a=_______________。
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
17．（满分12分）求值：
18．（满分12分）已知数列的前n项和为
对于n∈N，
总成等差数列。
（1）求通项
；
（2）计算
。
19．（本小题满分12分）
如图7，已知矩形ABCD中，AB=1，BC=a(a>0)，PA⊥平面ABCD
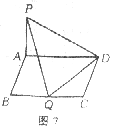
（1）问BC边上是否存在点Q，使得PQ⊥QD，并说明理由；
（2）若PA=1，且BC边上有且只有一个点Q，使得PQ⊥QD，求这时二面角Q-PD-A的大小。
20．（本小题满分12分）
天文台用3.2万元购买一台观测仪，这台观测仪从启用的第1天起连续使用，第n天的维修保养费为
元（n∈N），问这台观测仪使用多少天报废最合算？
21．（满分12分）
已知椭圆
，椭圆
的一个焦点
在
上，与对应的准线为x轴，（1）当在上移动时，证明的另一个焦点
的轨迹仍为椭圆；（2）若轨迹的长轴不超过10，求椭圆离心率的范围。
22．（满分14分）
已知二次函数
满足f(-1)=0，且对于任意x∈R都有
恒成立。
（1）求a、b、c的值；
（2）是否存在实数k使函数
有闭区间[-1，2]上递减？要详述其理由。
参考答案：
第Ⅰ卷（60分）
A
1．C 2．B 3．D 4．D 5．C 6．C 7．C 8．D 9．C 10．B 11．D 12．B
B
1．B 2．A 3．C 4．B 5．A 6．D 7．B 8．D 9．C 10．C 11．A 12．D
第Ⅱ卷（90分）
二、填空题：
13．
，X≥0
14．
15．
16．4
三、解答题：
17．（满分12分）
原式
…………………………4分
…………………………8分
…………………………10分
=……………………………………12分
18．（满分12分）
（1）
………………①
……………②
①—②：
，（n≥2）……………………4分
又由
∴
……………………6分
数列为首项为2，公比为
的等比数列
（n≥1）……………………8分
（2）数列是无穷递缩等比数列
∴
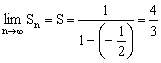…………………………12分
19．（1）由三垂线定理，得
∴当a>2时，BC边上两个点，即以AD为直径的圆与BC有两个交点，满足PQ⊥QD。………………2分
当a=2时，BC边上有中点，满足PQ⊥QD，当0<a<2时，BC边上不存在点Q，满足PQ⊥QD………………6分
（2）这时BC=2，Q是BC中点，
设G是AD中点，作GH⊥PD于点H，连结QH，GQ
由于PA⊥平面AC，则平面PAD⊥平面AC，因此QG⊥平面PAD，从而QH⊥PD，所以∠QHG是二面角的平面角……………………9分
在
中，
GQ=1，
…………………………12分
所求二面角的平面角大小是
……………………12分
20．（12分）
使用时期内平均每天耗费最低时，报废这种观测仪最合算，使用这台观测仪前n天的平均每天耗费为：
…………………………5分
=84.95（元）…………………………8分）
不等式取“=”的充要条件是
（n∈N），即n=800（天）……………………………………12分
答：这台观测仪使用800天最合算。
21．（12分）
（1）设
，椭圆的离心率为e，焦距为2C
…………………………2分
设的另一焦点
则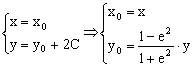
…………………………………………6分
代入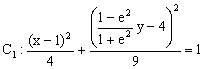
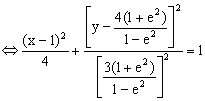
这是椭圆
（2）
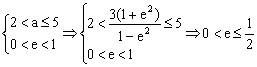…………………………12分
22．（14分）
（1）取x=1，得
∴f(1)=1 ∴a+b+c=1………………………………2分
又∵f(-1)=a-b+c=0
则
…………………………………………3分
由于
恒成立……………………4分
则：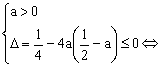
∴
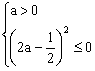………………………………6分
又由
得
，
………………………………8分
（2）由于
在[-1，2]上递减
所以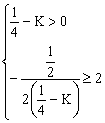
…………………………10分
或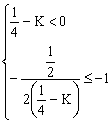
…………………………12分
角得K∈φ
不存在符合题意的实数K…………………………14分