数学综合练习(一)

综合练习 (三)

　　　　  班级：______________，姓名：___________________, 成绩：________________

一. 选择题：(每小题4分，共4×10 = 40分)将正确答案填入下表中

1. 已知集合M = {x -1 < x < 2}, N = {x x < a}. 若MN ¹ Æ，那么a的取值范围是
　　　(A) (-¥, 2]　　(B) (-1, +¥)　　(C) [-1, +¥)　　(D) [-1, 1]

2. a, bÎR，则 <成立的一个充分而不必要条件是

　　　(A) b < a < 0　 (B) a < b　 (C) ab(a－b) > 0　 (D) a > b　

3. 直线l₁ : x + y－3 = 0和斜率为且过点(－2,0)的直线l₂交于P点，又l₁与x, y轴分别交于P₁­, P₂点，则P分的比为
　　　(A) 2　 (B) 　 (C)－　 (D) 3

4. 下面有四个命题：①“直线a, b为异面直线”的充分不必要条件是“直线a, b不相交”；②“直线l^平面a内所有直线”的充要条件是“l^a”；③“直线a^b”的充分不必要条件是“a垂直于b在平面a内的射影”；④“直线a //平面a”的必要不充分条件是“直线a平行于平面a内的一条直线”. 其中正确命题的序号是
　　　(A)②③④　 (B) ②③　 (C) ①③　 (D) ②④

5. 复数z₁满足z₁ +－i £ 1，复数z₂满足z₂ = z₂－2 + 2i，那么z₁－z₂的最小值是
　　　(A) 　 (B)  + 1　 (C)  + 2　 (D) 3　

6. (理)函数y =  (£ x £)的值域是
　　　(A) [,]　 (B) [,]　 (C) [,]　 (D) [,]

　(文)设a, b > 0，且0 < a + b < p ，则y = sin(a + b)－(sina + sinb)的值是
　　　(A) 正数　 (B) 负数　 (C) 零　 (D) 非正数　

7. 已知{a_n}是等比数列，公比为q，设S_n = a₁ + a₂C+ a₃C+… + a_n+1C(其中n > 2, n Î N)，且S_n’ = C+C+…+C，如果存在，则公比q的取值范围是
　　　(A)－1 < q £ 1　(B)－1 < q < 1 (q ¹ 0)　(C)－3 < q < 1　(D)－3 < q £ 1 (q ¹ 0)

8. 将10个相同的小球全部装入3个编号为1、2、3的盒子中. 要求每个盒子中球的个数不少于盒子的编号数，则所有不同装法的种数是
　　　(A) 9　　(B) 12　　(C) 15　　(D) 18

9. 已知函数f (x) = ax² + bx + c (a, b, cÎR)对一切实数x, f (1－x) = f (1 + x)均成立，且f (－1) < 0,　　　

　　f (0) > 0，则有
　　　(A) c < 2b　 (B) abc > 0　 (C) a + b + c < 0　 (D) b < a + c　

10. 设F₁, F₂是椭圆的两个焦点，以F₁为圆心且过椭圆中心的圆与椭圆的一个交点为M. 若直线F₂M与圆F₁相切，则椭圆的离心率是
　　　(A) －1　　(B) 2－　　(C) 　　(D)

二. 填空题：(每小题4分，共4×4 = 16分)

11. 求值：= ___________________ .

12. 若(3x－1)ⁿ (nÎN)的展开式中各项系数和为128，则展开式中x²项的系数为__________ .

13. 已知OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得的曲面将圆锥分成体积相等的两部分，则母线与轴的夹角的余弦值为__________________ .　

14. 给出下列命题：①若0 < a <，则cos (1 + a) < cos (1－a)；②若0 < a < 1，则> 1 + a >；③若实数x, y满足y = x²，则log₂(2^x + 2^y)的最小值是；④若a, bÎR，则a² + b² + ab + 1 > a + b. 其中正确命题的序号是________________________ .

三. 解答题：(共44分)

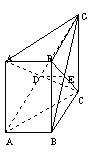
15. 在直三棱柱ABC－A₁B₁C₁中，底面ABC是直角三角形，ÐABC = 90°, 2AB = BC = BB₁ = a，且A_­1CAC₁ = D, BC₁B₁C = E，截面ABC₁与截面A₁B₁C交于DE. (1)求证：A₁C^BC₁；(2)求证：DE^平面BB₁C₁C；(3)设二面角D－BB₁－E为q，求tgq的值；(4)求三棱锥B₁－DEB的体积.

16. 在经济学中，函数f (x)的边际函数Mf (x)定义为：Mf (x) = f (x + 1)－f (x). 某公司每月最多生产100台报警系统装置，生产x台的收入函数R (x) = 3000x－20x² (单位：元)，其成本函数为C (x) = 500x + 4000 (单位：元)，利润是收入与成本之差. (1)求利润函数P (x)及边际利润函数MP (x)；(2) 利润函数P (x)及边际利润函数MP (x)是否具有相等的最大值？(3)你认为本题中边际利润函数MP (x)取得最大值的实际意义是什么？

17. 直线ax－y + 1 = 0与曲线3x²－y² = 1相交于A, B两点. (1)当a为何值时，以AB为直径的圆过原点；(2)是否存在这样的实数a使两交点A, B关于直线y = 2x对称.

18. 64个正数排成8行8列，如图所示. 在符号a_{i j} (1 < i < 8, 1 < j < 8)中，i表示该数所在的行数，j表示该数所在的列数. 已知每一行数都成等差数列，而每一列数都成等比数列且每列的公比q相等. 若a₁₁ =, a₂₄ = 1, a₃₂ =. (1)求a_{i j}的通项公式；(2)记第k行各项和为A_k，求A₁的值及A_k的通项公式；(3)若A_k < 1，求k的值.

参考答案：

一．

1	2	3	4	5	6	7	8	9	10
C	A	A	D	B	B	D	C	A	A

二. 11. Ö2/2; 12.- 189 ; 13. 1/⁴Ö2; 14.①②④;

三.15.(3)1/2; (4)V=a³/48;

16. (1)P (x) = R (x) - C (x) = -20x² + 2500x - 400 (xÎN且xÎ[1, 100]), MP (x) = 2480 - 40x (xÎN且xÎ[1, 100]); (2) ∵P (x) = -20(x - 125/2)² + 74125∴当x = 62或63时，P (x)有最大值74120. 又MP (x)是减函数∴x = 1时，MP (x)有最大值2440∴P (x)与MP (x)不具有相等的最大值；(3)MP (x)当x = 1时取得最大值说明生产第二台与生产第一台的总利润差最大，即第二台产品的利润最大. MP (x)是减函数说明随着产量的增加，每台利润与前一台利润比较，利润在减少.

17. (1)a = ±1; (2)不存在.

18.：(1)设第一行的公差为d，则a₂₄ = a₁₄q = (a₁₁ + 3d)q = 1, a₃₂ = a₁₂q² = (a₁₁ + d)q² = 1/4∴d = 1/2, q = 1/2∴a_{i j} = a_{1 j} q^{i - 1} = [a₁₁ + (j - 1)d]q^{i - 1} = j·(1/2)ⁱ; (2)A₁ = (1/2 + 4)·4 = 18, A_k = q^k-1 (a₁₁ + a₁₂ + … + a₁₈) = 36/2^k; (3) ∵A_k < 1∴36 < 2^k∴k = 6, 7, 8 .