2005学年度第一学期九校联考高三数学试卷 0512
一、 填空题（每小题4分，共48分）
1.
复数
___________.
2.
函数
的最小正周期是____________.
3.
函数
(x>0)的反函数是_____________.
4. 某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设, 其中甲同学必须被选派的概率是____________.
5.
已知
的反函数
图像的对称中心坐标是(0, 2), 则a的值为______________.
6.
不等式
解集为(1, +∞), 则不等式
的解集为___________.
7.
已知等差数列{an}前n项和为Sn. 若m>1, m∈N且
, 则m等于____________.
8. 将7名学生分配到甲、乙两个宿舍中, 每个宿舍至少安排2名学生, 那么互不相同的分配方案共有________种.
9.
函数
是定义在R上以3为周期的奇函数, 若
, 
. 则实数a的取值范围是________________.
10.
已知等差数列{an}公差不为0, 其前n项和为Sn, 等比数列{bn}前n项和为Bn, 公比为q, 且q>1, 则
=___________________.
11.
|
的图象如图所示，它在R上单调
递减，现有如下结论： 1
⑴
；⑵
；⑶
；⑷
。
0 1 x
其中正确的命题序号为______________.（写出所有正确命题序号）
12.
已知n次多项式
. 如果在一种计算中, 计算
(k=2,3,4,……, n)的值需要
次乘法, 计算
的值共需要9次运算(6次乘法, 3次加法). 那么计算
的值共需要__________次运算. 下面给出一种减少运算次数的算法: 
, 
, 利用该算法, 计算的值共需要6次运算, 计算的值共需要__________次运算.
二、选择题（每小题4分，共16分）
13.
集合
, 
, 则
( )
A. A={(1, 0)} B. {y0≤y≤1} C. {1, 0} D. φ
14.
设数列{an}前n项和
(A≠0, q≠0, q≠1) 则A+B=0是使{an}成为公比不等于1的等比数列的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件
D. 即不充分, 也不必要条件
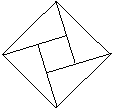
15. 2002年8月在北京召开了国际数学家大会, 会标如图示,
它是由四个相同的直角三角形与中间的小正方形拼成的
一个大正方形, 若直角三角形中较小的锐角为θ, 大正方
形面积是1, 小正方形面积是
, 则
的值是
( )
A. 1
B. 
C.
D. 
16. 2005年度大学学科能力测验有12万名学生, 各科成绩采用15级分, 数学学科能力测验成绩分布图如下图, 请问有多少考生的数学成绩高于11级分? 选出最接近的数目 ( )
A. 4000人 B. 10000人 C. 15000人 D. 20000人
三、解答题
17. (12分)
设复数
，
，
，求
的取值范围。
18. (14分)
命题甲: 
R, 关于x的方程
有两个非零实数解;
命题乙: R, 关于x的不等式
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
19.(12分)已知△ABC中，
，
求：角A、B、C的大小。
|
某地为了防止水土流失，植树造林，绿化荒沙地，每年比上一年多植相同亩数的林木，但由于自然环境和人为因素的影响，每年都有相同亩数的土地沙化，具体情况如下表所示：
| 2003年 | 2004年 | 2005年 | |
| 新植亩数 | 1000 | 1400 | 1800 |
| 沙地亩数 | 25200 | 24000 | 22400 |
而一旦植完，则不会被沙化。
问：⑴每年沙化的亩数为多少？
⑵到哪一年可绿化完全部荒沙地？
21.（16分）
设函数在
上满足
, 
且在闭区间[0, 7]上只有
.
⑴试判断函数
的奇偶性;
⑵试求方程
在闭区间
上的根的个数, 并证明你的结论.
a11，a12，……a18
22.（18分） a21，a22，……a28
……………………
64个正数排成8行8列, 如下所示： a81，a82，……a88
在符合
中，i表示该数所在的行数，j表示该数所在的列数。已知每一行中的数依次都成等差数列，而每一列中的数依次都成等比数列（每列公比q都相等）且
，
，
。
⑴若
，求
和
的值。
⑵记第n行各项之和为An（1≤n≤8），数列{an}、{bn}、{cn}满足
，联
（m为非零常数），
，且
，求
的取值范围。
⑶对⑵中的
，记
，设
，求数列
中最大项的项数。
2005学年度第一学期九校联考
高三数学试卷答案 2005.12.1
一、填空题
1、1; 2、π； 3、
（x>1）； 4、
； 5、
；
6、
； 7、10； 8、112； 9、
； 10、
；
11、⑵，⑶，⑷； 12、
；2n.
二、选择题
13、A； 14、C； 15、D； 16、B
三、解答题
17、略解：
18、解：当甲真时，设
，即两函数图象有两个交点.
则
当乙真时，
时 满足 或
也满足
则
∴当甲乙有但仅有一个为真命题时，即
或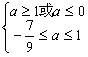
∴
19、解：
得
∴
∵
∴
又0<A<π
则
, 即
由得
即
亦即
∴
得
, 从而
′
则所求的角, , .
20、解：⑴∵每年都有相同亩数的土地被沙化
∴由表格可知，每年沙化的土地面积为
（亩）
⑵由⑴知，每年林木的“有效面积”应比实造面积少200亩。
设2005年及其以后各年的造林亩数分别为
，则几年造林面积总和为
由
得
即
∴到2012年可绿化完全部沙地。
21、解⑴由
∵在
上只有
∴
∴
故为非奇非偶函数。
⑵由
得 
∴是以10为周期的函数. 又
∴
∴在[0, 10]和
上各有2个根.
从而方程在
上有800个根, 而
上没有根,
在[2000, 2005]上有2个根.
故方程在上共有802个根.
22、解：⑴∵
，
∴
∵
成等差 ∴
⑵设第一行公差为d，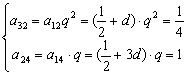 
解出：
，
′
∵
∴
∴
∵
∴
而
∴
∴
是等差数列
故
∵
∴
∴
⑶∵
是一个正项递减数列
∴
，
∴中最大项满足
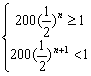
解出：6.643<n≤7.643
∵
, ∴n=7，即中最大项的项数为7项.