金山区2005学年度第一学期高三数学期末考试试题
(满分:150分,完卷时间:120分钟)
| 题号 | 1~12 | 13~16 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
|
|
|
|
|
|
|
|
|
| 签名 |
|
|
|
|
|
|
|
|
|
一、填空题(本大题共有12题,每题4分,满分48分)
1、已知集合A={xy=lg(x–3)},B={xy=![]() },则A∩B= 。
},则A∩B= 。
2、定义在R上的函数f(x)是奇函数,则f(0)的值为 。
3、设函数f(x)=lgx,则它的反函数f –1(x)= 。
4、函数y=sinxcosx的最小正周期T= 。
5、若复数z1=3–i,z2=7+2i,(i为虚数单位),则z2–z1= 。
6、ΔABC中,若∠B=30o,AB=2![]() ,AC=
,AC=![]() ,则BC=
。
,则BC=
。
7、无穷等比数列{an}满足:a1=2,并且![]() (a1+a2+…+an)=
(a1+a2+…+an)=![]() ,则公比q=
。
,则公比q=
。
8、关于x的方程2x=![]() 只有正实数的解,则a的取值范围是
。
只有正实数的解,则a的取值范围是
。
9、如果直线y = x+a与圆x2+y2=1有公共点,则实数![]() 的取值范围是 。
的取值范围是 。
10、袋中有相同的小球15只,其中9只涂白色,其余6个涂红色,从袋内任取2只球,
则取出的2球恰好是一白一红的概率是 。
11、F1、F2是双曲线![]() 的焦点,点P在双曲线上,若点P到焦点F1的距离等于9,则点P到焦点F2的距离等于 。
的焦点,点P在双曲线上,若点P到焦点F1的距离等于9,则点P到焦点F2的距离等于 。
12、对于集合N={1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对n=3、n=4的情况,计算它的“交替和”的总和S3、S4,并根据其结果猜测集合N={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和Sn= 。(不必给出证明)
二. 选择题(本大题共4题,每题4分,共16分)
13.已知数列{an}的通项公式是an=2n–49 (nÎN),那么数列{an}的前n项和Sn 达到最小值时的n的值是 ( )
(A) 23 (B) 24 (C) 25 (D) 26
14.在直角坐标平面中,若F1、F2为定点,P为动点,a>0为常数,则“PF1+PF2=2a”是“点P的轨迹是以F1、F2为焦点,以2a为长轴的椭圆”的 ( )
(A)充要条件 (B)仅必要条件 (C)仅充分条件 (D)非充分且非必要条件
15.设x=sina,且aÎ![]() ,则arccosx的取值范围是
( )
,则arccosx的取值范围是
( )
(A) [0, p] (B)
[![]() ,
,![]() ] (C) [0,
] (C) [0,![]() ]
(D) [
]
(D) [![]() ,p]
,p]
16.设非零实常数a、b、c满足a、b同号,b、c异号,则关于x的方程a .4x+b.2x+c=0( )
(A)无实根 (B)有两个共轭的虚根 (C)有两个异号的实根 (D)仅有一个实根
三、解答题(本大题共6题,共86分,解答下列各题必须写出必要步骤)
17.(本题满分12分)
过定点A(–1,1)是否存在直线l,使得点A恰为直线l与椭圆x2+3y2=9相交所得的线段的中点,若存在,请求出直线l的方程;若不存在,请说明理由。
18.(本题满分12分)
在复数范围内解方程![]() (i为虚数单位)
(i为虚数单位)
19.(本题满分14分)
已知不等式x2–3x+t<0的解集为{x1<x<m, mÎR}
(1)求t, m的值;
(2)若f(x)= –x2+ax+4在(–∞,1)上递增,求不等式log a (–mx2+3x+2–t)<0的解集。
20.(本题满分14分)
某企业准备在2006年对员工增加奖金200元,其中有120元是基本奖金。预计在今后的若干年内,该企业每年新增加的奖金平均比上一年增长8%。另外,每年新增加的奖金中,基本奖金均比上一年增加30元。那么,到哪一年底,
(1)该企业历年所增加的奖金中基本奖金累计(以2006年为累计的第一年)将首次不少于750元?
(2)当年增加的基本奖金占该年增加奖金的比例首次大于85%?
21.(本题满分16分)
已知Sn是正数数列{an}的前n项和,S12,S22、……、Sn2 ……,是以3为首项,以1为公差的等差数列;数列{bn}为无穷等比数列,其前四项之和为120,第二项与第四项之和为90。(1)求an、bn;(2)从数列{![]() }中能否挑出唯一的无穷等比数列,使它的各项和等于
}中能否挑出唯一的无穷等比数列,使它的各项和等于![]() 。若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由。
。若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由。
22.(本题满分18分)
函数f(x)=![]() (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立?为什么?
(3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P的距离AP的最小值。
金山区2005学年度第一学期高三数学期末考试试题
评分标准
一、填空题
1、{x3<x≤5} 2、0 3、y=10x, xÎR 4、p 5、5 6、3 7、![]() 8、
8、![]() <a<2
<a<2
9、–![]() ≤a≤
≤a≤![]() 10、
10、![]() 11、17 12、n .2n–1
11、17 12、n .2n–1
二、选择题
13、B 14、B 15、C 16、D
17、设过A点的直线交椭圆于B、C两点,B(x1, y1)、C(x2, y2)
则有x12+3y12=9,x22+3y22=9, …………………………………………………………3分
两式相减得:(x1+x2)( x1–x2)+3(y1+y2)( y1–y2)=0…………………………………………6分
因为A点是线段BC的中点,所以x1+x2= –2,y1+y2=2 ………………………………8分
代入得:kBC =![]() =
= ![]() ……………………………………………………………10分
……………………………………………………………10分
所以l的方程为y=![]() (x+1)+1……………………………………………………………11分
(x+1)+1……………………………………………………………11分
检验知:x–3 y+4=0为所求的方程。……………………………………………………12分
18、原方程化简为![]() ,………………………………………………3分
,………………………………………………3分
(只要写出右边1–i就得3分)
设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi=1–i, ………………………………5分
(只要写出左边就得2分)
所以x2+y2=1且2x = –1, ……………………………………………………………8分
(写对一个得2分)
解得x= –![]() …………………………………………………………………………9分
…………………………………………………………………………9分
y= ±![]() , …………………………………………………………………………11分
, …………………………………………………………………………11分
所以原方程的解是z= –![]() ±
±![]() i。…………………………………………………12分
i。…………………………………………………12分
19、(1) 由条件得:![]() ,………………………………………………………3分
,………………………………………………………3分
所以![]() ………………………………………………………………………………6分
………………………………………………………………………………6分
(2)因为f(x)=
–(x–![]() )2+4+
)2+4+![]() 在(–∞,1)上递增,
在(–∞,1)上递增,
所以![]() ≥1,a≥2 ………………………………………………………………………8分
≥1,a≥2 ………………………………………………………………………8分
log a (–mx2+3x+2–t)= log a (–2x2+3x)<0=log a 1
所以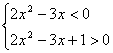 ,………………………………………………………………10分
,………………………………………………………………10分
所以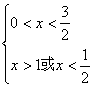 ……………………………………………………………………12分
……………………………………………………………………12分
所以0<x<![]() 或1<x<
或1<x<![]() …………………………………………………………………14分
…………………………………………………………………14分
20、(1)设基本奖金形成数列{an},由题意可知{an}是等差数列,(或a1=120,,d=30,或an =120+30 (n–1))…………………………………………………………………………1分
Sn=a1n+![]() n(n–1)d……………………………………………………………………2分
n(n–1)d……………………………………………………………………2分
则Sn=120n+15n(n–1) =15n2+105n=15(n2+7n)……………………………………………4分
注意:若直接写出Sn的整理式子(上面三个之一)4分全给
令15n2+105n≥750,即n2+7n–50≥0,而n是正整数, ∴n≥5。…………………5分
(不区分≥、>、=,这一结果只影响最终结果)
到2010年底该企业历年所增加的工资中基本工资累计将首次不少于750元。6分
(2)设新增加的奖金形成数列{bn},由题意可知{bn}是等比数列,(或b1=200,q=1.08,或bn=bn–1q) ………………………………………………………………………………7分
则bn=200· (1.08)n–1……………………………………………………………………9分
(在第2小题任意处出现上式,均给3分,即使b1=200,q=1.08,和bn=bn–1q同时出现,而没有代入,也给3分)
由题意可知an>0.85 bn,有120+30 (n–1)>200· (1.08)n–1·0.85。 …………………11分
(不区分≥、>、=,这一结果只影响最终结果)
由计箅器解得满足上述不等式的最小正整数n=5,………………………………13分
到2010年底,当年增加的基本奖金占该年增加奖金的比例首次大于85% ……14分
注意:如果直接列表计算也可,但表格必须完整,不能用……代替,否则第1小题只给2分,第2小题只给3分,对于表格中的数据,只要完整,不去验证具体数据。
21、(1){Sn}是以3为首项,以1为公差的等差数列;所以Sn2=3+(n–1)=n+2
因为an>0,所以Sn=![]() (nÎN)………………………………………………………2分
(nÎN)………………………………………………………2分
当n≥2时,an=Sn–Sn–1=![]() –
–![]()
又a1=S1=![]() ,所以an=
,所以an=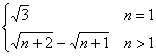 (nÎN) ……………………………4分
(nÎN) ……………………………4分
设{bn}的首项为b1,公比为q,则有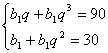 ………………………………6分
………………………………6分
所以![]() ,所以bn=3n(nÎN)…………………………………………………………8分
,所以bn=3n(nÎN)…………………………………………………………8分
(2)![]() =(
=(![]() )n,设可以挑出一个无穷等比数列{cn},首项为c1=(
)n,设可以挑出一个无穷等比数列{cn},首项为c1=(![]() )p,公比为(
)p,公比为(![]() )k,(p、kÎN), 它的各项和等于
)k,(p、kÎN), 它的各项和等于![]() =
=![]() ,……………………………………………………10分
,……………………………………………………10分
则有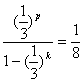 ,所以(
,所以(![]() )p=
)p=![]() [1–(
[1–(![]() )k],…………………………………………12分
)k],…………………………………………12分
当p≥k时3p–3p–k=8,即3p–k(3k–1)=8, 因为p、kÎN,所以只有p–k=0,k=2时,
即p=k=2时,数列{cn}的各项和为![]() 。 ……………………………………………14分
。 ……………………………………………14分
当p<k时,3k–1=8.3k–p,因为k>p右边含有3的因数,而左边非3的倍数,不存在p、kÎN,
所以唯一存在等比数列{cn},首项为![]() ,公比为
,公比为![]() ,使它的各项和等于
,使它的各项和等于![]() 。……16分
。……16分
22、(1)由f(2)=1得2a+b=2,又x=0一定是方程![]() =x的解,
=x的解,
所以![]() =1无解或有解为0,………………………………………………………3分
=1无解或有解为0,………………………………………………………3分
若无解,则ax+b=1无解,得a=0,矛盾,
若有解为0,则b=1,所以a=![]() 。 ……………………………………………………6分
。 ……………………………………………………6分
(2)f(x)=![]() ,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
取x=0,则f(0)+f(m–0)=4,即![]() =4,m= –4(必要性)……………………………8分
=4,m= –4(必要性)……………………………8分
又m= –4时,f(x)+f(–4–x)=![]() =……=4成立(充分性) ……………10分
=……=4成立(充分性) ……………10分
所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,…………11分
(3)AP2=(x+3)2+(![]() )2,设x+2=t,t≠0,…………………………………………13分
)2,设x+2=t,t≠0,…………………………………………13分
则AP2=(t+1)2+(![]() )2=t2+2t+2–
)2=t2+2t+2–![]() +
+![]() =(t2+
=(t2+![]() )+2(t–
)+2(t–![]() )+2=(t–
)+2=(t–![]() )2+2(t–
)2+2(t–![]() )+10
)+10
=( t–![]() +1)2+9,
…………………………………………………………………16分
+1)2+9,
…………………………………………………………………16分
所以当t–![]() +1=0时即t=
+1=0时即t=![]() ,也就是x=
,也就是x=![]() 时,
时,
AP min = 3 ………………………………………………………………………18分