黄冈中学06届高三数学第二轮专题训练(三)
命题人:黄冈中学高级教师 黄孝银
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.二项式 ![]() 的展开式中的常数项是
(
)
的展开式中的常数项是
(
)
A.15 B.-15 C.20 D.-20
2.已知![]() ,则
,则![]() 的值是
(
)
的值是
(
)
A.5 B.4 C.3 D.-3
3.已知a,b是两条不同的直线,α、β是两个不同的平面,且a垂直于平面α,b垂直平面β,则下面命题中的假命题是 ( )
A.若a平行于b,则α平行于β B.若α垂直于β,则a垂直于b
C.若a、b相交,则α、β相交 D.若α、β相交,则a、b相交
4.设函数f(x)是可导函数,并且![]() ,则
,则![]() (
)
(
)
A.![]() B.-1
C.0
D.-2
B.-1
C.0
D.-2
|
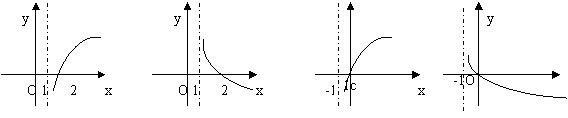
A B C D
6.过点P(-1,2)且方向向量为a=(-1,2)的直线方程为 ( )
A.2x+y=0 B.x-2y+5=0 C.x-2y=0 D.x+2y-5=0
7.如下图所示,A、B、C、D是某煤矿的四个采煤点,L是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形,已知A、B、C、D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的重量成正比,现要从P、Q、R、S中选出一处作为一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在 ( )

A. P点 B. Q点 C. R点 D. S点
8.设点P(x,y)在椭圆![]() 上,则点P到点(0,1)距离的最大值为
(
)
上,则点P到点(0,1)距离的最大值为
(
)
A.![]() B.3 C.2
D.
B.3 C.2
D.![]()
9.函数f(x)=![]() 的单调递增区间为(0,+∞),那么实数a的取值范围是
( )
的单调递增区间为(0,+∞),那么实数a的取值范围是
( )
A.a≥0 B.a>0 C.a≤0 D.a<0
10.从集合{1,2,3,4,5,6,7,8,9,10}中选出3个数组成的子集,使得这三个数中的任何两个数的和不等于11,这样的子集共有 ( )
A.120个 B.115个 C.75个 D.80个
11.在等比数列![]() 中,
中,![]() 则
则![]() 等于
(
)
等于
(
)
A.-1 B.1 C.-2 D.-2
12.正四面体ABCD中,G是△BCD的中点,M是AG上一点,若∠BMC=![]() ,则AM∶AG等于
( )
,则AM∶AG等于
( )
A.1∶1 B.1∶4 C.1∶3 D.1∶2
第Ⅱ卷(非选择题,共90分)
二、填空题(每小题4分,共4个小题,共16分)
13.设![]() 、
、![]() 是椭圆
是椭圆![]() 的两个焦点,P是椭圆上一点且且PF1-PF2=1,则
的两个焦点,P是椭圆上一点且且PF1-PF2=1,则
tan∠F1PF2=_________.
14.一个单位有职工160人,其中有业务员120人,管理人员24人,后勤服务人员16人,为了了解职工的身体健康状况,要从中抽取一定容量的样本,现用分层抽样的方法得到业务员的人数为15人,那么这个样本容量是_________.
15.一直角梯形ABCD,AD是垂直于上、下底的腰,AB=2,CD=1,BC=![]() ,E为AD的中点,沿CE、EB折成一个三棱锥E-ABC(缺一个面ABC),使A、D重合于A,则这个三棱锥的体积是________.
,E为AD的中点,沿CE、EB折成一个三棱锥E-ABC(缺一个面ABC),使A、D重合于A,则这个三棱锥的体积是________.
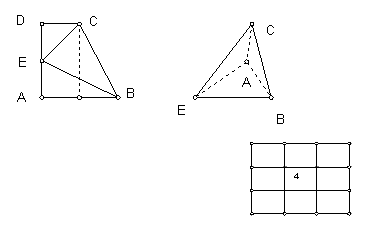 |
16.把数字1,2,3……,9这9个数字填写在如右图的9个空格
中,要求每一行从左到右依次增大,每列从上到下也依次增大,
当数字4固定在中心位置时,则所有填写空格的方法共有__________.
三、解答题(共74分)
17.(12分)在△ABC中,a,b,c分别是角A、B、C的对边,且
![]() .
.
(1)求角A的大小;
(2)若a=![]() ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
|
(1)判断四边形ABFE的形状并证明;
(2)求异面直线BD和CP所成的角;
(3)判断△MNP的形状并证明.
19.(12分)平面上有两个质点A、B分别位于点(0,0)、(2,2),在某一时刻同时开始每一秒钟向上下左右任一方向移动1个单位.已知质点A向左、右移动的概率都是![]() ,向上、下移动的概率分别是
,向上、下移动的概率分别是![]() 和
和![]() ,质点B向各个方向移动的概率都是
,质点B向各个方向移动的概率都是![]() . 试求:
. 试求:
(1) 点A经过2秒钟到达点C(1,1)的概率;
(2)A、B经过3秒钟,同时到达D(1,2)的概率.
20.(12分)已知x∈R,奇函数f(x)=x3-ax2-bx+c在[1,+∞]上是单调函数.
(1)求a、b、c应满足的条件;
(2)设x0≥1,f(x0)≥1且满足f(f(x0))=x0,求证:f(x0)=x0.
21.(12分)设x,y∈R, i、j为直角坐标平面内x、y轴正方向上的单位向量.若向量a = x
i + (y + ![]() )j, b= x i + (y -
)j, b= x i + (y -![]() )j, 且 a + b =4.
)j, 且 a + b =4.
(1)求点M(x,y)的轨迹C的方程;
(2)过点Q(-2,0)作直线L与曲线C交于A、B两点,设P是过点(![]() ,0)且以j为方向向量的直线上一动点,满足
,0)且以j为方向向量的直线上一动点,满足![]() (O为坐标原点),问是否存在这样的直线L,使得四边形OAPB为矩形?若存在,求出直线L的方程;若不存在,请说明理由.
(O为坐标原点),问是否存在这样的直线L,使得四边形OAPB为矩形?若存在,求出直线L的方程;若不存在,请说明理由.
22.(14分)设函数f(x)=3x2+1,g(x)=2x,现有数列{an}满足条件:对于n∈N+, an>0且f(an+1)-f(an)=g(an+1+![]() ),又设数列{bn}满足条件:bn=
),又设数列{bn}满足条件:bn=![]() (a为正数,n∈N+).
(a为正数,n∈N+).
(1)求证:数列{an}为等比数列;
(2)求证:数列![]() 是等差数列;
是等差数列;
(3)设k,L∈N+,且k+L=5,bk=![]() ,bL=
,bL=![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(4)如果k+L=M0(k,L∈N+,M0>3且M0是奇数),且bk=![]() ,bL=
,bL=![]() ,求从第几项起an>1恒成立.
,求从第几项起an>1恒成立.
答案:
(理科)试题(三)
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | D | B | B | A | B | D | A | D | C | D |
二、填空题
13.![]() 14.20 15.
14.20 15.![]() 16.12
16.12
三、解答题
17.解:(1)在△ABC中有B+C=π-A,由条件可得 4[1-cos(B+C)]-4cos2A+2=7.
又∵ cos(B+C)=-cosA, ∴4 cos2A-4cosA+1=0
解得:cosA=![]() , 又A∈(0,π),∴ A=
, 又A∈(0,π),∴ A=![]() .
.
(2)由cosA=![]() 知
知 ![]() =
=![]() , 即
, 即![]() .
.
又a=![]() ,b+c=3,代入得
,b+c=3,代入得 ![]() .
.
由![]()
![]()
![]() 或
或 ![]()
18.解:(1)由AB平行且等于CD,CD平行且等于EF,有AB平行且等于EF,从而四边形ABFE是平行四边形
∵ 平面AC⊥平面DF,AD⊥CD,∴AD⊥平面DF,AD⊥EF
又EF⊥DE,∴EF⊥平面ADE ∴EF⊥AE
∴平行四边形ABFE是矩形且不是正方形
(2)如图,建立空间直角坐标系,则C(0,0,0),D(a,0,0),
|
则![]() =(a,0,-a),
=(a,0,-a),![]() =(
=(![]() ,
,![]() ,
,![]() )
)
∵![]() ·
·![]() =
=![]() +0-
+0-![]() =0
=0
∴![]() ⊥
⊥![]() ,即BD与CP所成的角是90°
,即BD与CP所成的角是90°
(3)由P(![]() ,
,![]() ,
,![]() ),N(
),N(![]() ,
,![]() ,0),
,0),
M(![]() ,0,
,0,![]() ),
),
得 ![]() =(0,-
=(0,-![]() ,0),
,0),![]() =(0,0,-
=(0,0,-![]() )
)
∵![]() ·
·![]() =0, ∴
=0, ∴![]() ⊥
⊥![]()
又![]() =
=![]() ,所以△MNP是等腰直角三角形.
,所以△MNP是等腰直角三角形.
另解提示:用非向量的方法解(2)与(3)时,可行先连结BE与DF,再进行推理与运算.
19.解:(1)设P上、P下、P左、P右分别表示点A向上、下、左、右移动的概率,点A经过2秒到达点C,只能是一秒向上移动,一秒向右移动.所以点A经过2秒到达C的路线对应“上、右”或“右、上”两种情况.
故所求概率为P=2P上·P右=2×![]() ×
×![]() =
=![]()
(2)仿(1)可知,经过3秒点A到达点D的路线对应于“上、上、右”的一个排列,所以经过3秒后点A到达点D的概率为:
PA→D=3P右·P上·P上=3×![]() ×
×![]() ×
×![]() =
=![]()
经过3秒点B到达点D的路线对应于“左、上、下”或“左、左、右”的一个排列,所以经过3秒后点B到达点D的概率为
PB→D=A![]() ×
×![]() ×
×![]() ×
×![]() +3×
+3×![]() ×
×![]() ×
×![]() =
=![]()
又∵上述两事件为独立事件,∴所求概率为:P=![]() ×
×![]() =
=![]()
20.(1)解:由题意知c=0,又f(x)为奇函数,即f(x)+ f(-x)=0,得a=0,则f′(x)=3x2-b.
若f(x)在[1,+∞)上是增函数,则f′(x)≥0恒成立,即b≤(3x2)min=3.
若f(x)在[1,+∞)上是减函数,则f′(x)≤0恒成立,这样的b不存在.
综上可得,a=c=0,b≤3.
(2)证法一:设f(x0)=m,由f(f(x0))= x0得f(m)= x0,
于是有 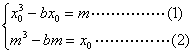
(1)-(2)得(![]() -
-![]() )-b(
)-b(![]() -m)=m-
-m)=m-![]() ,
,
化简可得(![]() -m)(
-m)(![]() +m
+m![]() +
+![]() +1-b)=0
+1-b)=0
∵![]() ≥1,f(x0)=m≥1,∴
≥1,f(x0)=m≥1,∴![]() +m
+m![]() +
+![]() +1-b≥4-b≥1>0
+1-b≥4-b≥1>0
故![]() -m=0,即有f(x0)=
-m=0,即有f(x0)=![]()
证法二:假设f(x0)≠![]() ,设f(x0)=a.
,设f(x0)=a.
①如果![]() ,由(1)知f(x)在[1,+∞)上是单调递增,
,由(1)知f(x)在[1,+∞)上是单调递增,
∴f(f(x0))=f(a)>f(x0)>x0
这与已知f(f(x0))= x0矛盾.
②如果![]() ,仿①同理可推出矛盾.
,仿①同理可推出矛盾.
由①与②可知,假设不成立.所以有f(x0)= x0.
21.解:(1)由题意可得点M(x,y)到两定点F1(0,![]() )、F2(0,-
)、F2(0,-![]() )的距离和为4,故轨迹C是以F1、F2为焦点的椭圆,其方程为 x2+
)的距离和为4,故轨迹C是以F1、F2为焦点的椭圆,其方程为 x2+![]() =1.
=1.
(2)显然x=-2与曲线C无交点,故直线L的斜率存在,设直线L的方程为y=k(x+2),并设点A、B的坐标分别为A(x1,y1)、B(x2,y2).
由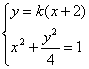 得(4+k2)x2+4 k2x+4 (k2-1)=0
得(4+k2)x2+4 k2x+4 (k2-1)=0
△=16k4-16(4+ k2)(k2-1)=-16(3 k2-4)>0![]() k2<
k2<![]()
∴x1+x2=-![]() ①
x1x2=
①
x1x2=![]() ②
②
∵![]() =
=![]() +
+![]() ∴四边形OAPB为平行四边形
∴四边形OAPB为平行四边形
若存在直线L使得四边形OAPB为矩形,则![]() ·
·![]() =0
=0
∴x1x2+ y1y2=(1+ k2)x1x2+2k2(x1+x2)+4k2=0 ③
将①②代入③解得k2=![]()
设P(x0,y0),则x0=
x1+x2=-![]() ,故点P不在直线x=-
,故点P不在直线x=-![]() 上
上
即不存在这样的直线L使得四边形OAPB为矩形.
另解提示:解答第(2)题时,如果先利用OP中点即为AB的中点,可以求得k2=![]() .与上面的解法一样还可求得k2=
.与上面的解法一样还可求得k2=![]() ,这是不可能的,所以不存在这样的直线L使得四边形OAPB为矩形.
,这是不可能的,所以不存在这样的直线L使得四边形OAPB为矩形.
22.解:(1)∵f(x)=3x2+1,g(x)=2x,f(an+1)-f(an)=g(an+1+![]() )
)
∴3(an+1)2+1-3a2n-1=2(an+1+![]() ),即6an=2an+1
),即6an=2an+1
∴![]() =3 ∴数列{an}是以3为公比的等比等列.
=3 ∴数列{an}是以3为公比的等比等列.
(2)∵bn=![]() ∴
∴![]() =
=![]() ,
,![]() =
=![]()
∴![]() -
-![]() =
=![]() =
=![]()
∴数列{![]() }是以
}是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列
的等差数列
(3)为方便起见,记数列{![]() }的公差为
}的公差为![]() ,由于
,由于![]() .
.
∴ ![]() , ∴
, ∴![]()
∴![]()
∴![]() =
=![]()
(4)若l+k=M0,由(3)可知 ![]() ==
==![]() =3 M0-3n+1
=3 M0-3n+1
假设第M项后面的项满足an>1恒成立,
由于![]() ,∴0<a<1,所以只要
,∴0<a<1,所以只要![]() <0,即
<0,即
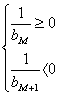
![]()
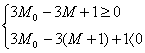
![]()
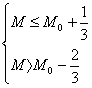
又M∈N+
∴M=M0,即数列{an}从第M0+1项起以后的项满足an>1.

