湖南省示范性中学2006届高三联考试卷
文科数学(一)
命题人:长沙市长郡中学高级教师 姜海平
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共21小题,满分150分,时量120分钟
参考公式:
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]() 如果事件
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() 如果事件
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么在
,那么在![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率 ![]()
第Ⅰ卷(选择题 共50分)
一、选择题:本大题 共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1、已知集合M=![]() ,N=
,N=![]() ,且全集I=R,则(CIM)
,且全集I=R,则(CIM)![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、在一次歌手大赛上,七位评委为某位歌手打出的分数如下:
9.4 8.4 9.4 9.9 9.6 9.4 9.7
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )
A. 9.4, 0.484 B. 9.4, 0.016
C. 0.95, 0.04 D. 9.5, 0.016
3、 从8名女生,4名男生中选出6名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法种数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、曲线![]() 在
在![]() 处的切线的倾斜角为
( )
处的切线的倾斜角为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、在等差数列![]() 中,
中,![]() 则
则![]() ( )
( )
A.24 B.22 C.20 D.-8
6、某家庭电话,打进的电话响第一声时被接的概率为![]() ,响第二声时被接的概率为
,响第二声时被接的概率为![]() ,响第三声时被接的概率为
,响第三声时被接的概率为![]() ,响第四声时被接的概率为
,响第四声时被接的概率为![]() ,则电话在响前四声内被接的概率为
( )
,则电话在响前四声内被接的概率为
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.![]()
7、若不等式![]() 成立的充分非必要条件是
成立的充分非必要条件是![]() ,则实数a的取值范围是 ( )
,则实数a的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
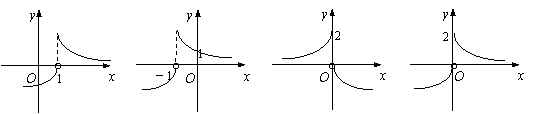 8、已知函数
8、已知函数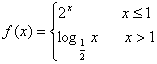 ,则f (1-x)的图象是
( )
,则f (1-x)的图象是
( )
A B C D
9、已知函数y=f(x)是偶函数,且y=f(x-2)在[0,2]上是单调递减函数,则 ( )
A. f(-1)<f(2)<f(0) B. f(-1)<f(0)<f(2)
C. f(0)<f(-1)<f(2) D. f(2)<f(-1)<f(0)
|
10、为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为 ( )
A.0.27,78 B.0.27,83 C.2.7,78 D.2.7,83
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题 共5小题,每小题4分,共20分,把答案填在题中横线上.
11、函数y=![]() (x
(x![]() )的反函数的定义域为__________.
)的反函数的定义域为__________.
12、设A={1, 2, 3, 4, 5, 6}, B={1, 3, 5, 7, 9}, 集合C是从A![]() B中任取2个元素组成的集合,
则C
B中任取2个元素组成的集合,
则C![]() A
A![]() B的概率是__________.
B的概率是__________.
13、在等比数列![]() 中,
中,![]() ,
,![]() 则
则![]() 的值为__________.
的值为__________.
14、已知函数![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是________.
的取值范围是________.
15、对任意两实数![]() 定义运算“
定义运算“![]() ”如下:
”如下: 函数
函数![]()
![]() 的值域为__________.
的值域为__________.
三、解答题:本大题 共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
设函数f(x)=![]() ,不等式
,不等式![]() ,试求不等式
,试求不等式![]() 的解集.
的解集.
17. (本小题满分12分)
已知集合A=![]()
![]()
![]() ,问同时满足B
,问同时满足B![]() A,C
A,C![]() A的实数
A的实数![]() 是否存在?若存在,求出
是否存在?若存在,求出![]() 所有的值,若不存在,请说明理由.
所有的值,若不存在,请说明理由.
18.(本小题满分14分)
已知:命题p:![]() 是
是![]() =
=![]() 的反函数,且
的反函数,且![]()
命题q:集合A=![]()
求实数![]() 的取值范围,使命题p、q中有且只有一个为真命题.
的取值范围,使命题p、q中有且只有一个为真命题.
19. (本小题满分14分)
已知等差数列![]() 的前9项和为153.
的前9项和为153.
(1)数列![]() 中是否存在确定的项,若存在,请求出该项,若不存在,请说明理由;
中是否存在确定的项,若存在,请求出该项,若不存在,请说明理由;
(2)若![]() ,求数列
,求数列![]() 前n项的积
前n项的积![]() ;
;
(3)在(2)的条件下,若从数列![]() 中,依次取出第二项、第四项、第八项,…,第
中,依次取出第二项、第四项、第八项,…,第![]() 项,按原来的顺序组成一个新的数列
项,按原来的顺序组成一个新的数列![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
20、(本小题满分14分)
已知函数![]() 在
在![]() 处取得极值,
处取得极值,
(1)用![]() 表示
表示![]() ;
;
(2)设函数![]() 如果
如果![]() 在区间
在区间![]() 上存在极小值,求实数
上存在极小值,求实数![]()
的取值范围.
21.(本小题满分14分)
某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知该厂生产这种仪器的次品率P与日产量x(件)之间满足关系:
P=
已知每生产一件合格的仪器可盈利A元,但每生产一件次品将亏损![]() 元,厂方希望定出适当的日产量.
元,厂方希望定出适当的日产量.
(1)试判断:当日产量x(件)超过94件时,生产这种仪器能否盈利?说明理由;
(2)当日产量x(件)不超过94件时,试将生产这种仪器每天的盈利额T(元)表示成日产量x(件)的函数;
(3)为了获得最大利润,日产量x应为多少件?
湖南省示范性中学2006届高三联考试卷
文科数学(一) 参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | A | D | A | B | A | D | C | A |
二、填空题
11.![]() 12.
12. ![]() 13. 192
13. 192
14. ![]() 15
.
15
. ![]()
三、解答题
16.解:![]()
由题设可得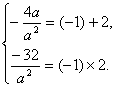 解得
解得![]() ………………………..6分
………………………..6分
![]()
![]()
由![]() ,即
,即![]() 变形得
变形得![]()
解得![]()
![]() 原不等式的解集为
原不等式的解集为 ![]() …………………………….12分
…………………………….12分
17.解:A=![]() ,
,![]() B
B![]() A,
A,![]() B有三种可能:
B有三种可能:![]()
![]()
若![]() ,则
,则![]() 无解.又当
无解.又当![]() 即
即![]() 时,B=
时,B=![]() ,
,
符合要求,![]() …………………………………………………………………….6分
…………………………………………………………………….6分
由C![]() A得
A得![]() 或
或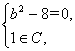 或
或 或C=A.
或C=A.
解得 ![]() …………………………………………………11分
…………………………………………………11分
综上所述,存在![]()
![]() 满足题设要求. ……………….12分
满足题设要求. ……………….12分
18.解:![]()
由![]() 得
得![]() 解得
解得![]() ………………………………….4分
………………………………….4分
设![]() 的判别式为
的判别式为![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() ,
,
![]() ……………………………………………………………………..5分
……………………………………………………………………..5分
当![]() 时,由
时,由![]() ,得
,得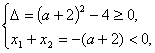 解得
解得![]() .综上,
.综上,![]() ..8分
..8分
(1)要使P真q假,则![]() 解得
解得![]()
(2)要使P假q真,则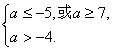 解得
解得![]() …………………………13分
…………………………13分
所以当![]() 的取值范围是
的取值范围是![]() 时,命题p、q中有且只有一个为真命题. .14分
时,命题p、q中有且只有一个为真命题. .14分
19.解:(1)数列![]() 中存在确定的项. …………………………………………1分
中存在确定的项. …………………………………………1分
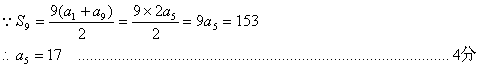
(2)设数列![]() 的公差为d,则
的公差为d,则
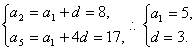
![]() . ……………………………………………………………7分
. ……………………………………………………………7分
![]()
![]() ………………9分
………………9分
(3)![]()
![]()
……………………………………………………………………………………………14分
20.解:(1)![]()
![]()
…………………………………………………………………………………………….4分
(2)由已知![]()
![]() 令
令![]() =0
=0![]()
①若![]() ,则当
,则当![]() 时,
时,![]() >0;当
>0;当![]() 时,
时,![]() .
.
所以当![]() 时,
时,![]() 在
在![]() 有极小值.
有极小值.
②同理当![]() 时,
时,![]() ,即
,即![]() 时,
时,![]() 在
在![]() 有极小值.
有极小值.
综上所述:当![]() 时,
时,![]() 在
在![]() 有极小值. ……………14分
有极小值. ……………14分
21.解:(1)当x>94时,P=![]() ,
,
![]() 每日生产的合格品为
每日生产的合格品为![]() 件,次品为
件,次品为![]() 件,
件,
![]() 合格品共可盈利
合格品共可盈利![]() A,次品共亏损
A,次品共亏损![]() .
.
![]()
![]() A-
A-![]() A=0,
A=0,
![]() 盈亏相抵,即日产量超过94件时,不能盈利…………….4分
盈亏相抵,即日产量超过94件时,不能盈利…………….4分
(2)当1![]() 时,P=
时,P=![]() ,
,
![]() 每日生产的合格品为
每日生产的合格品为![]() 件,次品为
件,次品为![]() 件,
件,
![]() T=
T=![]()
=![]() (1
(1![]() ………………8分
………………8分
(3)由(1)可知,日产量超过94件时,不能盈利,
当1![]() 时,T=
时,T=![]() =
=![]() ,
,
![]() ,
,![]()
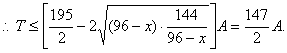
当且仅当96![]() 即x=84(件)时等号成立
即x=84(件)时等号成立
所以要获得最大利润,日产量应为84件……………………………….14分
