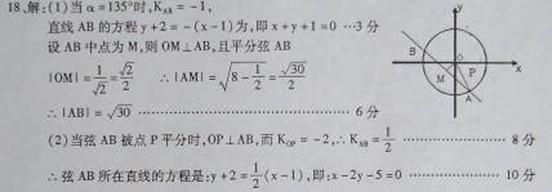高中数学必修2模块测试试卷C卷
一、选择题(每小题4分,共40分)
1.若直线经过A (-2![]() , 9)、B(6
, 9)、B(6![]() , -15)两点, 则直线A B的倾斜角是( )
, -15)两点, 则直线A B的倾斜角是( )
A.45° B.60° C.120° D.135°
2. 已知圆x2+y2+4x-2y-4=0,则圆心、半径的长分别是( )
A. (2, -1) ,3 B. (-2, 1) ,3 C. (-2, -1) ,3 D. (2, -1) ,9
3. 设正方体的表面积为24,那么其内切球的体积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.一个平行于圆锥底面的平面将圆锥的高分成相等的两段,那么圆锥被分成的两部分的侧面积的比是( )
A.1:1 B. 1:2 C. 1:3 D. 1:4
5. 圆x2+y2-2x-8=0和圆x2+y2+2x-4y-4=0的公共弦所在的直线方程是 ( )
A.x+y+1=0 B. x+y-3=0 C. x-y+1=0 D. x-y-3=0
6. 以下哪个条件可判断平面α 与平面β平行( ).
A.α内有无穷多条直线都与β平行 B. α内的任何直线都与β平行
C.直线a∥α , 直线b∥α , 且a![]() β,b
β,b![]() β D. 直线a
β D. 直线a![]() α , 直线b
α , 直线b![]() β, 且a∥β,b∥α
β, 且a∥β,b∥α
7. 直线x-2y+1=0关于直线x=1对称的直线的方程是( )
A. x+2y-1=0 B. x+2y-3=0 C. 2x+y-1=0 D. 2x+y-3=0
8. 已知点P是圆(x-3)2+y2=1上的动点,则点P到直线y=x+1的距离的最小值是( )
A. 3
B. 2![]() C. 2
C. 2![]() -1 D. 2
-1 D. 2![]() +1
+1
9.设是空间的三条直线,给出以下五个命题:
①若a⊥b,b⊥c,则a⊥c;②若a、b是异面直线,b、c是异面直线,则a、c也是异面直线;
③若a和b相交,b和c相交,则a和c也相交;④若a和b共面,b和c共面,则a和c也共面; ⑤若a∥b, b∥c,则a∥c;
其中正确的命题的个数是( ).
A.0 B.1 C.2 D.3
10.在侧棱长为3![]() 的正三棱锥P-ABC中,∠APB=∠BPC=∠CPA=40°过点A作截面AEF与PB、PC侧棱分别交于E、F两点,则截面的周长最小值为( )
的正三棱锥P-ABC中,∠APB=∠BPC=∠CPA=40°过点A作截面AEF与PB、PC侧棱分别交于E、F两点,则截面的周长最小值为( )
A.4 B.2![]() C.10 D.6
C.10 D.6
二、填空题(每小题4分,共16分)
11. M(-1, 0)关于直线x+2y-1=0对称点M’的坐标是 ;
12. 把一根长4m,直径1m的圆柱形木料锯成底面为正方形的木料,则方木料体积的最大值
是 ;
13. 已知点P(x, y)是圆(x-3)2+(y-![]() )2=6上的动点,则
)2=6上的动点,则![]() 的最大值是 ;
的最大值是 ;
14. 已知二面角α–l-β的平面角为45°,有两条异面直线a,b分别垂直于平面,则异面直线所成角的大小是 .
三、解答题(共44分)
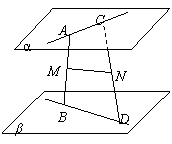 15. (8分) 设平面α∥β,两条异面直线AC和BD分别在平面α、β内,线段AB、CD中点分别为M、N,设MN=a,线段AC=BD=2a,求异面直线AC和BD所成的角.
15. (8分) 设平面α∥β,两条异面直线AC和BD分别在平面α、β内,线段AB、CD中点分别为M、N,设MN=a,线段AC=BD=2a,求异面直线AC和BD所成的角.
16. (8分)已知圆C的圆心在直线l:x-2y-1=0上,并且经过A (2, 1)、B(1, 2)两点,求圆C的标准方程.
17. (8分)已知线段AB的端点B坐标是(3, 4),端点A在圆(x+1)2+y2=4上运动,求线段AB中点M的轨迹方程.
18. (10分)已知圆x2+y2=8内有一点P(1, -2),AB为过点P且倾斜角α为的弦,
(1)当α=135°时,求弦AB的长.
(2)当弦AB被点P平分时,求出弦AB所在直线的方程.
19. (10分)如图,A、B、C、D是空间四点,在△ABC中,AB=2,AC=BC=![]() ,等边△ADB所在的平面以AB为轴可转动.
,等边△ADB所在的平面以AB为轴可转动.
(1)当平面ADB⊥平面ABC时,求CD的长;
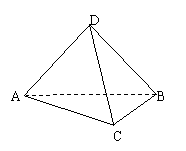 (2)当△ADB转动过程中,是否总有AB⊥CD?请证明你的结论.
(2)当△ADB转动过程中,是否总有AB⊥CD?请证明你的结论.
°
2009届六安二中高三文1、2、8班必修2模块测试试卷C卷参考答案