高中数学必修五综合练习3 文 班 考号 姓名
A卷 一.选择题(本大题共11小题,每小题5分,共55分).
1.如果![]() ,并且
,并且![]() ,那么下列不等式中不一定能成立的是( )
,那么下列不等式中不一定能成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.等比数列![]() 中,
中,![]() ,则
,则![]() =( )
=( )
A.10 B.25 C.50 D.75
3.在![]() 中,若b2
+ c2 = a2 + bc , 则
中,若b2
+ c2 = a2 + bc , 则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知数列![]() 中,
中,![]() ,
,![]() ,若
,若![]() ,则
,则![]() =( )
=( )
A.667 B.668 C.669 D.670
5.等差数列![]() 的前n项和为Sn ,若
的前n项和为Sn ,若![]() 则
则![]() ( )
( )
A.130 B.170 C.210 D.260
6.在⊿ABC中,A=45°,B=60°,a=2,则b等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
7.若将20,50,100都分别加上同一个常数,所得三个数依原顺序成等比数列,则此等比数列的公比是( ) A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
8.关于![]() 的不等式
的不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在一幢10米高的楼顶测得对面一塔吊顶的仰角为![]() ,塔基的俯角为
,塔基的俯角为![]() ,那么这座塔吊的高是(
) A.
,那么这座塔吊的高是(
) A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知![]() 且
且![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.2 B.8 C. 4 D. 1
11已知约束条件 ,目标函数z=3x+y,某学生求得x=
,目标函数z=3x+y,某学生求得x=![]() , y=
, y=![]() 时,zmax=
时,zmax=![]() , 这显然不合要求,正确答案应为( )
, 这显然不合要求,正确答案应为( )
A. x=3, y=3 , zmax=12 B. x=3, y=2 , zmax=11.C. x=2, y= 3 , zmax= 9. D. x=4, y= 0 , zmax= 12.
二、填空题(共2小题,每小题5分,共10分)
12.在⊿ABC中,![]() ,则角A =
,则角A =
13.某校要建造一个容积为8![]() ,深为2
,深为2![]() 的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为
元。
的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为
元。
三、解答题(本大题共3小题,共35分,解答应写出文字说明、证明过程或演算步骤)
14.(本题11分)已知数列![]() 的前
的前![]() 项和为
项和为![]() (1)求数列
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
15.(本题12分)在△ABC中,![]() ,cosC是方程
,cosC是方程![]() 的一个根,求
的一个根,求
①角C的度数②△ABC周长的最小值。
16.(本题12分)某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

B卷一.填空题(本大题共3小题,每小题4分,共12分)
17.已知数列{![]() }的前n项和为Sn ,若a1
= -2 ,a2=2, 且an + 2-an=1+(-1)n 则S50 =
}的前n项和为Sn ,若a1
= -2 ,a2=2, 且an + 2-an=1+(-1)n 则S50 =
18.已知三角形两边长分别为2和2![]() ,第三边上的中线长为2,则三角形的外接圆半径为
,第三边上的中线长为2,则三角形的外接圆半径为
19.不等式![]() 表示的平面区域包含点
表示的平面区域包含点![]() 和点
和点![]() 则
则![]() 的取值范围是
的取值范围是
二.解答题(本大题共3小题,共38分,解答应写出文字说明.证明过程或演算步骤)
20.(
12分)在△ABC中,sinA+cosA=![]() ,AC=2,AB=3,求① tanA的值 ; ② △ABC的面积..
,AC=2,AB=3,求① tanA的值 ; ② △ABC的面积..
21. (本小题满分12分)
过点P(1,4)作直线L,直线L与x,y的正半轴分别交于A,B两点,O为原点,
① △ABO的面积为S,求S的最小值并求此时直线l的方程;
② ②当OA+OB最小时,求此时直线L的方程
22. (本小题满分14分) 已知数列![]() 的前n项和Sn=9-6n.
的前n项和Sn=9-6n.
(1)求数列![]() 的通项公式.(2)设
的通项公式.(2)设![]() ,求数列
,求数列![]() 的前n项和.
的前n项和.
2009届六安二中高三文1、2、8必修五综合练习3答案 2008-5-30
一、选择题(本大题共11小题,每小题5分,共55分).
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 | D | B | C | D | C | A | D | B | B | C | B |
二、填空题(本大题共2小题,每小题5分,共10分)
12.![]() ; 13.3520;
; 13.3520;
三、解答题(本大题共3小题,共35分,解答应写出文字说明、证明过程或演算步骤)
14.解:(1)当![]() 时,
时,![]() ………………………1分
………………………1分
当![]() 时,
时,![]() 也适合
也适合![]() 时,
时,
∴![]() …………………………5分
…………………………5分
(2)![]() ,………………………6分
,………………………6分
∴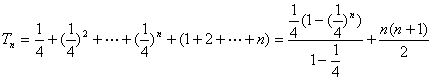 ……9分
……9分
![]() ……11分
……11分
15.解:①![]()
![]() ……2分
……2分
又![]() 是方程
是方程![]() 的一个根
的一个根 ![]() ,在△ABC中∴C =
120度…6分
,在△ABC中∴C =
120度…6分
② 由余弦定理可得:![]()
即:![]() ……8分
……8分
当![]() 时,c最小且
时,c最小且![]() 此时
此时![]() ……10分
……10分

![]() △ABC周长的最小值为
△ABC周长的最小值为![]() ……12分
……12分
16.解:设需要甲种原料x张,乙种原料y张,
则可做文字标牌(x+2y)个,绘画标牌(2x+y)个.
由题意可得:
 …………5分
…………5分
所用原料的总面积为z=3x+2y,作出可行域如图,…………8分
在一组平行直线3x+2y=t中,经过可行域内的点且到原点距离最近的直线
过直线2x+y=5和直线x+2y=4的交点(2,1),∴最优解为:x=2,y=1………10分
∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小. ………12分
B卷
一、填空题(本大题共3小题,每小题4分,共12分)
17.600. 18. 2 . 19.理:![]() .文:(-2 ,3 )
.文:(-2 ,3 )
二、解答题(本大题共3小题,共38分,解答应写出文字说明、证明过程或演算步骤)
20(本小题满分12分)
解:①∵sinA+cosA=![]() cos(A-45°)=
cos(A-45°)=![]() , ∴cos(A-45°)=
, ∴cos(A-45°)= ![]() .………2分
.………2分
又0°<A<180°, ∴A-45°=60°,A=105°. ……… 4分
∴tanA=tan(45°+60°)=![]() =-2-
=-2-![]() .………6分
.………6分
② sinA=sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°=![]() .……… 9分
.……… 9分
∴SABC=![]() AC·AbsinA=
AC·AbsinA=![]() ·2·3·
·2·3·![]() =
=![]() (
(![]() +
+![]() ).……… 12分
).……… 12分
(此题还有其它解法,类似给分)
21. (本小题满分12分)
解:依题意可设直线l的方程为:![]() (a>0 , b>0 )
(a>0 , b>0 )
则A(a , 0 ), B(0,b ), 直线L过点P(1,4), ∴![]() , ……………2分
, ……………2分
又a>0 , b>0
∴![]()
![]() ………………4分
………………4分
当且仅当![]() 取等号, S的最小值为8
取等号, S的最小值为8
此时直线方程为:![]() ,即:4x + y - 8=0…………………6分
,即:4x + y - 8=0…………………6分
②OA+OB= a + b = (a + b )(![]() )=5 +
)=5 + ![]() ……8分
……8分
当且仅当![]() 取等号, ……10分
取等号, ……10分
OA+OB的值最小, 此时直线方程为:![]() 即:2x + y - 6=0……12分
即:2x + y - 6=0……12分
法二:①依题意可设直线l的方程为:y-4 = k ( x -1 ) ( k<0 )
令 x = 0 , 则y
= 4 – k ,B( 0 , 4-k) ;令 y = 0 , 则x =![]() +1 ,A (
+1 ,A (![]() +1, 0)…2分
+1, 0)…2分
S =![]() (4-k)(
(4-k)( ![]() +1)=
+1)= ![]() (
(![]() - k + 8 )≥8 ,…………4分
- k + 8 )≥8 ,…………4分
当且仅当-16/k = -k时,即 k = -4时取等号, S的最小值为8 ,
此时直线方程为:y-4 = -4( x -1 ),即:4x + y - 8=0…………6分
②OA+OB=( ![]() +1) + (4-k) =
+1) + (4-k) = ![]() -k + 5 ≥4 + 5 =9 ,……8分
-k + 5 ≥4 + 5 =9 ,……8分
当且仅当![]() = -k时,即 k = -2时取等号, OA+OB的值最小, ……………10分
= -k时,即 k = -2时取等号, OA+OB的值最小, ……………10分
此时直线方程为::y-4 = -2 ( x -1 ) 即:2x + y - 6=0……………12分
22. (本小题满分14分)解:(1)![]() 时,
时,![]() ∴
∴![]() ………理1分,文2分
………理1分,文2分
![]() 时,
时,![]() ∴
∴![]() ………理3分,文5分
………理3分,文5分
∴通项公式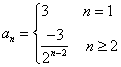 ………理5分,文7分
………理5分,文7分
(2)当![]() 时,
时,![]() ∴
∴![]() ………理6分,文9分
………理6分,文9分
![]() 时,
时,![]() ∴
∴![]() ………理7分,文11分
………理7分,文11分
∴![]()
![]() ………理9分,文14分
………理9分,文14分
(3)∵![]()
![]() ,………理10分
,………理10分
![]() 两边同时乘以2n,得
两边同时乘以2n,得![]() 即
即![]() ∴数列{
∴数列{![]() +4}是以6为首项,4为公比的等比数列,
+4}是以6为首项,4为公比的等比数列,![]() +4 = 6×4n-1,∴
+4 = 6×4n-1,∴![]() (n≥2) ………理13分
(n≥2) ………理13分
又C1=1, 满足上式
∴通项公式![]() ………理14分
………理14分
法二:(迭代法) ![]() =
= ![]() = …… =
= …… =![]()
=![]()
![]() 又C1=1, 满足上式
又C1=1, 满足上式
∴通项公式![]()