高中数学必修一和必修二综合测试A
考号 班级 姓名
一、选择题（每小题5分，共10小题，共50分）
1、设集合
，
，且
，则：（ ）
A．
B．
C．
D．
2、对于一个底边在
轴上的三角形，采用斜二测画法作出其直观图，其直观图的面积是原三角形面积的：（ ）
A. 2倍
B. 
倍 C. 
倍 D. 
倍
3. 已知函数
，则
的值是（ ）
A. 8 B. 
C.
9
D. 
4. 设
则下列关系正确的是：（ ）
A. 
B. 
C. 
D. 
5. 函数
的零点所在区间为：（ ）
A． （
1，0） B. （0，1） C. （1，2） D. （2，3）
6. 函数
的定义域为
，且对其内任意实数
均有：
，则在上是：（ ）
A. 增函数 B. 减函数 C. 奇函数 D. 偶函数x
7. 在x轴上的截距为2且倾斜角为135°的直线方程为：（ ）
Ａ. ｙ＝－ｘ＋２ Ｂ. ｙ＝－ｘ－２ Ｃ. ｙ＝ｘ＋２ Ｄ. ｙ＝ｘ－２
8. 设点M是Z轴上一点，且点M到A（1，0，2）与点B（1，－3，1）的距离相等，则点M的坐标是：（ ）
A．（－3，－3，0） B．（0，0，－3）
C．（0，－3，－3） D．（0，0，3）
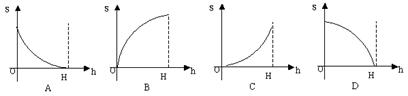
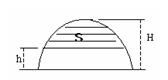9. 如图所示，阴影部分的面积
是
的函数. 则该函数的图象是：（ ）
10. 将直线
向左平移3个单位，再向上平移2个单位得到直线
，则直线
之间的距离为：（ ）
A．
B．
C．
D．
二、填空题（每小题6分，共5个小题，共30分）
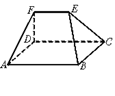
11、如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，EF=
，EF与面AC的距离为2，则该多面体的体积是_______
12、若定义在区间（1，2）内的函数
满足
，则
的取值范围是
；
13、已知镭经过100年，质量便比原来减少4.24％，设质量为1的镭经过年后的剩留量为
，则
的函数解析式为 .
14、已知l⊥α，m
β，则下面四个命题：
①α∥β则l⊥m ②α⊥β则l∥m ③l∥m则α⊥β ④l⊥m则α∥β
其中正确的是___ _____
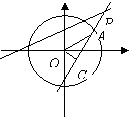
15、在圆 
上，与直线4x+3y－12=0的距离最小的点的坐标
.
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
三、解答题
16（14分）．(1)、求经过直线
和
的交点，且垂直于直线
的直线方程.(2)、直线l经过点
，且和圆C：
相交，截得弦长为
，求l的方程.
17（14分）．某飞机制造公司一年中最多可生产某种型号的飞机100架。已知制造x架该种飞机的产值函数为R(x)=3000x-20x2 (单位：万元），成本函数C（x)=500x+4000 (单位：万元）。利润是收入与成本之差，又在经济学中，函数¦（x)的边际利润函数M¦x)定义为：M¦x)=¦(x+1)-¦(x).
①、求利润函数P(x)及边际利润函数MP(x)；（利润=产值-成本）
②、问该公司的利润函数P(x)与边际利润函数MP(x)是否具有相等的最大值？
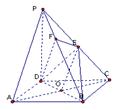
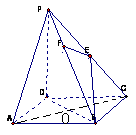18（21分）．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
（1）证明 PA//平面EDB；
（2）证明PB⊥平面EFD；
（3）求二面角C-PB-D的大小．
19（21分）．若非零函数
对任意实数
均有¦(a+b)=¦(a)·¦(b)，且当
时，
.
（1）求证：
；
（2）求证：为减函数；
（3）当
时，解不等式
参考答案
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | D | C | C | B | A | B | A | B |
★11． ★12题 :0<a<； ★13题: 
;
★14题：①③；
★15题: 
17．(1)、解：由方程组
，解得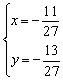
，所以交点坐标为
.
又因为直线斜率为
， 所以求得直线方程为27x+54y+37=0.
（2）、．解：如图易知直线l的斜率k存在，设直线l的方程为
.
圆C：的圆心为（0，0）, 半径r=5，圆心到直线l的距离
.
在
中，
，
.
，
∴ 
或
.
l的方程为
或
.
19．解：①P(x)= R(x)- C（x)= -20x2+2500x-4000 (x∈N*,且x∈[1,100])；
MP(x)=
P(x+1)- P(x)=-40x+2480(x∈N*,且x∈[1,100])； ②P(x)= -20（x-）2+74125 (x∈N*,且x∈[1,100])；则当x=62或63时，P（x)max=74120（元），因为MP(x) =-40x+2480为↘，则当x=1时，MP(x)max =2440元，故利润函数与边际利润函数不具有相等的最大值。
20．解：（1）证明：连结AC，AC交BD于O．连结EO．∵ 底面ABCD是正方形，∴ 点O是AC的中点．在△PAC中，EO是中位线，∴ PA//EO．而
平面EDB，且
平面EDB，所以，PA//平面EDB．
（2）证明：∵ PD⊥底面ABCD，且
底面ABCD， ∴ PD⊥DC.
∵ 底面ABCD是正方形，有DC⊥BC, ∴ BC⊥平面PDC． 而
平面PDC，∴ BC⊥DE.又∵PD=DC，E是PC的中点，∴ DE⊥PC. ∴ DE⊥平面PBC．
而
平面PBC，∴ DE⊥PB．又EF⊥PB，且
，所以PB⊥平面EFD．
（3）解：由（2）)知，PB⊥DF，故∠EFD是二面角C-PB-D的平面角，由（2）知，DE⊥EF，PD⊥DB.
设正方形ABCD的边长为a，则
在
中，
．在
中，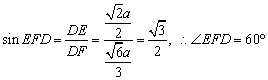
.所以，二面角C-PB-D的大小为60°.
21．解：（1）
（2）设
则
,为减函数
（3）由
原不等式转化为
，结合（2）得：
故不等式的解集为
.