数学理科 模拟试卷五
一、选择题
1. 若AB,AC,B={0,1,2},C={0,2,4},则满足上述条件的集合A的个数为( )
(A) 4 (B) 3
(C) 2 (D) 1
2. 以下命题正确的是:( )
(A) 若直线a在平面α外,则直线a与平面α内任何一点都可以确定一个平面。
(B) 若直线a平行于直线b,则a平行于过b的任何平面。
(C) 若平面α内有无数条直线平行于平面β,则α∥β。
(D) 若a、b是异面直线,则经过a且与b垂直的平面可能不存在。
3. 函数y=sin|x|(x∈R) ( )
(A) 是偶函数,又是周期函数
(B) 是偶函数,不是周期函数
(C) 是奇函数,不是周期函数
(D) 不是奇函数,是周期函数
x=sinθ
4. 方程 (θ为参数)所表示的曲线上的一个点的坐标是( )
y=cos2θ
(A) (2, -7) (B) (1. 1)
(C) (![]() ,
,![]() )
(D) (
)
(D) (![]() ,-
,-![]() )
)
5. 等比数列 {a![]() } 中,a
} 中,a![]() =7,前三项之和 S
=7,前三项之和 S![]() =21,则公比q的值是( )
=21,则公比q的值是( )
(A) 1
(B) -![]()
(C) 1或 -![]() (D) -1或
(D) -1或![]()
6. 平移坐标轴,使原坐标系中点(1,2)在新坐标系中的坐标为(2,0),若曲线C 在原坐
标系中的方程为f(x,y)=0,则曲线C在新坐标系x' o' y'中的方程为( )
(A) f(x'-1, y'+2)=0 (B) f(x'-1, y'-2)=0
(C) f(x'+1, y'+2)=0 (D) f(x'+1, y'-2)=0
7. 记函数 y=arccosx(|x|≤1)的图象为c1, y=arcsinx(|x|≤1)的图象为c2,
要得到c,只要:( )
(A) 把c![]() 向上平移
向上平移![]() 个单位
个单位
(B) 作出 c![]() 关于y轴对称的图形
关于y轴对称的图形
(C) 把C![]() 向上平移
向上平移![]() 个单位得c
个单位得c![]() 再作C
再作C![]() 关于y轴对称的图形。
关于y轴对称的图形。
(D) 把c![]() 向下平移
向下平移![]() 个单位得c
个单位得c![]() ,再作出c
,再作出c![]() 关于y轴对称的图形。
关于y轴对称的图形。
8. 关于x的方程a![]() =-x
=-x![]() +2x+a (a>0, 且a≠1) 的解的个数是( )
+2x+a (a>0, 且a≠1) 的解的个数是( )
(A) 0 (B) 1
(C) 2 (D) 不确定应视a的值而定
9. 若平面α⊥平面β,α∩β=a,P∈α,P∈直线b,则b⊥α是b⊥β的:( )
(A) 充分非必要条件
(B) 必要非充分条件
(C) 充要条件
(D) 既非充分又非必要条件
10. 非零复数Z满足![]() <argZ<
<argZ<![]() ,ω=
,ω=![]() ,则argω的取值范围是:( )
,则argω的取值范围是:( )
(A) (0, ![]() )
(B) (
)
(B) (![]() , π)
, π)
(C) (π, ![]() )
(D) (
)
(D) (![]() , 2π)
, 2π)
11. 等差数列{a![]() }共有2n+1项,其中奇数项之和为319,偶数项之和为290,
}共有2n+1项,其中奇数项之和为319,偶数项之和为290,
则第n+1项为:( )
(A) 28 (B) 29
(C) 30 (D) 31
12. 5个不同的建筑工程,由4个工程队分别承包,每个工程队至少承包一个,且5个工
程全部承包完,则不同的承包方案有:( )
(A) 240种 (B) 480种
(C) 120种 (D) 360种
|
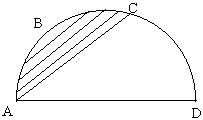
13. 如图,半圆直径AD=2r,B,C两点将半圆弧三等分,以AD为轴将弓形ABC旋形一周, 则所得旋转体的表面积为:( ) |
(A) ![]() πr
πr![]() (B) 3πr
(B) 3πr![]()
(C) ![]() πr
πr![]() (D)
(D) ![]() πr
πr![]()
14. 已知椭圆 ![]() 的一条准线方程是ρcosθ=-2,那么,另一条准线的极坐
的一条准线方程是ρcosθ=-2,那么,另一条准线的极坐
标方程是:( )
(A) ρcosθ=2 (B) ρcosθ=4
(C) ρcosθ=![]() (D)
ρcosθ=
(D)
ρcosθ=![]()
15. 已知 ![]() (x≥0), a=f
(x≥0), a=f![]() (log
(log![]() 2), b=f
2), b=f![]() (cos2),c=f
(cos2),c=f![]() [arcsin(-
[arcsin(-![]() )],
)],
则a, b, c的大小关系为:( )
(A) a>b>c (B) a>c>b
(C) b>c>a (D) c>b>a
二、填空题
16. 方程sin2x ctgx=0的解集是:( )
(A) {x|x=kπ+![]() ,k∈z}
,k∈z}
(B) {x|x=kπ-![]() ,k∈z}
,k∈z}
(C) {x|x=2kπ+![]() ,k∈z}
,k∈z}
(D) {x|x=2kπ-![]() ,k∈z}
,k∈z}
17. 等边圆锥(轴截面为正三角形)的轴截面面积为4![]() cm
cm![]() ,则该圆锥的体积=( )
,则该圆锥的体积=( )
(A) ![]() (B)
(B)
![]()
(C)![]() (D)
(D) ![]()
18. 二项式 ![]() 的展开式中 x
的展开式中 x![]() 的系数为:( ) (用数字作答)
的系数为:( ) (用数字作答)
(A) ![]() (B) +
(B) +![]()
(C) -![]() (D) -
(D) -![]()
19. 经过抛物线y![]() =-4x的焦点且与直线y=2x所成的角为45°的直线方程为:( )
=-4x的焦点且与直线y=2x所成的角为45°的直线方程为:( )
(A) y=-3x-3或 y=![]() x-
x-![]()
(B) y=-3x-3或 y=![]() x+
x+![]()
(C) y=-3x-3或 y=-![]() x-
x-![]()
(D) y=+3x+3或 y=![]() x+
x+![]()
20. 数列 {a![]() } 的通项公式为
} 的通项公式为 ![]() 前n项和为 S
前n项和为 S![]() ,若
,若 ![]()
(a为实常数),则a的值= ( )
21. 某工厂生产机器的产量,第二年比第一年增长的百分率为 P![]() ,第三年比第二年增长的百分率为 P
,第三年比第二年增长的百分率为 P![]() ,第四年比第三年增长的百分率为 P
,第四年比第三年增长的百分率为 P![]() ,设年平均增长率为P,且
,设年平均增长率为P,且 ![]() 为定值,则P的最大值为:( )
为定值,则P的最大值为:( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)![]()
三、解答题
22. 已知 sinα+cosα=-![]() , (
, (![]() <α<2π).
<α<2π).
求 ![]() 的值为:( )
的值为:( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
[解析]
23. 已知虚数Z同时满足以下两个条件:i) |![]() -3|=|
-3|=|![]() -3i|,
-3i|,
ii) Z-1+![]() 是实数,求Z ( )
是实数,求Z ( )
(A)![]()
(B)![]()
(C)![]()
(D)![]()
[解析]
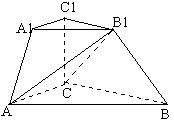
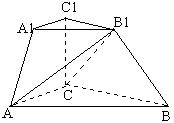
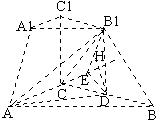
| 24. 如图,三棱台 ABC-A
AC=a, BC=2a C (Ⅰ) 求二面角 B |
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
| [解析] |
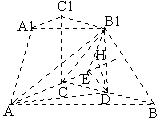
(Ⅱ) 求点B到平面B![]() AC的距离:( )
AC的距离:( )
|
(A) (C) |
[解析]
25. 解不等式 ![]() >
>![]() ,其中a∈(100,
,其中a∈(100,![]() ) ( )
) ( )
(A)0<x<1或![]() <x<lga+
<x<lga+![]()
(B)0<x<1或![]() <x<lga+
<x<lga+![]()
(C)0<x<1或![]() <x<lga+
<x<lga+![]()
(D) 0<x<1或![]() <x<lga+
<x<lga+![]()
[解析]
26. 已知曲线M:x![]() -y
-y![]() =m (x>0,m为正常数),直线L与曲线M的实轴不垂直,
=m (x>0,m为正常数),直线L与曲线M的实轴不垂直,
且依次交直线y=x,曲线M,直线y=-x,于A、B、C、D四个点。O为原点。
Ⅰ) 若|AB|=|BC|=|CD|,求证:△AOD的面积为定值。
[解析]
Ⅱ) 若△BOC的面积等于△AOD面积的 ![]() , 求证:|AB|=|BC|=|CD|.
, 求证:|AB|=|BC|=|CD|.
[解析]
参 考 答 案
一、
1. A 2. D 3. B 4. C 5. C
6. A 7. C 8. C 9. B 10. D
11. B 12. A 13. A 14. D 15. B
二、
16. A 17. D 18. C 19. B 20. ( 3 ) 21. C
三、解答题
22. C
[解析] 原式
![]()
![]()
![]()
∵ sinα+cosα=![]() ,∴ 1+2sinαcosα=
,∴ 1+2sinαcosα= ![]() ,
,
∴ sin2α=![]()
∵ sinα+cosα<0且![]() <α<2π
<α<2π
∴![]() <α<
<α<![]() ,3π<2α<
,3π<2α<![]() π
π
∴ cos2α=![]()
∴ 原式=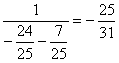
23. B
[解析] 设Z=x+yi (x,y∈R,且y≠0), 则![]() =x-yi
=x-yi
∵ |![]() -3|=|
-3|=|![]() -3i|,∴ |(x-3)-yi|=|x-(y+3)i|
-3i|,∴ |(x-3)-yi|=|x-(y+3)i|
(x-3)![]() +y
+y![]() =x
=x![]() +(y+3)
+(y+3) ![]()
∴ y=-x(y≠0)…………①
∵ y≠0, ∴ (x-1)![]() +y
+y![]() =9…………②
=9…………②
∴ ![]()
| 24.(Ⅰ)D
[解析] 作 B 是异面直线AB 二面角 B |
(Ⅱ)A
[解析] 设B到平面B![]() AC的距离为h,则
AC的距离为h,则![]()
|
∴ ∴ |
25. D
[解析] 解法:原不等式
0<x<1 1<x<2lga
(Ⅰ) 或 (Ⅱ)
![]() <1
<1
![]() >1
>1
∴ (Ⅰ) 的解为0<x<1
∴ (Ⅱ) 的解为 ![]() <x<
<x<![]()
综上所述,原不等式的角为
0<x<1或 ![]() <x<
<x<![]()
(a∈100,![]() )
)
26.
Ⅰ) [解析] 设l:y=kx+b代入x![]() -y
-y![]() =m 得(1-k
=m 得(1-k![]() )x
)x![]() -2bkx-b
-2bkx-b![]() -m=0 ①
-m=0 ①
显然,k≠±1, △=4b![]() k
k![]() +4(1-k
+4(1-k![]() )(b
)(b![]() +m)>0 b
+m)>0 b![]() +m(1-k
+m(1-k![]() )>0,
)>0,
设 B(x![]() ,y
,y![]() ),C(x
),C(x![]() ,y
,y![]() ) 则 x
) 则 x![]() x
x![]() 是①的两根
是①的两根![]() ,
,
![]() 设 A(x
设 A(x![]() ,y
,y![]() ),D(x
),D(x![]() ,y
,y![]() )
)
y=kx+b y=kx+b
由 得![]() 由
得
由
得 ![]()
y=x y=-x
∵ |AB|=|BC|=|CD| ∴ |BC|=![]() |AD|
|AD|
∴ ![]() |x
|x![]() -x
-x![]() |
| ![]() |x
|x![]() -x
-x![]() |
|
∴|x![]() -x
-x![]() |=
|=![]() |x
|x![]() -x
-x![]() |
|
![]() 整理,
整理,
得 ![]() ∵ b
∵ b![]() >0, m>0, ∴ k
>0, m>0, ∴ k![]() >1
>1
又|OA|=![]() |
|![]() |,|OD|
|,|OD|![]() |
|![]() |,∠AOD=90°,
|,∠AOD=90°,
∴ ![]() ·|OA|·|OD|
·|OA|·|OD| ![]() (定值)……
(定值)……
Ⅱ) [解析] 设BC的中点为P,AD的中点为Q,则 ![]() ,
,
![]() ∴ x
∴ x![]() =x
=x![]() ,又P、Q都在直线l上,
,又P、Q都在直线l上,
∴ P、Q重合,∴ |AP|=|DP| ∴ |AP|-|BP|=|DP|-|CP|
∴|AB|=|CD| ∵![]() ,
,
∴ |BC|=![]() |AD| ∴ |AB|+|CD|=
|AD| ∴ |AB|+|CD|=![]() |AD|
|AD|
∴ |AB|=|CD|=![]() |AD| ∴ |AB|=|BC|=|CD|
|AD| ∴ |AB|=|BC|=|CD|