数学文科:模拟试卷一
一、选择题:
每题给出的四个选项中,只有一个符合题目要求的,把所选项前的字母填在题后括号内
1. 设集合A={a,b,c},那么满足A∪B=A的集合B的个数是( )
(A) 1 (B) 7
(C) 8 (D) 10
2. 不等式![]() 的解集是( )
的解集是( )
(A) {x|o<x<1} (B) {x|x>1或x<0}
(C) {x|x>1} (D) {x|x<1}
3. 设α、β是第二象限角,且α>β,那么下面四个不等式中:
sinα>sinβ、cosα>cosβ、tgα>tgβ、ctgα>ctgβ
一定成立的不等式的个数是( )
(A) 0 (B) 1
(C) 2 (D) 3
4. 棱柱成为直棱柱的一个必要但不充分的条件是( )
(A) 棱柱有一条侧棱与底面垂直
(B) 棱柱有一条侧棱与底面的两边都垂直
(C) 棱柱有一个侧面与底面的一条边垂直
(D) 棱柱有一个侧面是矩形,且它与底面垂直
5. 圆![]() 关于直线2x+ay-b=0对称,那么点(a, b)在( )
关于直线2x+ay-b=0对称,那么点(a, b)在( )
(A) 直线3x-y-2=0上 (B) 直线3x-y+2=0上
(C) 直线3x+y-2=0上 (D) 直线3x+y+2=0上
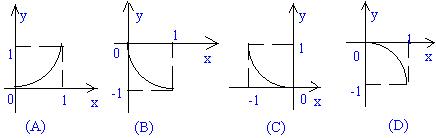 |
6. 函数
7. 某文艺队有8名歌舞演员,其中6人会演舞蹈,有5人会演歌唱节目,
现从这8人中选两个人,一人演舞蹈,另一人唱歌,则不同选法共有( )
(A) 36种 (B) 28种
(C) 27种 (D) 24种
8. 复平面上,A点对应复数1+2i,B点对应复数3-5i,向量AB绕A点逆时针旋转90°,
得向量AC,那么C点对应的复数是( )
(A) 8-2i (B) 8+2i
(C) 8+4i (D) 8-4i
9. 椭圆![]() 的焦点坐标是( )
的焦点坐标是( )
(A) (-3,2)、(1,2) (B) (-3,-2)、(1,-2)
(C) (-1,2)、(3,2) (D) (-1,-2)、(3,-2)
10. 如果![]() ,
, ![]() ,那么复数z等于( )
,那么复数z等于( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
11. 函数 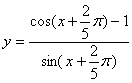 的递减区间是( )
的递减区间是( )
(A) (-∞,+∞)
(B) (![]() ),k∈z
),k∈z
(C) (![]() ),k∈z
),k∈z
(D) (![]() ),k∈Z
),k∈Z
12. 数列{a![]() }的前n项和
}的前n项和![]() ,当n是大于1 的自然数时,一定有( )
,当n是大于1 的自然数时,一定有( )
(A) nan<na1<Sn (B) Sn<nan<na1
(C) na1<Sn<n·an (D) nan<Sn<na1
13. 椭圆β![]() x
x![]() +α
+α![]() y
y![]() =α
=α![]() β
β![]() (α>β>0),双曲线
(α>β>0),双曲线![]() (p>0,q>0)有相同
(p>0,q>0)有相同
的焦点F1、F2,M是它们的一个公共点。则 |MF1|·|MF2|等于( )
(A) α-p (B)α+p
(C) α![]() -p
-p![]() (D) α
(D) α![]() +p
+p![]()
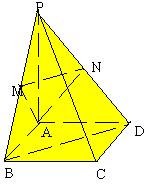
14. 四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,M、N分别是PB和PD
的中点。那么PC和过A、M、N三点的平面所成的角是( )
(A) 90° (B) 60°
(C) 45° (D) 30°
15. f(x)是定义在R上的函数,且满足f(10+x)=f(10-x)、f(20-x)=-f(20+x),
那么f(x)是( )
(A) 偶函数,也是周期函数 (B) 偶函数,但不是周期函数
(C) 奇函数,也是周期函数 (D) 奇函数,但不是周期函数
二、填空题:
16. 在![]() 的展开式中,x
的展开式中,x![]() 的系数是( )。
的系数是( )。
[解答]
17. 抛物线y![]() =4x 截直线 y=2x+m 得弦 AB,若 |AB|=
=4x 截直线 y=2x+m 得弦 AB,若 |AB|=![]() , F是抛物线的焦点,那么
, F是抛物线的焦点,那么
△FAB的面积是( )。
[解答]
18. 设二面角α-a-β的大小是60°,P是二面角内的一点,P点到α、β的距离分别为1cm、
2cm,那么点P到棱a的距离是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
[解答]
19. 不等式![]() 对一切实数x都成立,那么实数m的取值范围是( )
对一切实数x都成立,那么实数m的取值范围是( )
(A) -1<m<9 (B) 1<m<9
(C) 3<m<9 (D) -9<m<1
[解答]
三、解答题
20. 在复平面上,A、B、C三个点分别对应复数z1=1+i,z2=4+2i,z3=3+3i。
以AB为边,AC为对角线作平行四边形ABCD。
(1) 求D点对应的复数z4( )
(A) -2i (B) 1+2i
(C) 2i (D) -2i
(2) 求arg(z4)。( )
(A) ![]() (B)
(B)
![]()
(C) 1
(D)![]()
[分析解答]
21. 已知函数y=sin![]() x+2sinxcosx+3cos
x+2sinxcosx+3cos![]() x,求该函数图象的平行于y轴的对称轴方程?( )
x,求该函数图象的平行于y轴的对称轴方程?( )
(A) ![]() k∈Z
(B)
k∈Z
(B) ![]() k∈Z
k∈Z
(C) ![]() k∈Z (D)
k∈Z (D)
![]() k∈Z
k∈Z
[解答]
22. △ABC和△DBC是两个直角三角形,它们所在的平面互相垂直,AB=AC=CD=a,
P是AC边上的一点。当△PBD的面积最小时,求二面角P—BD—C的正切值?
并求此时△PBD的面积?
二面角P—BD—C的正切值是( ),
(A) ![]() (B) 1 (C)
(B) 1 (C) ![]() (D)
(D)
![]()
此时△PBD的面积是( )
(A) a![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
[解答]
23. 有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是A、B(万元),它们与投入资金x(万元)的关系有经验公式:![]() ,
, ![]() 。今有30万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为甲( )万元,乙( )万元. 能获得多大利润?( )万元
。今有30万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为甲( )万元,乙( )万元. 能获得多大利润?( )万元
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
[分析解答]:
24. 已知椭圆 ![]() (a>b>0),双曲线
(a>b>0),双曲线 ![]() ,A、B是椭圆的左、
,A、B是椭圆的左、
右顶点,P是双曲线C2右支上的一点,AP交C1于C点,PB延长后与C1交于D点,且
△ACD和△PCD面积相等。
(1) 求直线CD的倾斜角? ( )
(A) ![]() (B)
π
(B)
π
(C) ![]() (D)
(D) ![]()
[解答]:
(2) C2 的离心率e为($S*D$)值时,直线CD恰好过C1 的右焦点。
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
[解答]:
25. 数列 {an} 中,a1=a,an=a·an-1(n≥2) 数列 {bn} 中,b1=b,bn=b·an-1+c·bn-1(n≥2)
(a、b、c是常数,且b≠0,a>c>0)
(1) 求b2、b3、b4;
b2=b(a+c) ( )
b3=b(a![]() -a·c-c
-a·c-c![]() ) ( )
) ( )
b4=b(a![]() +a
+a![]() c+ac
c+ac![]() +c
+c![]() ^^3) ( )
^^3) ( )
[解答]:
(2) 猜bn 的表达式,并用数学归纳法证之;
[解答]
(3)求![]()
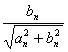
[解答]
参 考 答 案
一、
1. C
[分析解答]
B可能是ф、{a}、{b}、{c}、{a,b}、{a,c}、{b,c}、{a,b,c}。
2. A
[分析解答]
![]() < 0 <==>
< 0 <==> ![]() <
<![]() <==>
<==> ![]() >1
>1
3. A
[分析解答]
均可举出反例。
4. B
[分析解答]
注意条件是必要的,但又是不充分的,即由此不能断定棱柱为直棱柱,但直棱柱必具备
这性质。
5. C
[分析解答]
2x+ay-b=0过圆心(1,-3),故3a+b=2。
6. B
[分析解答] 函数y=f(x)的解析式可以化为 ![]()
(-1≤x≤0, 0≤y≤1) 于是y=f(x)的图象是(C)。再关于y=x对称。
7. C
[分析解答]
首先“全能”演员有3个,用不用他们?
用几个![]()
8. C
[分析解答]
![]() ,
, ![]()
∴C对应复数(7+2i)+(1+2i)=8+4i
9. D
[分析解答]
配方 (x-1)![]() +5(y+2)
+5(y+2) ![]() =5
=5
∴中心为O'(1,-2),C=2
10. B
[分析解答] 设z=x+yi(x,y∈R)
则:![]()
![]()
解之,得 ![]()
11. D
[分析解答] ![]()
![]()
12. D
[分析解答]
易知{an}是d<0的等差数列
故nan<Sn<na1
13. C
[分析解答] 设|MF1|=d1, |MF2|=d2
4c![]() =d
=d![]() +d
+d![]() -2d1·d2cosθ
-2d1·d2cosθ
对椭圆而言: 4c![]() =4a
=4a![]() -2d1d2-2d1d2cosθ
-2d1d2-2d1d2cosθ
对双曲线而言: 4c![]() =4p
=4p![]() +2d1d2-2d1d2cosθ
+2d1d2-2d1d2cosθ
由(1)、(2)解出d1d2=a![]() -p
-p![]()
14. A
|
[分析解答] 易知MN∥BD,AC⊥BD PC⊥BD ∴ PC⊥MN。 易知BC⊥平面PAB, ∴ BC⊥AM,而AM⊥PB, ∴ AM⊥平面PBC,故PC⊥AM ∴ PC⊥平面AMN。 |
15. C
[分析解答]
f(x)=f(20-x)
=-f(20+x)
=-f(-x)=f(40+x)
二、
16. -84
[分析解答]
C![]() X
X![]() ·(-1)
·(-1)![]() ·x
·x![]() =(-1)
=(-1)![]() ·C
·C![]() ·X
·X![]()
令r=3,则得系数(-1)![]() ·C
·C![]() =-84
=-84
17. 3
[分析解答]
y![]() =4x
=4x
=> y![]() -2y+2m=0
-2y+2m=0
y=2x+m
45=(1+![]() )[4-8m] => m=-4 F(1,0)到直线之距离
)[4-8m] => m=-4 F(1,0)到直线之距离 ![]()
∴ ![]()
18. A
[分析解答]
设PA⊥α于A,PB⊥β于B
![]()
![]()
19. B
[分析解答]
1<m<9
原不等式 <==> x![]() +mx > 3x-m
+mx > 3x-m
<==>x![]() -(3-m)x+m > 0
-(3-m)x+m > 0
△=(3-m)
![]() -4m < 0 => 1< m < 9
-4m < 0 => 1< m < 9
三、
20. (1) C (2) B
[分析解答] 依题意
(z4-z1)+(z2-z1)=z3-z1
∴ z4=z3+z1-z2
=1+i+3+3i-4-2i
=2i
解(2)
arg(z4)=![]()
21. A
[分析解答] y=1-cos![]() x+2sinxcosx+3cos
x+2sinxcosx+3cos![]() x
x
=sin2x+cos2x+2 =![]()
令![]() 得:
得:![]() k∈Z
k∈Z
这就是竖直对称轴的一般方程。
22. (1) D (2) C
[分析解答]
易知BD=CD=a过A作AO⊥BC于O,则AO平分BC,且AO⊥平面BCD,过P作PH∥AO交BC于H点,则PH⊥平面BCD。过H作HM∥DC交BD于M ∵CD⊥BD ∴HM⊥BD 连PM,则PM⊥BD
∴∠PMH是二面角P—BD—C的平面角
且S![]() ·a·PM 设PH=HC=x,MH=y
·a·PM 设PH=HC=x,MH=y
则 ![]() ∴
∴
![]() ,
,
∴![]()
![]()
![]()
![]()
∴当![]() 时,PM最短,
时,PM最短,![]()
此时,![]()
∴ 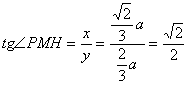
![]()
故△PBD面积最小时,二面角P—BD—C的正切值为![]()
此时,△PBD的面积为![]()
23.( 29 )、( 1 )、( C )。
[分析解答]:设投资于甲商品x万元,总利润为y万元则
![]() (0≤x≤30)
(0≤x≤30)
令 ![]() ,(0≤t≤
,(0≤t≤![]() ) 则 t
) 则 t![]() =30-x x=30-t
=30-x x=30-t![]()
∴ ![]()
![]()
![]()
可见,t=1时,y最大 t=1时,x=29
故投资甲商品29万元,投资乙商品1万元,所获利润最大,最大利润为![]() 万元。
万元。
24. (1) A
[分析解答]:设A(-a,0),B(a,0),P(x0,y0),C(x1,y1),D(x2,y2)
∵△ACD和△PCD面积相等, ∴C是AP中点
故![]()
![]()
∵C在C1上,P在C2上。 ∴ ![]()
![]()
消去y0,得![]() 解之,得x0=2a ( x0=-a舍)
解之,得x0=2a ( x0=-a舍)
于是![]() 故P点坐标为
故P点坐标为![]()
![]()
∴PB方程为![]()
代入C1中:2x![]() -3ax+a
-3ax+a![]() =0 解之,得
=0 解之,得![]() (x2=a舍)
(x2=a舍)
而![]() ∴直线CD的倾斜角为
∴直线CD的倾斜角为![]() 。
。
(2) D
[分析解答]:当CD:x=![]() 过右焦点时,
过右焦点时,
对C1而言:a=2c b![]() =4c
=4c![]() -c
-c![]() =3c
=3c![]() =
=![]()
对C2而言:C![]() =a
=a![]() +b
+b![]() =a
=a![]() +
+![]()
∴ ![]() ,
, ![]()
25.
(1) 对、错、对。
[分析解答]:
由an=a·an-1知,{an}是等比数列,首项与公比都是a,
故an=a![]()
b2=b·a1+c·b1=b·a+c·b=b(a+c)
b3=b·a2+c·b2=b·a![]() +c·b=b(a+c)
+c·b=b(a+c)
=b(a![]() +a·c+c
+a·c+c![]() )
)
b4=b·a3+c·b3=b·a![]() +c·b(a
+c·b(a![]() +ac+c
+ac+c![]() )
)
=b(a![]() +a
+a![]() c+ac
c+ac![]() +c
+c![]() )
)
(2) [分析解答] 猜想
bn=b(a![]() +a
+a![]() ·c+a
·c+a![]() ·c
·c![]() +…+c
+…+c![]() )
)
n=1时,显然成立;
设n=k时,设bk=b(a![]() …+
…+![]() )
)
则n=k+1时 bk+1=b·ak+c·bk
=b·a![]() +cb(a
+cb(a![]() +a
+a![]() c+…+c
c+…+c![]() )
)
![]() …+
…+![]() )
)
故对于一切n∈N,有
![]() …
…![]()
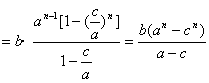
(3) [分析解答]
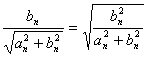
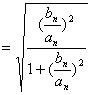
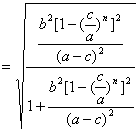
∴![]()