数学文科:模拟试卷四
一、选择题
1. 设M、N是两个非空集合,且M={a|a∈N},则M、N 间的关系为( )
(A) M=N (B) M是N的真子集
(C) M是N的子集 (D) M∈N
2. 两异面直线a、b分别在平面α、β上,若α∩β=c,当a与c相交时,b与c( )
(A)不相交 (B)必相交
(C)相交但不过a与c的交点 (D)相交或平行
3. 双曲线 ![]() 的焦点的坐标是( )
的焦点的坐标是( )
(A) ( ±![]() ,0)
(B) (±
,0)
(B) (±![]() ,0)
,0)
(C) ( 0,±![]() )
(D) (0,±
)
(D) (0,±![]() )
)
4. 设向量![]() 对应复数
对应复数 ![]() ,把
,把 ![]() 旋转一个锐角后,得向量
旋转一个锐角后,得向量![]() ,
,
若![]() 对应复数
对应复数 ![]() ,则
,则![]() 需( )
需( )
(A) 逆时针旋转60° (B) 顺时针旋转60°
(C) 逆时针旋转30° (D) 顺时针旋转30°
5. 已知二次函数f(x)的图象是一条开口向下的抛物线,且对任意x∈R,均有f(1-x)=f(1+x)
成立。下列不等式中正确的是( )
(A) ![]() (B) f(-1)>f(2)
(B) f(-1)>f(2)
(C) f(-1)<f(2) (D) f(0)<0
6. 函数 ![]() 的单调递增区间是(k∈Z) ( )
的单调递增区间是(k∈Z) ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7. 命题甲:在数列{an}中,对任意m、n∈N,m≠n,都有am+1-am=an+1-an成立,
命题乙:{an}是等差数列,则甲是乙的( )
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 非充分且非必要条件
8. 函数 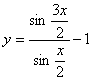 的最小正周期为( )
的最小正周期为( )
(A) ![]() (B)
π
(B)
π
(C) 2π
(D) ![]()
9. 椭圆 ![]() 与双曲线
与双曲线 ![]() 有相同的焦点F1、F2,P是它们的一个
有相同的焦点F1、F2,P是它们的一个
公共点,则|PF1|·|PF2|的值为( )
(A) m-a![]() (B)
(B) ![]()
(C) m![]() -a
-a![]() (D) m-a
(D) m-a
10. 若sinθ、cosθ是方程 4x![]() +2mx+m=0 的两个根,则 m 的值为( )
+2mx+m=0 的两个根,则 m 的值为( )
(A) m∈[![]() ,0) (B)
,0) (B)
![]()
(C) ![]() (D)
(D)
![]()
11. 在原坐标系中,抛物线C的方程为 y![]() =-4x,若在移轴后的新坐标系中,它的方
=-4x,若在移轴后的新坐标系中,它的方
程变为 y'![]() +4x'-4y'=0,则新坐标的原点O'的原坐标为( )
+4x'-4y'=0,则新坐标的原点O'的原坐标为( )
(A) (-1,-2) (B) (1,-2)
(C) (0,2) (D) (2,-1)
12. f(x)是减函数,且f(ax+3)=x(a≠0)。若f(x)的反函数 f![]() (x) 的定义域为
(x) 的定义域为![]() ,
,
则f(x)的定义域为( )
(A) [1,4] (B) [a,2a]
(C) [4,7] (D) [2a,a]
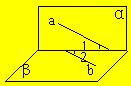
| 13. 如图,直线a在α内,b在β内,α⊥β,α∩β=c,∠1=∠2=60°则a、b所成角θ的
余弦值为( ) |
(A) 1
(B)![]()
(C) ![]() (D)
(D)![]()
14. 从0,1,2,3,4,5这六个数中,任取两个作除法,可得出不同的锐角的正弦
值的个数为( )
(A) 15 (B) 11
(C) 10 (D) 9
15. 已知α是方程lg(x+1)+lg2x-2lg2=lg(5x-9)的根,则无穷数列1, ![]()
…的各项和为( )
(A) ![]() 或-5
(B)
或-5
(B) ![]()
(C) -5
(D) ![]() 或不存在
或不存在
二、填空题
16. 若三个数a、b、c成等差数列,a、c、b成等比数列,则a:b:c=( )
(A)3:2:1或4:1:(-2) (B)1:1:1或4:1:(-2)
(C)1:2:3或4:1:(-2) (D)1:1:1或3:1:(-2)
[分析解答]
17. 等边圆锥(轴截面为正三角形)的底圆半径为 ![]() ,它的内切球与圆锥侧面切于球的
,它的内切球与圆锥侧面切于球的
一个小圆,则以这小圆为底的球的两个球冠的面积分别为( )
(A)5πcm![]() 或7πcm
或7πcm![]() (B)5πcm
(B)5πcm![]() 或6πcm
或6πcm![]()
(C)πcm![]() 或3πcm
或3πcm![]() (D)5πcm
(D)5πcm![]() 或9πcm
或9πcm![]()
18.![]() [
[![]() ]=
]=
( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
19. 函数 y=(x![]() +2x+2)
+2x+2) ![]() +2(x
+2(x![]() +2x+2)-3,
+2x+2)-3,
当x=( )时,y取最小值为( )。
[分析解答]
三、解答题:
20. 已知复数z满足条件:|![]() |=
|=![]() ,且arg
,且arg![]() ,求z的值为( )
,求z的值为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
[分析解答]
21. 已知cosα=a,cosβ=b,a+b≠0其中α是第一象限角,β是第二象限角,若角γ满足
条件:![]() ,求tgγ的值( )。
,求tgγ的值( )。
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D) ![]()
[分析解答]
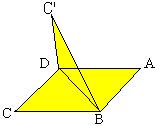
22. 已知ABCD,AB=2![]() ,BC=
,BC=![]() ,∠A=60°,把△DBC沿BD折起为△DBC'。
,∠A=60°,把△DBC沿BD折起为△DBC'。
(1) 求证:不论C'点在何位置,异面直线AD与C'B所成角与二面角C'—BD—C的
平面角相等或互补;
[分析解答]
|
(2) 当二面角C'—BD—C为30°时,求三棱锥C'—BDC的体积。
|
[分析解答]
23. 某商店有甲商品100件,乙商品50件,甲单价是乙单价的一半,现各卖出25件后,为使乙商品不滞销,商店对甲、乙商品同时调价相同的百分数,若将甲商品提价20%,乙商品降价20%,则两种商品剩余件数的平均价格下降2元,为使甲、乙两种商品原来的平均价格不变,
甲提价和乙降价的相同的百分数应该是多少? ( )
(A) 55.55% (B) 33.33%
(C) 44.44% (D) 66.66%
甲、乙两商品原价为多少? ( )
(A)甲:80元/件; 乙:110元/件 (B) 甲:120元/件; 乙:60元/件
(C)甲:60元/件; 乙:120元/件 (D) 甲:50元/件; 乙:100元/件
[分析解答]
24. 已知二次函数
f(x)=a(a+1)x![]() -(2a+1)x+1
-(2a+1)x+1
(1) 求函数f(x)的图象截x轴所得弦长;( $S*D$ )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
[分析解答]
(2) 用数学归纳法证明:当a依次取值1,2,3,4…n时,f(x)图象截x轴所得n条
弦长之和是 ![]() 。
。
[分析解答]
25. 已知锐角∠AOB=a,边OA、OB上分别有点P、Q,且△OPQ的面积为定值:S=8。当P、Q分
别在OA、OB上运动时,求PQ中点M的轨迹方程,并求|OM|的最小值。( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[分析解答]
参 考 答 案
一、
1. C
2. D
[分析解答]
注意b、c共面
3. D
[分析解答]
注意焦点在y轴上,c![]() =13
=13
4. B
[分析解答]
求出![]() 和
和![]() 的夹角θ:tgθ
的夹角θ:tgθ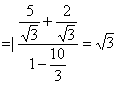
5. C
[分析解答]
注意图象对称轴为x=1
6. D
[分析解答] ![]()
令 2kπ+π≤2x+![]() ≤2kπ+2π而得
≤2kπ+2π而得
7. C
[分析解答]
根据定义去检验
8. C
[分析解答]
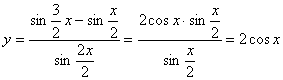
9. A
[分析解答]
4c![]() =PF
=PF![]() +PF
+PF![]() -2PF1·PF2cosθ
-2PF1·PF2cosθ
=(PF1+PF2)
![]() -2PF1·PF2·(1+cosθ)
-2PF1·PF2·(1+cosθ)
=4m-2|PF1·PF2|·2sin![]() (
(![]() )
)
4c![]() =(PF1-PF2)
=(PF1-PF2) ![]() +2|PF1·PF2|·(1-cosθ)
+2|PF1·PF2|·(1-cosθ)
=4a![]() +2|PF1·PF2|·2cos
+2|PF1·PF2|·2cos![]() (
(![]() )
)
相减:0=4a![]() -4m+4|PF1·PF2|
-4m+4|PF1·PF2|
∴ |PF1|·|PF2|=m-a![]()
10. B
[分析解答]
sinθ+cosθ=![]() m
m![]() -2m-4=0
-2m-4=0
=>
=> ![]()
sinθ* cosθ=![]() m
m![]() -4m≥0
-4m≥0
11. A
[分析解答]
(y'-2) ![]() =-4(x'-1)
=-4(x'-1)
∴O'(-1,-2)
12. C
[分析解答]
设t=ax+3,则 ![]() ∴
∴ ![]()
![]() ≤
≤![]() ≤
≤ ![]()
=> 4≤t≤7
a<0
13. C
[分析解答]
平移相交,利用余弦定理。
14. C
15. D
[分析解答] lg(x+1)+lg2x-2lg2=lg(5x-9)
=> ![]() x1=3,
x2=6
x1=3,
x2=6
若x=3,则 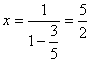 ,若x=6,则S不存在。
,若x=6,则S不存在。
二、
16. B
[分析解答]
a+c=2b
=> a![]() -5ab+4b
-5ab+4b![]() =0 => a=b=c或a=4b,c=-2b
=0 => a=b=c或a=4b,c=-2b
a·b=c![]()
17. C
[分析解答]
球半径r=1,球冠之高分别为 ![]() 和
和 ![]()
18. D
[分析解答]
原式 =![]()
![]()
19. ( -1 ), ( 0 )
[分析解答]
x=-1,y最小值为0
设t=x![]() +2x+2,则t≥1(x=-1时取等号)
+2x+2,则t≥1(x=-1时取等号)
y=t![]() +2t-3=(t+1)
+2t-3=(t+1) ![]() -4
-4
故x=-1时,y![]() =0
=0
三、
20. A
[分析解答]
由已知|![]() |=
|=![]() ,
, ![]()
∴![]()
∴![]()
∴ ![]() ∴
∴ ![]()
21. B
[分析解答]
∵tg![]() =tg
=tg![]() ·tg
·tg![]()
∴ 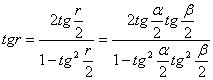
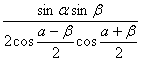
![]()
(∵cosα+cosβ=a+b≠0)
∵cosα=a, cosβ=b, α是第一象限角,β是第二象限角。
∴![]() , sinβ=
, sinβ=![]()
∴![]()
22. (1)
[分析解答]
证明:在△ABD中,AB=2![]() ,AD=BC=
,AD=BC=![]() ,∠A=60°
,∠A=60°
∴BD![]() =AB
=AB![]() +AD
+AD![]() -2AB·ADcos∠A
-2AB·ADcos∠A
![]() 60° =9
60° =9
又∵AB![]() -AD
-AD![]() =
=![]() -(
-(![]() )
)![]() =9
=9
∴BD![]() =AB
=AB![]() -AD
-AD![]() ,即BD
,即BD![]() +AD
+AD![]() =AB
=AB![]()
∴△ABD是直角三角形,∠ADB=90°
∴∠CBD=90°,BD⊥BC, ∵∠C'BD=∠CBD=90°,∴BD⊥BC'
∴∠C'BC是二面角C'—BD—C的平面角,又∵BC∥AD,
∴∠C'BC是异面直线AD与C'B所成角或其补角,命题得证。
(2) [分析解答]
由(1)得BD⊥BC,BD⊥BC',BC∩BC'=B,
∴BD⊥平面BCC', BD为三棱锥D—CBC'的高,BD=3.
由(1)得∠C'BC是二面角C'—BD—C的平面角,
∴∠C'BC=30 ∴S![]() =
= ![]() ·BC·BC'·sin30°=
·BC·BC'·sin30°=![]()
∴V![]() _ = V
_ = V![]() =
= ![]() S
S![]() ·BD =
·BD = ![]()
23. B; C
[分析解答]
设甲商品原价格为a元,则乙商品原价格为2a元,甲提价与乙降价的相同
百分数为x,甲、乙商品原平均价格 ![]()
甲提价20%,乙降价20%后剩余件数的平均价格![]()
甲提价x,乙降价x后,剩余件数的平均价格![]()
由已知![]() ∴ x=
∴ x=![]() ≈33.33%
≈33.33%
又由已知![]() ∴a=60, ∴2a=120
∴a=60, ∴2a=120
答:甲商品提价33.33%,乙商品降价33.33%平均价格不变;甲商品原价60元/件,
乙商品原价120元/件。
24. (1) D
[分析解答]
设f(x)的图象交x轴于两点A(x1,0),B(x2,0),则x1,x2为一元二次方程
a(a+1)x![]() -(2a+1)x+1=0的两实根。(由已知a(a+1)≠0)
-(2a+1)x+1=0的两实根。(由已知a(a+1)≠0)
△ = (2a+1) ![]() -4a(a+1)=1>0
-4a(a+1)=1>0
∴x1、x2是两不等实根。
x1+x2=![]() ,
, ![]()
∴|AB|=|x1-
x2|=![]()
![]()
∴|AB|= ![]() 为所求弦长
为所求弦长
(2) [分析解答]
证明:当a=1,2,3,4,…n时,弦长11=![]() ,l2 =
,l2 = ![]()
(i)当n=1时S1=l1=![]() ∴当n=1时,等式成立
∴当n=1时,等式成立
(ii)假设当n=k(k∈N)时,等式成立
即Sk=![]() 则当n=k+1时
则当n=k+1时
Sk+1=Sk+lk+1
![]()
![]()
![]()
∴ 当n=k+1时,等式成立。由(i)(ii)对任意n∈N, ![]() 均成立。
均成立。
25. B
[分析解答] 以O为原点,OA为x轴,建立直角坐标系xOy ∵在x轴正半轴上,
∴设P(x1,0)(x1>0) 又∵Q在OB上,∠AOB=a为锐角,
∴Q点在第一象限,设 Q(x2,y2),射线OB的方程y=xtga,
∴y2=x2tga (1)式
∴![]() |OP|·|y2|
|OP|·|y2|
![]()
∴![]() 设PQ中点M(x,y)(x>0,y>0)
设PQ中点M(x,y)(x>0,y>0)
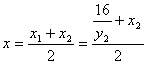
![]()
![]()
∴ 代入(1)式得
y2=2y
![]() 即 y
即 y![]() -xytga+4tga=0(x>0,y>0)为所示M点的轨迹方程。
-xytga+4tga=0(x>0,y>0)为所示M点的轨迹方程。
由上述方程,得:x=yctga+![]()
∴|OM|![]()
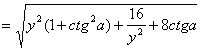
∵y![]() (1+ctg
(1+ctg![]() a)>0,
a)>0,![]() >0
>0
∴![]() ≥
≥ ![]() (∵a为锐角csca>0)
(∵a为锐角csca>0)
∴|OM|≥![]()
![]()
![]()
当 y![]() (1+ctg
(1+ctg![]() a)=
a)=![]() ,即
,即 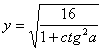 时,式中等号成立。
时,式中等号成立。
∴当y=4sina时,|OM|![]() =
=![]()