数学文科:模拟试卷六
一、选择题
1. 满足条件{0,1}∪A={0,1}的所有集合A的个数是( )
(A) 1个 (B) 2个
(C) 3个 (D) 4个
2. “0.1![]() >1”是“|x|<1”的( )
>1”是“|x|<1”的( )
(A) 充分但不必要条件 (B) 必要但不充分条件
(C) 充分且必要条件 (D) 既不充分又不必要条件
3. 使得式子![]() 有意义的x的取值范围是( )
有意义的x的取值范围是( )
(A) ![]() 且x≠kπ,k∈Z}
且x≠kπ,k∈Z}
(B) {![]() 且x≠2kπ+
且x≠2kπ+![]() ,k∈Z}
,k∈Z}
(C) {x|kπ+![]() <x<kπ+
<x<kπ+![]() 且x≠kπ+
且x≠kπ+![]() ,k∈Z}
,k∈Z}
(D) {x|![]() 且x≠
且x≠![]() ,k∈Z}
,k∈Z}
4. 复数2+i和3+i的辐角主值分别为α、β则α+β等于( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
5. 在棱长为a的正方体ABCD—A1B1C1D1中,M是BB1的中点,则异面直线BD1和AM所成角的余弦值等于( )
(A) ![]() (B)
(B)
![]() (C)
(C) ![]() (D)
(D)
![]()
6. 为得到函数y=sin2x的图象,需将函数![]() 的图象( )
的图象( )
(A) 向左平移![]() (B) 向右平移
(B) 向右平移![]()
(C) 向左平移![]() (D) 向右平移
(D) 向右平移![]()
7. 双曲线![]() 的两焦点的坐标为( )
的两焦点的坐标为( )
(A) (0,5),(0,-5) (B) (5,0),(-5,0)
(C) (2,4),(2,-6) (D) (7,-1),(-3,-1)
8. 化简![]() 得( )
得( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
9. 棱长均为a的正三棱柱ABC—A1B1C1中,M为A1B1的中点,则M到BC的距离为( )
(A) ![]() (B)
(B)
![]() (C)
(C) ![]() (D)
(D)![]()
10. 已知实数x、y、z依次成等差数列,x+y+z=12且x、y、y+z依次成等比数列,
则x的值为( )
(A) 2 (B) 8
(C) 2或8 (D) 2或-8
11. 和圆x![]() +y
+y![]() =1相外切并且又和x轴相切的动圆圆心的轨迹方程是( )
=1相外切并且又和x轴相切的动圆圆心的轨迹方程是( )
(A) x![]() =2y+1
(B) x
=2y+1
(B) x![]() =2|y|+1
=2|y|+1
(C) x![]() =-2y+1
(D) x
=-2y+1
(D) x![]() =2y-1
=2y-1
12. 一个无穷等比数列各项之和为![]() ,则这个数列的各项平方和为( )
,则这个数列的各项平方和为( )
(A) ![]() B)
B)
![]() (C)
(C) ![]() (D)
(D) ![]()
13. 椭圆![]() 与曲线
与曲线![]() (k<25且k≠9)的焦距分别为d1和d2,
(k<25且k≠9)的焦距分别为d1和d2,
则d1和d2的大小关系是( )
(A) d1 > d2 (B) d1 < d2
(C) d1=d2 (D) 不能确定的
14. 已知数列{a![]() }的前n项和S
}的前n项和S![]() =n
=n![]() ,
,
则![]() 的值为( )
的值为( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
15. 圆x![]() +y
+y![]() +2x+4y-3=0上到直线x+y+1=0的距离等于
+2x+4y-3=0上到直线x+y+1=0的距离等于![]() 的点有( )
的点有( )
(A) 1个 (B) 2个
(C) 3个 (D) 4个
二、填空题:
16. 已知![]() <1 则 a 的取值范围是( )。
<1 则 a 的取值范围是( )。
(A)a≥1或0<a<1
(B)a>1或0<a<![]()
(C)a>1或0≤a<1 (D)a<1或0<a<1
[分析解答]
17. ![]() 的值等于( )。
的值等于( )。
(A) ![]() (B)
(B)
![]() (C)
(C) ![]() (D) -2
(D) -2
[分析解答]
18. 若sinα·cosβ=1,则![]() 的值等于( )。
的值等于( )。
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
[分析解答]
19. 函数f(x)是定义在(-∞,+∞)上的偶函数,且f(1+x)=f(1-x),当-1≤x≤0时
![]() ,则f(8.6)= ( )。
,则f(8.6)= ( )。
[分析解答]
20. 将数字1、2、3、4填入标号为1、2、3、4的四个方格里,每格填一个数字,
则每个方格的标号与所填数字均不相同的填法有( )种。
[分析解答]
三、解答题
21. 解不等式![]() (x-4)>
(x-4)>![]() (x-2)(a>0且a≠1)。
(x-2)(a>0且a≠1)。
[分析解答]
22. 已知a+b+c=1,求![]() 的最大值。( )
的最大值。( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[分析解答]
|
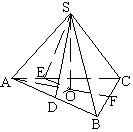
23. 在三棱锥S—ABC中,SA=2,AB=AC, ∠SAB=∠SAC=60°, SA和底面成45°,又SA、AB、BC顺次成等差数列. (1) 求证:SA⊥BC; (2) 求二面角S—BC—A的大小( )。 (A)
(C) |
[分析解答]
24. 果园里种了30棵苹果树,平均每棵每年产400个苹果,根据统计,在这个果园内每加种一棵苹果树,则平均每棵树的年产量减少10个,问应加种( $W*5$ )棵才能使年产量最高?
[分析解答]
25. 等差数列{an}和等比数列{bn}中,它们各项都是正数,已知a1=b1,ak=bk,
k≥2,试证明若n>k时,an≤bn;若1≤n≤k时,an≥bn。
[分析解答]
26. 已知椭圆C:![]() (a>b>0)上有A、B两点,直线l:y=x+k上有C、D两点,且ABCD是正方形。若正方形ABCD的外接圆方程为x
(a>b>0)上有A、B两点,直线l:y=x+k上有C、D两点,且ABCD是正方形。若正方形ABCD的外接圆方程为x![]() +y
+y![]() -2y-8=0,求椭圆C和直线l的方程。
-2y-8=0,求椭圆C和直线l的方程。
(1) 求椭圆C的方程C: ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2) 求直线l的方程l: ( )
(A)x+y-4=0 (B)x-y+4=0 (C)x-y-4=0 (D)x+y+4=0
[分析解答]
参 考 答 案
一、
1. D
[分析解答]
A=ф,A={0},A={1},={0,1}
2. A
[分析解答]
lgx![]() <0 => |x|<1且x≠0
<0 => |x|<1且x≠0
3. C
[分析解答] cosx≠0
![]() <cosx<
<cosx<![]() => kπ+
=> kπ+![]() < x < kπ+
< x < kπ+![]() 且x≠kπ+
且x≠kπ+![]() ,k∈Z
,k∈Z
4. C
[分析解答]
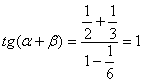
5. D
[分析解答]
在正方体的下方再拼上一个完全一样的正方体。
6. D
[分析解答]
![]()
∴sin2x左移![]() 得
得![]() ,现反之。
,现反之。
7. C
[分析解答]
注意中心为O'(2,-1),c=5,焦点在直线x=2上。
8. B
[分析解答]
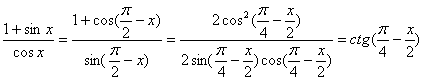
9. A
[分析解答]
转化为在边长分别为![]() 、
、![]() 、a的三角形中求a边上的高。
、a的三角形中求a边上的高。
10. C
[分析解答]
x+z=2y
x+y+z=12 => x=2或8
x(z+2)=y![]()
11. B
[分析解答]
设圆心为(x,y)则![]() =1+|y|
=1+|y|
12. A
[分析解答]
平方和组成首项为![]() ,公比为q
,公比为q![]() 的无穷等比数列
的无穷等比数列
13. C
[分析解答]
d1=8,而![]() (k<9时)
(k<9时)
或![]() (9 < k < 25时)
(9 < k < 25时)
14. B
[分析解答] 由![]() 知
知![]() ,
,
原式 = 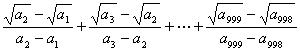
![]()
15. C
[分析解答]
和x+y+1=0距离等于![]() 的直线为x+y-1=0或x+y+3=0考虑这两条直线与圆的交点个数。
的直线为x+y-1=0或x+y+3=0考虑这两条直线与圆的交点个数。
二、
16. B
[分析解答] a>1或0<a<![]()
a>1
0<a<![]()
loga ![]() <loga
a =>
或
<loga
a =>
或
![]() <a
<a
![]() >a
>a
17. B
[分析解答]
![]()
原式= 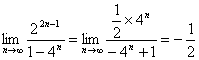
18. C
[分析解答]
![]()
sinα=1 sinα=-1
sinα·cosβ=1 => 或
cosβ=1 cosβ=-1
19. ( 0.3 )
[分析解答]
0.3
f(1+x)=f(1-x) => f(x)=f(2-x)
又f(x)为偶函数,故f(2-x)=f(2+x)
∴f(x)=f(2+x)于是f(8.6)=f(0.6)=f(-0.6)=0.3
20. ( 9 )种
[分析解答]
9种
具体去排一下,可得九种不同排法。
三、
21.
[分析解答]
x-4>0
依题意可知 则有x>4.当0<a<1时,
x-2>0
由![]() (x-4)
(x-4)![]() >
>![]() (x-2),
(x-2),
得到(x-4)![]() <(x-2),
<(x-2),
则有x![]() -9x+18<0,解得3<x<6
-9x+18<0,解得3<x<6
x>4,
由 得到4<x<6
3<x<6,
当a>1时,由![]() (x-4)
(x-4)![]() >
>![]() (x-2),得到(x-4)
(x-2),得到(x-4)![]() >(x-2),
>(x-2),
即x![]() -9x+18>0,解得x<3或x>6
-9x+18>0,解得x<3或x>6
x>4
由 得到x>6
x<3或x>6,
∴当0<a<1时,原不等式的解集为{x|4<x<6};当a>1时,原不等式的解集
为{x|x>6}.
22. C
[分析解答]
证明:设![]() ,
,
则![]()
∵a+b+c=1
∴![]()
∵![]() ≤3a+1+3b+1=3(a+b)+2,
≤3a+1+3b+1=3(a+b)+2,
![]() ≤3a+1+3c+1=3(a+c)+2,
≤3a+1+3c+1=3(a+c)+2,
![]() ≤3b+1+3c+1=3(b+c)+2,
≤3b+1+3c+1=3(b+c)+2,
等号成立的条件是a=b=c,
∴![]() ≤6+3(a+b)+2+3(a+c)+2+3(b+c)+2 =12+6(a+b+c)=18,
≤6+3(a+b)+2+3(a+c)+2+3(b+c)+2 =12+6(a+b+c)=18,
∴u≤![]() ,当a=b=c时,u取得最大值
,当a=b=c时,u取得最大值![]()
23.
|
[分析解答] 如图,过S作SO⊥底面ABC,过O分别作OD⊥AB, OE⊥AC,分别连结SD和SE, 则OD和OE分别是SD和 SE在底面ABC上的射影,则SD⊥AB,SE⊥AC。 在Rt△SAD和Rt△SAE中 ∵SA=SA,∠SAE=∠SAD,∠SDA =∠SEA=90°,∴Rt△SAD≌Rt△SAE,
∴AD=AE.在Rt △OAD和Rt△OAE中,OA=OA,∠ODA=∠OEA,AD=AE, ∴Rt△OAD≌Rt△OAE, ∴∠OAD=∠OEA,延长OA,使其延长线交BC于F,∵△ABC中, AB=AC,∴AF⊥BC。 连结SF,则直线AF既是直线SF在平面ABC上的射影, 又是直线SA在平面ABC上的射影。 ∵AF⊥BC,∴SA⊥BC且SF⊥BC, ∴∠SFA是二面角S-BC-A的平面角。 |
在Rt△SAD中,SA=2,∠SAD=60°, ∴AD=1.在Rt△SAO中,
∵AO是SA在底面ABC上的射影, ∴∠SAO是SA和底面ABC所成的角,
∴∠SAO=45°,∵SA=2, ∴ ![]() 。
。
在Rt△AOD中,∠ODA=90°,AD=1,AO=![]() ,
,
∴∠OAD=45°,同理∠OAE=45°, ∴∠BAC=90°,设AB=a,则
SA+BC=2a,∵△ABC是等腰Rt△. ∴ ![]()
∴![]() ,∴
,∴ ![]() ,
,
∴![]() 在Rt△ABF中,∵
在Rt△ABF中,∵ ![]() , ∴
, ∴![]() ,
,
∵![]() , ∴ OF=1,∴tg∠SFO=
, ∴ OF=1,∴tg∠SFO=![]() ,
,
∠SFO=arctg![]() ,即二面 角S—BC—A等于arctg
,即二面 角S—BC—A等于arctg![]() 。
。
24. ( 5 )
[分析解答] 设种x棵树时,年总产y个苹果。
则有y=(30+x)(400-10x)
=12000+100x-10x![]()
=12000-10(x![]() -10x)=12000-10(x-5)
-10x)=12000-10(x-5) ![]() +250
+250
=12250-10(x-5) ![]()
当x=5时,y![]() =12250(个)。因此,加种5棵苹果树时,年总产量最大。
=12250(个)。因此,加种5棵苹果树时,年总产量最大。
25.
[分析解答]
证明:由等差数列各项为正数,可知a1>0,公差d≥0;由等比数列各
项为正数,可知b1>0,公比q>0.由a1=b1,ak=bk,则有
a1+(k-1)d=b1q![]() =a1q
=a1q![]() , ∴
, ∴ ![]() ∵d≥0,∴q
∵d≥0,∴q![]() -1≥0,∴q≥1
-1≥0,∴q≥1
设q=1+a(a≥0),由an+1-bn+1=(a1+nd)-b1q![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
由此可以看出:当1≤n≤k-1时,a![]() ≥b
≥b![]() ,
,
即n≤k时,an≥bn;当n>k-1时,a![]() ≤b
≤b![]() ,即n>k时,an≤bn。
,即n>k时,an≤bn。
26.
(1) B
(2) B
[分析解答]
∵已知外接圆为x![]() +(y-1)
+(y-1) ![]() =9,则圆心P为(0,1),半径r=3,正方形边长
=9,则圆心P为(0,1),半径r=3,正方形边长![]() ,由P到l的距离为
,由P到l的距离为![]() ,得到
,得到![]() ,k=4或k=-2。
,k=4或k=-2。
x![]() +y
+y![]() -2y-8=0
-2y-8=0
(1)当k=4时, 解之,得到C(0,4),D(-3,1)。
y=x+4.
∵A和C关于P对称,∴C(0,-2),同样可以得出D的坐标为(3,1)。
![]() ,
,
∵A、B是椭圆C上的点,则有
a![]() =12,b
=12,b![]() =4,
=4,
![]()
∴椭圆![]() ,直线l:y=x+4.
,直线l:y=x+4.
x![]() +y
+y![]() -2y-8=0
-2y-8=0
当k=-2时, 解之,得到C(0,-2),D(3,1)。
y=x-2,
∵A、C关于P对称,∴A(0,4),同样,可以求得B的坐标为(-3,1).
![]() ,
,
依题意,有
解之,得![]() ,b
,b![]() =16.
=16.
![]() .
.
∵a<b,∴舍去此解。∴所求椭圆![]() ,直线l:x-y+4=0。
,直线l:x-y+4=0。