数学文科:模拟试卷七
一、选择题:
1. 已知集合A={x|x=2n-1,n∈N且n<10},B={y|y=4n-1,n∈N且n<10},
那么A∩B的真子集的个数是( )
(A) 17 (B) 16
(C) 15 (D) 14
2. 以下四个函数中,在区间(-∞,0)上是增函数的函数是( )
(A) ![]() (B) y=-(x+1)
(B) y=-(x+1)![]()
(C) y=x![]() +1
(D)
+1
(D) ![]()
3. 若函数lg(f(x)·g(x))的定义域为集合A,函数lg(f(x))的定义域为集合B,
lg(g(x))的定义域为集合C,则A、B、C之间的关系是( )
(A) A=B=C (B) A=(B∪C)
(C) A=(B∩C) (D) 以上答案都不对
4. ![]() 等于( )
等于( )
(A)cos2-sin2 (B)-cos2-sin2
(C)-cos2+sin2 (D)cos2+sin2
5. 在等腰Rt△ABC中,AB=BC=1,M是AC的中点,沿BM把它折为二面角,
折后A与C的距离等于1,则二面角C—BM—A的大小等于( )
(A) 30° (B) 60°
(C) 90° (D) 120°
6. 在以下四对不等式中,解集相同的是( )
(A) x![]() -3x+2>0和
-3x+2>0和![]() >0 (B) sinx>
>0 (B) sinx>![]() 和
和![]() <x<
<x<![]()
(C) 2![]() <1和log2x<1
(D) |log2x|>1和|log
<1和log2x<1
(D) |log2x|>1和|log![]() x|>1
x|>1
7. 圆x![]() +y
+y![]() -4x+2y+c=0与y轴相交于A、B两点,设这个已知圆的圆心为P,
-4x+2y+c=0与y轴相交于A、B两点,设这个已知圆的圆心为P,
且∠APB=90°,则c的值等于( )
(A) -3 (B) 8
(C) 3
(D) ![]()
8. “lga+lgc=2lgb”是“a、b、c依次成等比数列”的( )
(A) 充分但不必要条件 (B) 必要但不充分条件
(C) 充分且必要条件 (D) 既不充分也不必要条件
9. 五个人排成一排,甲与乙不相邻且甲与丙也不相邻的排法有( )
(A) 24种 (B) 36种
(C) 48种 (D) 60种
10. 椭圆![]() 的离心率为
的离心率为![]() ,则k的值是( )
,则k的值是( )
(A) ±4
(B) ![]()
(C) 4或![]() (D) -4或
(D) -4或![]()
11. 在适合以下条件的数列中,是等差数列的是( )
(A) 前n项和Sn=n![]() -n+2
-n+2
(B) 第n项是log2sin![]()
(C) 第n项是![]()
(D) 由某两个等差数列对应的乘积构成的数列
12. 已知△ABC的三条边a、b、c依次成等比数列,那么sinB+cosB的取值范围是( )
(A) ( 1,(![]() ) ]
(B) [
) ]
(B) [ ![]() ]
]
(C) ( ![]() ]
(D) [
]
(D) [ ![]() ,1 ]
,1 ]
13. 若抛物线y=x![]() -2xsinα+1的顶点在椭圆x
-2xsinα+1的顶点在椭圆x![]() +4y
+4y![]() =1上,则这样的抛物线共有( )
=1上,则这样的抛物线共有( )
(A) 1条 (B) 2条
(C) 3条 (D) 4条
14. 如果方程![]() 表示双曲线,那么下列各椭圆中,与已知双曲线共焦点的是
表示双曲线,那么下列各椭圆中,与已知双曲线共焦点的是
( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
15. 若对于任意实数t,函数f(x)=x![]() +mx+n都满足关系式f(2+t)=f(2-t),则有( )
+mx+n都满足关系式f(2+t)=f(2-t),则有( )
(A) f(2) < f(1) < f(4) (B) f(1) < f(2) < f(4)
(C) f(2) < f(4) < f(1) (D) f(4) < f(2) < f(1)
二、填空题:
16. 函数f(x)=sin(2x+φ)的图象的一条对称轴的方程是![]() ,且φ∈(0,π),
,且φ∈(0,π),
则φ=( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[分析解答]
17. 三条直线 a、b、c两两成异面直线,它们互相成等角,且存在一个平面与它们都平行,
则 a 和 b 形成角的大小为( )。
(A)30° (B)90°
(C)60° (D)45°
[分析解答]
18. 函数 ![]() (x∈R)的最小值等于( )
(x∈R)的最小值等于( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[分析解答]
19. ![]() 展开式中,含 x
展开式中,含 x![]() 项的系数等于(
)
项的系数等于(
)
[分析解答]
三、解答题:
20. 解不等式:![]() ≥1。解集为:( )
≥1。解集为:( )
(A) (0, ![]() ]∪[
]∪[ ![]() ,6)
(B) (0,
,6)
(B) (0, ![]() ]∪[
]∪[ ![]() ,3)
,3)
(C) (0, ![]() ]∪[
]∪[ ![]() ,3)
(D) (0,
,3)
(D) (0, ![]() )∪(
)∪( ![]() ,3)
,3)
[分析解答]
21. 已知α,β∈(0,![]() ),且asinα+bcosβ=sinβ,asinβ+bcosα=sinα,
),且asinα+bcosβ=sinβ,asinβ+bcosα=sinα,
![]() 。求证:a
。求证:a![]() =1-b。
=1-b。
[分析解答]
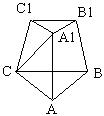
| 22. 在三棱台ABC—A1B1C1中,A1B1是A1C与B1C1的公垂线,已知AB=3cm,
AA1=AC=5cm,二面角A1—AB—C等于60°, |
(1)求三棱锥A1—ABC的体积;( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)求二面角A1—AC—B的大小。( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[分析解答]
23. 无盖的圆柱形铁桶的容积是![]() ,用来做桶底的铁皮每平方米的价格为3元,做侧面的铁皮每平方米价格为2元,问桶高和底面半径选择怎样的长度时,才能使得做一个铁桶的成本最低?
,用来做桶底的铁皮每平方米的价格为3元,做侧面的铁皮每平方米价格为2元,问桶高和底面半径选择怎样的长度时,才能使得做一个铁桶的成本最低?
[分析解答]
24. 过点M(-1,0)的直线l1与抛物线y![]() =4x交于P1和P2两点,P是P1P2的中点,过点P和
=4x交于P1和P2两点,P是P1P2的中点,过点P和
这个抛物线焦点的直线为l2,若l1的斜率为k,试把直线l2的斜率与直线l1的斜率的
比表示为k的函数,并指出这个函数的定义域及单调区间,并说明在每一个单调区间上
是增函数还是减函数。
[分析解答]
25. 设数列z1,z2,…,zn,… 是首项为48,公比为 ![]() 的等比数列。
的等比数列。
(1) 求z4;( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[分析解答]
(2) 将这个数列的实数项不改变原来的次序,从首项开始,排成a1,a2,…,an,…,
试求a3;( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
[分析解答]
(3) 求所得的实数数列 {an} 的各项和。( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[分析解答]
参 考 答 案
一、
1. C
[分析解答]
A={1,3,5,7,9,11,13,15,17} B={3,7,11,15,19,23,27,31,35}
A∩B={3,7,11,15}
真子集2![]() -1=15
-1=15
2. D
[分析解答]
逐个选项一一检查。
3. D
4. B
[分析解答]
原式=|cos2|-|sin2|=-cos2-sin2
5. C
[分析解答]

6. D
[分析解答]
很显然(A)、(B)、(C)不合要求
7. A
[分析解答]
注意弦长、弦心距、半径的关系而得![]()
8. A
[分析解答]
注意a、b、c成等比,不一定有lga+lgc=2lgb
9. B
[分析解答]
按甲的可能位置分类讨论
10. C
[分析解答]
注意k>1时,a![]() =k+8
=k+8
-8<k<1时,a![]() =9
=9
11. B
[分析解答]
注意考查通项公式是否是n的一次函数。
12. A
[分析解答]
根据b![]() =ac,及
=ac,及![]() 求出0<B≤
求出0<B≤![]()
13. D
[分析解答]
把顶点坐标(sinα,cos![]() α)代入椭圆方程
α)代入椭圆方程
14. B
[分析解答]
当p<0,q<0时 c![]() =-p-q
=-p-q
15. A
[分析解答]
注意x=2是函数的图象的对称轴。
二、
16. D
[分析解答]
2×![]() +φ=
+φ=![]() => φ=
=> φ=![]()
17. C
[分析解答] 60°
在平面内取一点O,过O有平面内的直线 a'、b'、c',分别平行于 a、b、c
且 a'、b'、c'两两所成角相等。
18. D
[分析解答]
![]()
![]()
19. -280
[分析解答] -280
![]() ·
·![]() ·
·![]() = (-2)
= (-2)![]() ·
·![]() ·
·![]()
令![]() r=3
r=3
∴所求系数为(-2)![]() ·
·![]()
三、
20. C
x>0,
[分析解答] 依题意,得到 即0<x<3.
3-x>0,
(1) 当0<x≤1时,∴ ![]() >0,log
>0,log![]() (3-x)<0,
(3-x)<0,
则有log![]() x-log
x-log![]() (3-x)≥1
(3-x)≥1
log![]() x≥log
x≥log![]()
![]() ,x≤
,x≤![]() ,
,
0<x≤1
∴ x ≤ ![]() ,由
得x∈(0,
,由
得x∈(0,![]() ]
]
x≤![]()
(2) 当1<x≤2时,log![]() x<0,log
x<0,log![]() (3-x)≤0,
(3-x)≤0,
则有-log![]() x-log
x-log![]() (3-x)≥1
(3-x)≥1
log![]() x(3-x)≤-1=log
x(3-x)≤-1=log![]() 3
3
3x-x![]() ≥3,即x
≥3,即x![]() -3x+3≤0 解集为ф
-3x+3≤0 解集为ф
(3) 当2<x<3时,log![]() x<0,log
x<0,log![]() (3-x)>0.
(3-x)>0.
则有-log![]() x+log
x+log![]() (3-x)≥1
(3-x)≥1
log![]() (3-x)≥1+log
(3-x)≥1+log![]() x log
x log![]() (3-x)≥log
(3-x)≥log![]()
![]()
3-x≤![]() , x≥
, x≥![]()
2<x<3,
由
得x∈[![]() ,3)
,3)
x≥![]()
∴ 原不等式的解集为 (0,![]() ]或[
]或[![]() ,3)
,3)
21.
[分析解答]
将两式相加,得到(a-1)(sinα+sinβ)+b(cosα+cosβ)=0
![]()
∵α,β∈(0,![]() ),
),![]() <
< ![]() <
< ![]() , 故
, 故![]() ,
,
∴![]() , ∴
, ∴ ![]()
∵![]() , ∴ a
, ∴ a![]() -1=-b ∴ a
-1=-b ∴ a![]() =1-b
=1-b
22.(1) B (2) D
[分析解答]
| 如图,∵A1B1∥AB,∵ A1B1⊥B1C1 且A1B1⊥A1C,∴ AB⊥B1C1且AB⊥A1C,
∵B1C1∥BC,∴ AB⊥BC.∵A1C∩BC=C, ∴AB⊥平面A1BC连结A1B, ∵A1B在平面A1BC内,∴AB⊥A1B, ∴∠A1BC是二面角A1-AB-C的平面角, |
∴∠A1BC=60°,在Rt△ABC中,
∵AB=3cm, AC=5cm,∠ABC=90°, ∴BC=4cm。在Rt△AA1B中,
∵AB=3cm,AA1=5cm,∠A1BA=90°,∴ A1B=4cm。在△A1BC中
∵∠A1BC=60°,A1B=BC=4cm, ∴ A1C=4cm.
∵AB⊥平面A1BC,AB属于平面ABC, ∴平面ABC⊥平面A1BC,交线为直线BC。
过A1作A1D⊥BC,则A1D⊥平面ABC,
∵△A1BC是边长为4cm的等边三角形,
∴D是BC的中点,且A1D=![]() , A1D是三棱锥A1-ABC的高。
, A1D是三棱锥A1-ABC的高。
∴V![]() 1
1![]() =
= ![]() ·AD1·S
·AD1·S![]() =
= ![]() ·
·![]() ·
·![]() ·3·4
·3·4 ![]()
过D作DE垂直AC,连结A1E,则DE是A1E在底面ABC上的射影,∵AC⊥DE,
∴AC⊥A1E. ∴∠A1ED是二面角A1-AC-B的平面角。∵sin∠ACB=![]() .
.
∴DE=CD·sin∠ACB=![]() . 在Rt△A1DE中,
. 在Rt△A1DE中,
 ∴ 二面角A1-AC-B等于arctg
∴ 二面角A1-AC-B等于arctg![]()
23. [分析解答]
设桶高为h,底面半径为r,成本为y,则有y=3πr![]() +4πrh(元)
+4πrh(元)
∵ ![]() 且V=πr
且V=πr![]() h,∴
h,∴![]()
于是得 y=3πr![]() +4πr·
+4πr·![]()
![]()
![]()
![]()
当3πr![]() =
=![]() ,即
,即![]() 时,等号成立。
时,等号成立。
即当![]() m时,桶的最低成本为
m时,桶的最低成本为![]() 元。
元。
24.
[分析解答]
|
如图,设直线l1:y=k(x+1) 依题意,得到 y=k(x+1) k≠0 => ky y |
∴-1<k<0或0<k<1.
设P的坐标为(xO,yO)
![]() .
.
则有
∴ ![]() ,
,
![]() ,
,
∵ F(1,0), ∴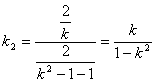 ∴
∴ 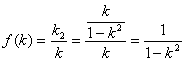
∴ f(k)的定义域为(-1,0)∪(0,1)
∵ -1 < k1 < k2 < 0 => 1 > -k1 > -k2 > 0,
=> 1 >
![]() >
> ![]() > 0 => -1 <
> 0 => -1 < ![]() <
< ![]() < 0,
< 0,
=> 0 < 1-![]() < 1-
< 1-![]() < 1
< 1
=> ![]() >
> ![]() 即f(k1) > f(k2)
即f(k1) > f(k2)
∴k∈(-1,0)时,f(k)是减函数,(-1,0)是递减区间,
同理可证, k∈(0,1)时,f(k)递增,(0,1)是递增区间。
25.(1) D [分析解答]
∵ ![]()
∴ ![]()
(2) A [分析解答]
∵![]() , ∵a1=48. ∴使q
, ∵a1=48. ∴使q![]() 为实数的自然数n最小值为6。
为实数的自然数n最小值为6。
∴数列a1,a2,…,an,…是首项为48,公比为q![]() 的等比数列。 则有a3=a1(q
的等比数列。 则有a3=a1(q![]() )
)![]() =48q
=48q![]()
∵![]()
∴ ![]()
(3) C [分析解答]
∵数列{an}的公比q![]() =
=![]() ∴这个数列的所有项和为
∴这个数列的所有项和为
 .
.