模拟试卷24
一、填空题:
![]()
2.将1、2、3、4、5、6、8、9这八个数组成两个四位数,使这两个数的差最小,这个差是______.
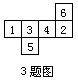
3.如图,将它折成一个正方体,相交于同一顶点的三个面上的数之和最大是______.
4.将1至9这九个数分别填在下面九个方框中,使等式成立:
![]()
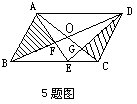
5.如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是______.
6.200个连续自然数的和是32300,取出其中所有的第偶数个数(第2个,第4个,……,第200个),将它们相加,则和是______.
7.某人从甲地到乙地,如果每分钟走75米,迟到8分,如果每分钟走80米,迟到6分,他应以每分钟走______米的速度走才能准时到达.
8.快慢两列火车的长分别是200米、300米,它们相向而行.坐在慢车上的人见快车通过此人窗口的时间是8秒,则坐在快车上的人见慢车通过此人窗口所用的时间是______秒.
9.至少有一个数字是0,且能被4整除的四位数有______个.
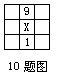
10.如图,九个小正方形内各有一个一位数,并且每行、每列及两条对角线上的三个整数的和相等,那么x=______.
二、解答题:

2.甲、乙、丙三人,甲每五天去李老师家,乙每四天去李老师家,丙每六天去李老师家。三人在1997年元旦去了李老师家,下一次三人在李老师家相聚是几月几日?
3.编号为1至7的7个盘子,每盘都放有玻璃球,共放有80个,其中第1号盘里放有18个,并且编号相邻的三个盘里的玻璃球数的和相等,问第6个盘中玻璃球最多可能是多少个?

已知他骑车每小时行8千米,乘车每小时行16千米,则此人从家到单位的距离是多少千米?
模拟试卷 24
一、填空题:
2.137
要使差最小,被减数与减数应该尽量接近.被减数的千位与减数千位的差是1,它们的末三位数,被减数应该最小,是123,减数应该最大,是986,这样得到被减数是5123,减数是4986,差等于137.
3.相交于同一顶点三个面上的数之和是13.
6+3+4=13
4.73
把4234分解质因数,然后进行计算和调整,有:4234=2×29×73=58×73=29×146
所以最大的两位数是73.
5.1∶3
因为O是AC、BD的中点,所以
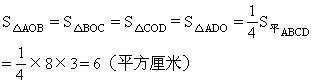
S△AEF+S△BGE=S△AOB-S四边形EFOG
=6-2=4(平方厘米)
S阴影=S平ABCD-(S△AEF+S△BGE)
=12-4=8(平方厘米)
S阴影∶S平ABCD=8∶24=1∶3
6.16200
连续自然数相邻两数之差是1,所以第2个数比第1个数大1,第4个数比第3个数大1,…,第200个数比第199个数大1,100个取出的数比没取出的100个数总共多100,因此所有的第偶数个数之和是
(32300+100)÷2=16200
7.100
设从甲地出发准时到达乙地需x分,则
75×(x+8)=80×(x+6)
80x-75x=600-480
x=24
甲、乙两地距离是:80×(24+6)=2400(米)
从甲地准时到达乙地这人的速度是每分走:
2400÷24=100(米)
8.坐在慢车上的人见快车通过此人窗口时,两列火车共行了200米,用了8秒,得到两列火车的速度和是200÷8=(25米/秒),坐在快车上的人见慢车通过此人窗口时,两列火车共行了300米,所用时间是:300÷25=12(秒).
9.792个
一个数能被4整除的特征是末两位数能被4整除.末两位数应是00、04、08、12、16、20、…、92、96,共25个,其中含有数字0的有7个(00、 04、 08、 20、 40、 60、 80),其余 18个末两位都不含有数字0.
一个四位数的末两位含有数字0,那么它的千位可以是1至9的任意一个,百位是0至9的任意一个,这个四位数的前两位数字共9×10=90个,则末两位含有数字0且能被4整除的四位数共有:
90×7=630(个)
如果末两位不含有数字0,那么要求四位数的百位是0,千位是1至9的任意一个,共有9个,则末两位不含数字0,前两位含有数字0,且能被4整除的四位数共有:
9×18=162(个)
所以至少有一个数字0,且能被4整除的四位数有 630+162=792(个).
10. x=5
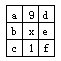
如图所示,a+x+f=9+x+1,有a+f=10;同理d+x+c=9+x+1得d+c=10;
所以 a+f+d+c=20
又 a+9+d=9+x+1,得a+d=x+1;
c+1+f=9+x+1,得c+f==x+9,
则 a+d+c+f=2x+10.
所以 2x+10=20,x=5.
二、解答题:
1.厂里现有工人120名

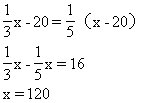
所以厂里现有工人120名.
2.3月1日
[5,4,6]=60,60-(31+28)=1
所以下一次三人在李老师家相聚是3月1日.
3. 第6个盘中的玻璃球最多是12个.

由于相邻三个盘中的玻璃球相等,有编号为1、4、7的盘中玻璃球均相等,等于18个,于是2、3盘中的玻璃球数的和与5、6盘中的玻璃球数的和相等,所以5、6盘中玻璃球数之和是:
(80-18×3)÷2=13(个)
要使第6盘中的玻璃球数最多,第5盘至少是1个(每盘都有玻璃球),所以第6盘最多可能是12个.4.此人家到单位的距离是78千米.设此人家到单位的距离是s千米,他从单位回家用了t小时,则
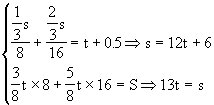
13t=12t+6
t=6
S=13×6=78(千米)
所以此人家到单位的距离是78千米.
模拟试卷 24
一、填空题:
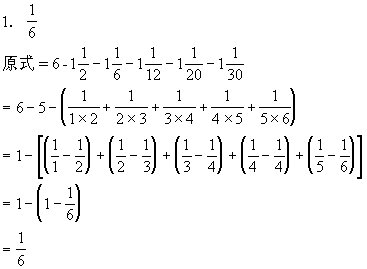
2.137
要使差最小,被减数与减数应该尽量接近.被减数的千位与减数千位的差是1,它们的末三位数,被减数应该最小,是123,减数应该最大,是986,这样得到被减数是5123,减数是4986,差等于137.
3.相交于同一顶点三个面上的数之和是13.
6+3+4=13
4.73
把4234分解质因数,然后进行计算和调整,有:4234=2×29×73=58×73=29×146
所以最大的两位数是73.
5.1∶3
因为O是AC、BD的中点,所以
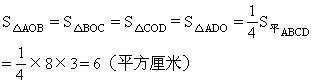
S△AEF+S△BGE=S△AOB-S四边形EFOG
=6-2=4(平方厘米)
S阴影=S平ABCD-(S△AEF+S△BGE)
=12-4=8(平方厘米)
S阴影∶S平ABCD=8∶24=1∶3
6.16200
连续自然数相邻两数之差是1,所以第2个数比第1个数大1,第4个数比第3个数大1,…,第200个数比第199个数大1,100个取出的数比没取出的100个数总共多100,因此所有的第偶数个数之和是
(32300+100)÷2=16200
7.100
设从甲地出发准时到达乙地需x分,则
75×(x+8)=80×(x+6)
80x-75x=600-480
x=24
甲、乙两地距离是:80×(24+6)=2400(米)
从甲地准时到达乙地这人的速度是每分走:
2400÷24=100(米)
8.坐在慢车上的人见快车通过此人窗口时,两列火车共行了200米,用了8秒,得到两列火车的速度和是200÷8=(25米/秒),坐在快车上的人见慢车通过此人窗口时,两列火车共行了300米,所用时间是:300÷25=12(秒).
9.792个
一个数能被4整除的特征是末两位数能被4整除.末两位数应是00、04、08、12、16、20、…、92、96,共25个,其中含有数字0的有7个(00、 04、 08、 20、 40、 60、 80),其余 18个末两位都不含有数字0.
一个四位数的末两位含有数字0,那么它的千位可以是1至9的任意一个,百位是0至9的任意一个,这个四位数的前两位数字共9×10=90个,则末两位含有数字0且能被4整除的四位数共有:
90×7=630(个)
如果末两位不含有数字0,那么要求四位数的百位是0,千位是1至9的任意一个,共有9个,则末两位不含数字0,前两位含有数字0,且能被4整除的四位数共有:
9×18=162(个)
所以至少有一个数字0,且能被4整除的四位数有 630+162=792(个).
10. x=5

如图所示,a+x+f=9+x+1,有a+f=10;同理d+x+c=9+x+1得d+c=10;
所以 a+f+d+c=20
又 a+9+d=9+x+1,得a+d=x+1;
c+1+f=9+x+1,得c+f==x+9,
则 a+d+c+f=2x+10.
所以 2x+10=20,x=5.
二、解答题:
1.厂里现有工人120名

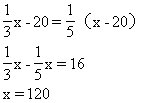
所以厂里现有工人120名.
2.3月1日
[5,4,6]=60,60-(31+28)=1
所以下一次三人在李老师家相聚是3月1日.
3. 第6个盘中的玻璃球最多是12个.

由于相邻三个盘中的玻璃球相等,有编号为1、4、7的盘中玻璃球均相等,等于18个,于是2、3盘中的玻璃球数的和与5、6盘中的玻璃球数的和相等,所以5、6盘中玻璃球数之和是:
(80-18×3)÷2=13(个)
要使第6盘中的玻璃球数最多,第5盘至少是1个(每盘都有玻璃球),所以第6盘最多可能是12个.4.此人家到单位的距离是78千米.设此人家到单位的距离是s千米,他从单位回家用了t小时,则
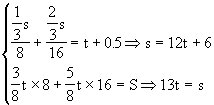
13t=12t+6
t=6
S=13×6=78(千米)
所以此人家到单位的距离是78千米.