模拟试卷26
一、填空题:
1.(4.16×84-2.08×54-0.15×832)÷(0.3)2=______.
2.如果两个自然数相除,商是16,余数是13,被除数、除数、商与余数的和是569,那么被除数是______.
3.某项工作,甲单独干15天可完成.现甲做了6天后另有任务,剩下的工作由乙完成,用了8天.若这项工作全部由乙单独完成需______天.
4.小刚晚上9点整将手表对准,可早晨7点起床时发现手表比标准时间慢了15分,那么小刚的手表每小时慢______分.
5.如图,四边形ABCD的面积是42平方厘米,其中两个小三角形的面积分别是3平方厘米和4平方厘米,那么最大的一个三角形的面积是______平方厘米.
![]()
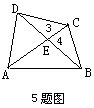
的差最大是______.
7.从1到1000的自然数中,有______个数出现2或4.
8.小红与小丽在一次校运动会上,预测她们年级四个班比赛结果,小红猜测是3班第一名,2班第二名,1班第三名,4班第四名.小丽猜测的名次顺序是2班、4班、3班、1班.结果只有小丽猜到4班是第二名是正确的.这次运动会第一名是______班.
9.将17分成几个自然数的和,再求出这些数的乘积,要使得到的乘积尽可能大,这个乘积是______.
10.小于5且分母为12的最简分数有______个;这些最简分数的和是______.
二、解答题:
1.买6个足球和4个排球共需322元,如果每个足球比每个排球贵7元,每个足球与排球各是多少元?
2.一批苹果装箱.如果已装了42箱,剩下的苹果是这批苹果的70%;如果装了85箱,则还剩下1540个苹果.这批苹果共有多少个?
3.某旅游团安排住宿,若有5个房间,每间住4人,其余的3人住一间,则剩5人;若有2个房间,每间住4人,其余的5人住一间,则正好分完.求有多少个房间?旅游团有多少人?
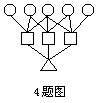
4.如图,将1.8,5.6,4.7,2.8,6.9分别填在五个○内,再在每个□中填上和它相连的三个○中的数的平均值,再把三个□中的数的平均值填在△中.找出一种填法,使三角内的数尽可能大,那么△中填的数是多少?
模拟试卷 26
一、填空题:
1.1248
原式=4.16×(84-4.16×27
-15×2×4.16)÷0.09
=4.16×(84-27-30)÷0.09
=4.16×27÷0.09
=4.16×300
=1248
2.509
设被除数是a,除数是b,则
a=16b+13
a+b+16+13=569
有16b+13+b+16+13=569
17b=527
b=31
所以被除数是
a=16×31+13=509
3.20

![]()
![]()
设手表1小时时针转动一格为路程单位.小刚手表从晚9点到第二天早7点共转了10个格,标准时间应走时间为:
![]()
所以小刚手表的时针每小时转动:

5.20
因为△DEC和△CEB等高,所以
DE∶EB=S△DEC∶S△CEB=3∶4
同理,△ADE与△EAB等高,所以
S△ADE∶S△EAB=DE∶EB=3∶4
又 S△ADB=42-3-4=35(平方厘米)
![]()
=20(平方厘米)
6.36


7.488
从1到99含有数字2的数,一是个位数字是2的有2,12,22,32,…,92,共10个,二是十位数字是2的有20,21,22,…,29,共10个;同理1到99含有数字4的数共20个,其中22、24、42、44被重复计算,所以1到99的自然数中共有20×2-4=36个数出现2或4.从100到199、300到399、500到599、600到699、700到799、800到899、900到999情况与1到99完全相同,而从200到299这100个数的百位上全是2,从400到499这100个数的百位上全是4,而1000既不含2也不含4,所以1到1000含有数字2或4的自然数个数是:
36×8+100×2=488
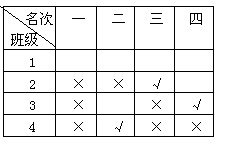
8.1班是第一名
已知4班是第二名,小红猜3班是第一名,小丽猜3班是第三名都不对,所以3班只能是第四名.小红猜2班第二名,小丽猜2班第一名也不对,2班应是第三名(如表),所以1班是第一名.
9.486
将17拆成n个自然数且乘积最大,拆的个数尽可能多,但不要拆成1,且拆成的数不要大于4,例如6拆成3与3比拆成4与2的两数之积要大,因此大于4的数尽可能拆,并且拆成的数2的个数不要超过2个,若多于2个,比如4个2,2+2+2+2=8=3+3+2,显然有3×3×2>2×2×2×2,所以尽可能多拆出3来,这样有
17=3+3+3+3+3+2
所以这个乘积是 3×3×3×3×3×2=486
10.最简分数是20个,和为50.
![]()
其中n=0,1, 2, 3, 4; r=1,5,7,11;且(12,r)=1.所以小于5且分母是12的最简分数共有5×4=20个
这些最简分数的和是
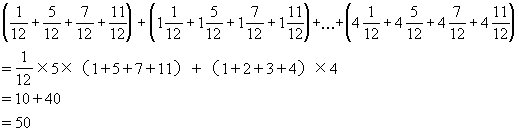
二、解答题:
1.每个足球35元,每个排球28元.
由于每个足球比每个排球贵7元,6个足球比 6个排球贵 7×6=42元,用总钱数 322元减去42元,相当于6+4=10个排球的价钱,得到每个排球的价钱是:
(322-7×6)÷(6+4)=28(元)每个足球的价钱是:
28+7=35(元)
2.这批苹果共3920个
已装箱的42箱苹果相当于这批苹果的1-70%=30%,所以这批苹果共装箱数:
42÷(1-70%)=140(箱)
剩下的1540个苹果恰好装满140-85=55箱,所以每箱苹果个数是
1540÷(140-85)=28(个)
这批苹果的总数是
28×140=3920(个)
3.房间6间,旅游团有28人
“有5个房间,每间住4人,其余的3人住一间,则剩5人”转化成“每间住3人,还剩5+(4-3)×5=10人”;“有2个房间,每间住4人,其余的5人住一间,则正好分完”转化成“每间住5人,还差(5-4)×2=2人”.对比这两个条件知,每个房间相差5-3=2人,几个房间才能相差10+2=12人,可以求出房间数:
[5+(4-3)×5+(5-4)×2]÷(5-3)
=12÷2
=6(间)
旅游团的人数是
4×2+5×(6-2)=28(人)
或4×5+3×(6-5)+5=28(人)
4.△中填5.1
要使三角中的数尽可能大,就要使三个方框中的三个数的和尽可能大.为了便于说明,不妨设五个○中的数依次为 a、 b、 c、 d、 e,三个□中的数依次为x、y、z,△中的数为A.则有
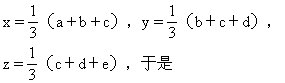
3x=a+b+c,3y=b+c+d,3z=c+d+e三个□里的数的 3倍之和,中间○中c算了 3次,两端○中的a、e各算1次,其余两个数各算2次,应将最大数放在中间○内,把最小和次小的数填在两端○内,剩下的两个数放在剩下的○内.所以3x+3y+3z=6.9×3+5.6×2+4.7×2+1.8+2.8
=45.9
x+y+z=45.9÷3=15.3
A=(x+y+z)÷3=15.3÷3=5.1