模拟试卷27
一、填空题:
![]()

3.将1个棱长是5厘米的正方体分割成若干个小的正方体,这些小正方体的棱长必须是整厘米数.如果这些小正方体的体积不要求都相等,那么最少可以分割成______个小正方体.
4.A、B两数都只含有质因数3和4,它们的最大公约数是36.已知A有12个约数,B有8个约数,那么A+B=______.
5.正方形的一组对边增加6厘米,另一组对边减少4厘米,结果得到的长方形与原正方形面积相等,原正方形的面积是______平方厘米.
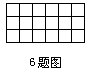
6如图,图中有18个小方格,要把3枚硬币放在方格里,使每行、每列只出现一枚硬币,共有______种放法.
![]()
个数是______.
8.1997名同学排成一排,从排头到排尾1至4报数;再从排尾向排头1至5报数,那么两次报数都报3的共有______人.
9.把一个大长方体木块表面涂满红色后,分割成若干个同样大小的小长方体,其中只有两个面涂上红色的小正方体恰好是16块,那么至少要把这个大长方形分割成______个小长方体.
10.有一个长方形,长有420个小方格,宽有240个小方格.如果把每个小方格的顶点称为格点,连结这个长方形的对角线共经过______个格点(包括对角线两端).
二、解答题:
1.某沿海地区甲、乙两码头,已知一艘船从甲到乙每天航行300千米,从乙到甲每天航行360千米,如果这艘船在甲、乙两码头间往返航行4次共22天,那么甲、乙两码头间的距离是多少千米?
2.有8盏灯,从1到8编号,开始时3、6、7编号的灯是亮的。如果一个小朋友按从1到8,再从1到8,…的顺序拉开关,一共拉动500次,问此时哪几个编号的灯是亮的?
3.一容器内装有10升纯酒精,倒出1升后,用水加满,再倒出1升,再用水加满,然后再倒出1升,用水加满,这时容器内的酒精溶液浓度是多少?
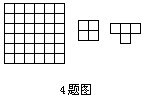
4.能否用2个田字形和7个T字形(如图),恰好覆盖住一个6×6的正方形网格?
模拟试卷 27
一、填空题:
1.85
![]()
=12.5×(1.86+2.54)+30
=12.5×4.4+30
=55+30
=85
2.7
设原来有圆珠笔x支,
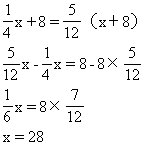
![]()
3.50
要想分割的小正方体个数最少,就要使分割的小正方体的棱长尽可能大.如果小正方体的棱长是4厘米,只能分割出1个,剩下部分的体积是53-43=61立方厘米,只能分割成棱长为1厘米的小正方体,共61÷13=61个,按这种方法分割分成62个小正方体.若在已知正方体的一角分割一个棱长是3厘米的小正方体,剩下7个角可以分割出7个棱长为2厘米的小正方体,这时剩下部分的体积是
53-33-7×23=42(立方厘米)
这部分可以分割棱长是1厘米的小正方体42个,所以总共分割出小正方体个数是:
1+7+42=50(个)
比较上面两种方案,最少可以分割成50个小正方体.
4.684
36=32×4,A、B至少含有两个3和一个4.因为A有12个约数,12=2×6=3×4,所以A可能是35×4、32×43或33×42,B有8个约数,8=2×4,所以B=33×4,于是A只能是32×43,故
A+B=32×43+33×4=684
5. 144
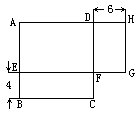
设原正方形的边长为x厘米,如图,由于正方形ABCD与长方形AEGH面积相等,而长方形AEFD是正方形ABCD和长方形AEGH的
公共部分,所以长方形EBCF的面积等于长方形DFGH的面积,于是
4x=6×(x-4)
6x-4x=24
x=12
故原正方形的面积是:
12×12=144(平方厘米).
6.720
第一枚硬币有18种放法;第二枚硬币只能有10种放法,因为这枚硬币放置时与第一枚不同行不同列;同理,第三枚硬币与前二枚硬币不同行也不同列,所以有4种放法.因此共有
18×10×4=720(种)
![]()
这串数的规律是,从第2个数起,每一个数的分子是它前一个数的分子与分母之和,分母是它前一个数的分子的2倍再加分母.若设
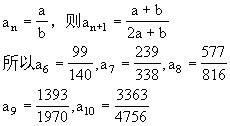
8.100
因为 1997÷4=499…1,所以排尾同学报1,而1997÷5=399…2,所以排头同学报2.

从右起第3名同学两次报数都是3,以后每
相差[4,5]=20名同学两次报数都是3,那么将
1997-3=1994人分成每20人一组,共可分成
1994÷20=99…14
99组,所以两次都报3的人数是99+1=100人.
9.24
由于只有两个面涂上红色的小长方体只能位于每条棱的中间部分,将长方体按下图进行分割:
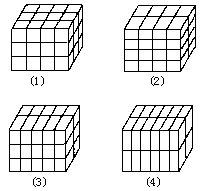
依次分割的小长方体的个数是36、32、30、24,则图(4)分割的块数最少是24块,且恰好有16个两面涂红色的小长方体.
10.61
把长方形按比例缩小,由于
420∶240=7∶4
![]()
所以把长方形缩小成长7个小方格,宽4个小方格的小长方形,然后画一条对角线,如图,图中对角线经过2个格点,即对角线对长来讲,每经过7个小方格,就经过一个格点,或对宽来讲,每经过4个小方格,就经过一个格点,所以长方形的对角线经过的格点问题类似植树问题,共经过格点数:
420÷7+1=61(个)(或240÷4+1=61(个))
二、解答题:
1.甲、乙两码头间的距离是900千米.
由于往返的路程相等,船从甲到乙每天航行300千米,从乙到甲每行航![]()
知往返共22天,可得出从甲到乙行12天,从乙到甲用10天,而300×12+360×10相当于船在甲、乙两码头间往返4次所行的总路程,所以甲、乙两码头的距离.
(300×12+360×10)÷4÷2=900(千米)
2.编号是1、2、4、6、7的灯是亮的.
对于亮着的灯,只要拉动偶数次开关仍是亮的,拉动奇数次开关是灭的;对于开始关闭的灯,只要拉动奇数次开关灯就亮,拉动偶数次开关仍是灭的.因为
500÷8=62…4
说明这8盏灯各拉动62次后,编号为1、2、3、4的灯又拉动一次,由于62是偶数,所以原来亮的灯仍是亮的,灭的灯仍是灭的,即编号是3、6、7的灯各拉动62次后仍是亮的,其余灯是灭的,接着编号是1、2、3、4的灯各拉动一次,编号1、2、4的灯亮了,编号3的灯灭了,所以这8盏灯最后是1、2、4、6、7这五盏灯是亮的.3.容器内的酒精溶液浓度是72.9%第一次倒出纯酒精是1升,加上1升水后,变成酒精溶液,第二次倒出的溶液含纯酒精是:
![]()
第三次倒出的溶液含纯酒精是:
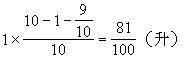
三次倒出后,容器里还有纯酒精是:
![]()
这时容器内溶液的浓度是:
![]()
4.不能
将6×6的正方形网格进行黑白相间染色,黑白格各有18个.每个T字形盖住1个或3个白格,现有7个T字形,若盖住白格数为1的T字形有奇数个,那么盖住白格数为3的T字形是偶数个,奇数个1的和是奇数,偶数个3的和是偶数,所以7个T字形盖住的白格总数,由于奇+偶=奇,因此是奇数个;同理,若盖住白格数为1的T字形有偶数个,那么盖住白格数为3的T字形是奇数个,同样7个T字形盖住的白格总数是奇数个;而2个田字形盖住的白格总数是4,4是偶数,因此2个田字形和7个T字形覆盖的白格总数是奇数个,但6×6的正方形网格的白格数是18个,18是偶数,
由于奇数≠偶数,所以用2个田字形和7个T字形不能覆盖6×6的正方形
网格.