小学数学奥林匹克竞赛模拟题第一部分一节
习题一
1、求所有3位偶数相加的和。
2、求所有被4除余2的两位数的和。
3、求从120到500的所有整数中被6除余5的那些整数的和。
4、下图是一个数字方阵,它有一百行,每一行中有一百个连续自然数,求这个数字方阵中全部自然数的和。
1,2,3,…,98,99,100;
2,3,4,…,99,100,101;
3,4,5,…,100,101,102;
……;
99,100,101,…,196,197,198;
100,101,102,…,197,198,199。
5、若干个同样的盒子排成一排,小明把80多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了。小光从每个有棋子的盒子里各拿3个棋子放在空盒内,再把盒子重新排了一下。小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子。问共有多少个盒子?原来这些棋子是怎样摆放的?
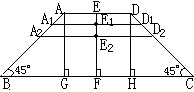
6、给出等腰梯形ABCD(见图1.5),上底长1米,下底长3米,∠ABC=∠DCB=45°。作高EF,从E点沿着高向下,每隔2厘米取一点,过每个分点作与两底平行的直线与两腰相交,这样得到若干条线段,求所有这些平行线的长度总和(不包括上、下底)。
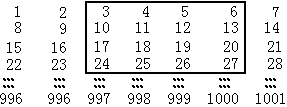
7、将1至1001各数如图1.6的方式排成一个长方形阵列,用一个正方形框出16个数,要使这个方框中的16个数之和等于(1)1968,(2)1988,(3)1991,(4)2000,这是否可能?若不可能,试说明理由;若可以办到,请写出该方框的16个数中最小及最大的数来。
8、老师用若干张纸条,把从1开始的若干个连续奇数依次写在纸条上。写好后捏成纸团,让一个同学从中抽一张出来,然后计算剩下纸条上各数之和,得数为1555,求抽出的那张纸条上写的是哪个数?
9、8个自然数的和为788,其中每两个相邻的数相差都是5,求出这8个数来。
10、给出形如{1,4,10},{3,9,16},{5,14,22},…的由3个自然数组成的数组,求其中第150个数组中那3个数的和。
11、有11个连续奇数,它们的和等于1991,求其中最小的那个数。
12、计算22-32+42-52+62-72+……+1002-1012+1022,这里记号a2定义为a×a,例如:42=4×4=16,注意42≠4×2。
13、给定数列2,8,14,20,…,(1)下面哪些数在此数列中?是其中的第几个数?38,6512,13870,835916;(2)求这个数列中前面100个数的和;(3)计算2+8+14+20+…+4716;(4)已知此数列中前n个数的和是352,求n的值。
14、给定一个等差数列,它的第一个数是a1=2,而其中第n个数是an=48。如果已知其中前n个数的和是偶数,且2和48不是两个相邻的数。(1)求n=?(2)下面哪些数在这个数列中?如果在,是其中第几个数?351,716,1734(3)如果已知这个数列中前面m个数的和等于6806,求m=?
习题一提示及部分解答
1、先求出最小及最大的3位偶数,再求出这样的偶数一共有多少个。
2、先求出两位数中被4除余2的最小及最大的数,再求出一共有多少个这样的数。
4、这个题目可有若干种不同的解法:解法一、先按行求和。这时要注意前面每行数的和与紧接在后面那行数的和相差一个固定的数,从而把本书例子的方法使用两次就可以得出结果。解法二、把整个数字方阵沿数字100所在的那条对角线对折,这样就使所有的数两两重合在一起,例如左上角的1与右下角的199重在一起,……。注意每一对相重合的数相加所得结果一样,也可以得出同样结果。
5、按照盒中棋子个数排列这些盒子,根据题目条件判断盒中棋子个数从小到大应是0,3,6,9,…,再根据棋子总数有80多个即可求出棋子最多的盒中有多少个棋子。
6、过梯形顶点A及D再分别作BC边上两条高AG及DH,利用AD=1米及锐角为45°的任何直角三角形的两直角边长相等即可求出第一条平行线长为A1D1=1+0.02×2(米),第二条平行线长为A2D2=A1D1+0.02×2(米),…,于是可按等差数列求和。
7、观察图1.6中方框里的16个数,注意先按行求和,每相邻两行中4个数的和都相差7×4=28,于是,如果用S1表示方框中第一行里4个数的和,证明方框中16个数的和应为
4S1+28+28×2+28×3, (1)
根据(1)式可以决定题目所给的几个数中哪些是不符合题意的。
如果是对某个给出的数(作为某方框中的16个数的和),根据(1)式找到了相应的S1,还要进一步讨论;是否在图1.6中某一行中4个连续自然数之和恰等于S1。例如:若算得有S1=66,由x+(x+1)+(x+2)+(x+3)=66解得x=15,这表示15,16,17,18这4个数的和为66,这4个数在同一行,因而是允许的,若算得有S1=82,由x+(x+1)+(x+2)+(x+3)=82解得x=19,即19,20,21,22这4个数的和等于82,但这4个数并不在同一行(见图1.6),因而是不允许的。
8、先明确第n个奇数可用2n-1来表示,再用本书方法推出前n个奇数和的公式应为
1+3+5+…+(2n-1)=n2, (2)
设抽出的那张纸条上写的数是x,就有
1≤x≤2n-1, (3)
再由题目条件及(2)式有
n2-x=1555。 (4)
由(4)式及x≥1有n2-1≥1555,
因此(注意402=1600)不难得到
n>39 (5)
又由(4)式及x≤2n-1有
n2-(2n-1)≤1555,
试验可得
n≤40。 (6)
由(5)及(6)即得n=40,因而x的值可从(4)式得出。
9、解法一:相差为5的最小的8个自然数是1,6,11,16,21,26,31,36,研究这8个数的和与788相差多少,然后设法改变它们,使得另外找出的8个自然数的和恰为788;解法二:设8个数中最小的数为x,把其余7个数用含字母x的式子表示出来,由题意立方程即可。解法三:先求出中间两个数的和。
10、注意本题中暗含有以下3个等差数列:1,3,5,…;4,9,14,…;10,16,22,…。求出每个数列中第150个数再求和即可。
另解:把每一数组中3个数相加得一新的数列,即为1+4+10=15,3+9+16=28,5+14+22=41,…它仍是一个等差数列,求出这个新数列中第150个数即所求者。
11、参看第9题提示,注意每两个连续奇数相差为2。
12、把所求的式子改写成22+(42-32)+(62-52)+…+(1002-992)+(1022-1012)注意42-32=4+3,62-52=6+5,…,即不难计算了。
13、(1)把数列中的数依次写成以下形式2=2+6×0;8=2+6×1;14=2+6×2;20=2+6×3。(注意数列中相邻两数之差皆为6),研究38等4个数是否能写成这样的形式;(2)先求数列中第100个数是多少(参考(1)中的形式);(3)先算出4710是这个数列中第几个数(参考(1)中形式);(4)设an是这数列中第n个数,用书中例子的方法推出2+8+14+…+an=![]() ,于是由条件有(2+an)n=2×352=704。然后分解704成两个自然数的积,选择其中一个因数作为n,另一个作为2+an,注意当n取定后,an=2+6(n-1)由n所决定。
,于是由条件有(2+an)n=2×352=704。然后分解704成两个自然数的积,选择其中一个因数作为n,另一个作为2+an,注意当n取定后,an=2+6(n-1)由n所决定。
14、(1)注意本题中并没有给出数列中相邻两数的差d是多少,这需要你通过题给条件判断。我们有an-a1=46,注意d必定是46的约数,而46=1×46=2×23,因而d有1,2,23及46这4个可能的值,题目中“前n个数的和为偶数”及“2和48不是两个相邻的数”这两个条件可用来帮助你决定d的值。有了d的值,这个数列就完全确定了,其余几个问题可仿13题求解。