第三章 整式的加减（一）
班级 姓名
1．在式子0，
，
，
，
中，代数式的个数有（ ）
A．5个 B．4个 C．3个 D．2个
2．代数式
的意义是（ ）
A．
与
的平方的差
B．减去的平方的差
C．与的差的平方
D．的平方减的平方
3．若
是整数，则下列代数式中表示奇数是（ ）
A．
B．
C．
D．
4．若甲数是
，甲数是乙数的
，则乙数是（ ）
A．
B．
C．
D．
5．
…
等于（ ）
A．
B．
C．
D．
6．50名学生报名参加A、B两个课外活动小组，有
个人报名参加A组，有个人报
名参加B组，两组都没有报名的有5人，则两组都参加的人数是（ ）
A．
B．
C．
D．
1
7.用代数式表示x与5的差的2倍，正确的是（ ）
A，x－5×2 B，x+5×2 C，2(x－5) D，2(x+5)
8．当
，
时，下列代数式的值最大的是（ ）
A．
B．
C．
D．
9．若、互为相反数，、
互为倒数，则
的值是（ ）
A．2 B．3.5 C．4 D．3
10．规定运算“
”为：
，则
＝（ ）
A．4 B．5 C．6 D．7
11．有理数
的值一定不是（ ）
A．2002 B．－2003 C．0 D．1
12．已知：代数式
的值等于8，则
的值是（ ）
A．2 B．－17 C．－7 D．7
13.一件工作，甲单独做需a天完成，乙单独做需b天完成，如果两人合作7天，完成的工作量是（ ）
A，
B，7(a－b) C，7(a+b) D，
14.已知某商场打7折后的价格为a元，则原价为（ ）
A，
元 B，
元
C，
元 D，
元
15．已知上山的速度为
，下山的速度为
，来回的平均速度为（ ）
A，
B，
C，
D，
16．某班共有x名学生，其中男生人数占
，那么女生人数是（ ）
A，
B，
C，
D，
17. 当x＝3时，代数式px2＋qx＋1的值为2002，则当x＝－3时，代数式
px2＋qx＋1的值为 ( )
A.2000 B.－2002 C.－2000 D.2001
二、填空题
1．若
，
，则
＝ ．
2．当
时，代数式
的值是
．
3．若
，
，
，则
＝ ．
4．已知：
，
，则
＝ ．
5．写出
正确的代数式：
．
6．某商品的定价为元，降价10%后的售价为
元．
7．在小学，我们学过简便运算，如
．用字母表示这个运算规律，得：
．
8．如果昨天的气温是27℃，今天比昨天升高
℃，那么今天的气温是
℃．
9．有一列数1，2，3，4，5，6，…当按顺序从第个数数到第个数（＞）时，共数了
个数．
10．某市出租车收费标准为：起步价6元，3千米后每千米1.2元．则某人乘坐出租车
（＞3）千米的付费为
元．
11．n千克玉米售价为m元，1千克玉米的售价为 元
12．一辆汽车行走的路程为s，所用的时间为t，则它的速度为
13．一个三角形的底边长为a，高为h，则这个三角形的面积为
14．比a与3的和的一半大3的数是
15．由两种本，一种单价是0.3元，另一种单价是0.5元，买这两种本的本数分别是a和b，问供需 元
16．三个连续自然数，中间的一个是n，则其他两个数分别是
三、解答题
1．说出下列代数式的意义
（1）
（2）
（3）
（4）
2．用代数式表示
（1）比a的倒数与b的倒数的和大1的数 （2）被3整除得n的数
（3）被5除商a余3的数 （4）比x与y的积的倒数的4倍小3的数
（5）a,b两数的平方和除以a,b两数的和的平方
3．已知的相反数是
，的倒数是
，求代数式
的值．
4．当时，求代数式
的值．
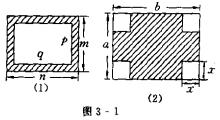
5．如图3-1所示，用代数式表示图中阴影部分的面积
6.将甲乙两种糖果混合后出售，已知甲种糖果每千克m元，取a千克；乙种糖果每千克n元，取b千克，则混合后每千克糖果的售价应是多少元？
7.一根绳长a米，第一次用掉了全长的
多1米，第二次用掉了余下的
少2米，最后还剩多少米？
8.某是为了加强公民的节水意识，制定了以下用水标准：每户每月用水未超过8立方米时，每立方米收费1.00元，并加收0.20元的城市污水处理费；超过8立方米的部分每立方米收费1.50元，并加收0.40元的城市污水处理费。某户用水量为x立方米，问这个月水费是多少元？
9．某汽车厂以每年产量增加9%的速度发展，设2002年汽车的产量是辆，那么
（1）2003年汽车的产量达到多少辆？
（2）2004年汽车的产量达到多少辆？
（3）2008年汽车的产量达到多少辆？
10．观察下列各式：
第1式：1×2×3×4＋1；
第2式：2×3×4×5＋1；
第3式：3×4×5×6＋1；
……
（1）写出第9式；
（2）用代数式表示第式
11．某会议大厅，第排有个座位，与的关系如下表：
| 排数 | 1 | 2 | 3 | 4 | 5 | … |
| 座位数 | 32 | 35 | 38 | 41 | 44 | … |
（1）写出和的关系式
（2）求第10排的座位数
12.你能很快计算出
吗？
为了解决这个问题，我们来考察个位为5的自然数的平方，任意一个个位为5的自然数都可以写成10n+5的形式，于是原题即求
的值。N为自然数，分析n=1,n=2,n=3,……这些简单情况，从中探索其规律，并归纳、猜想出结论。
（1）通过计算、探索规律：
=
=
=
（2）从（1）小题的结果，归纳、猜想得：
=
（3）根据上面的归纳、猜想，请计算出=