典型例题
例1 甲、乙两个工程队共有120人,其中乙队人数比甲队人数的2倍还多6人,求甲、乙两队各有多少人?
分析:设甲队有x人,乙队人数比甲队的2倍还多6人,用代数式表示:
乙队为(2x+6)人,于是有:

等量关系:甲队人数+乙队人数=120
解:设甲队有x人,依题意有
x+(2x+6)=120
x+2x+6=120
3x=114
x=38
乙队人数为:38×2+6=82
答:甲队有38人,乙队有82人.
说明:如果这个题设乙队有x人,则甲队的人数是![]() 人,显然所列代数式比设甲队有x人复杂而且容易出错.所以列方程解应用题时,在认真审题的基础上,第一个关键步骤就是如何“设未知数”.
人,显然所列代数式比设甲队有x人复杂而且容易出错.所以列方程解应用题时,在认真审题的基础上,第一个关键步骤就是如何“设未知数”.
选题角度:关于调配问题,含有关键字“几倍”的题目
例2 一种绘图工具的新价比原价少0.5元,按新价买该种工具19件,比按原价买18件省6元人民币.求这种工具的原价.
分析:这个问题涉及三个基本量——单价、数量、金额,基本数量关系是:单价×数量=金额,关键词是“比”、“省”.
如果设该种工具的原价为x元,依题意有:
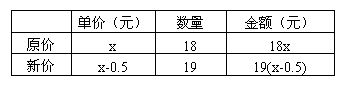
由尚未用上的已知条件——按新价比原价省6元,可得方程.
解:设这种工具的原价为x元,
则这种工具的新价为(x-0.5)元.
19(x-0.5)=18x-6
19x-9.5=18x-6
x=3.5
答:这种工具的原价是3.5元.
说明:这个题的方程也可以列为19(x-0.5)-18x=-6,或19(x-0.5)+6=18x等.
选题角度:关于含有关键字“比”、“省”的应用题;
例3 一个个位数是4的三位数,如果把这个数4换到最左边,所得的数比原数的3倍还多98,试求原数.
解:设这个三位数去掉尾数4,剩下的是二位数为X,那么这个三位数应表示为![]() 。
。
把尾数4换到最左边得到的数应为![]() .依题意得方程
.依题意得方程
![]()
解这个方程,得![]() .
.
原数为104.
答:原数为104.
说明:要想圆满解答本题,必须对十进制数的数位有正确的认识,一个三位数:□□4,设□□=x,即二位数设为x,那么关键点是这个三位数如何表示?——应是![]() .而不应是
.而不应是![]() ,为什么?——这是因为4是三位数的个位,而x表示三位数中的百位、十位合起来的两位数。假设
,为什么?——这是因为4是三位数的个位,而x表示三位数中的百位、十位合起来的两位数。假设![]() .这就不是三位数了!
.这就不是三位数了!
一般来说,解数字问题的关键是要掌握表示位数的方法,如果是三位数,则表示成![]() ,并注意求得的某数最高位数字不能是零,且每个数位上的数字都应该是一位数.
,并注意求得的某数最高位数字不能是零,且每个数位上的数字都应该是一位数.
选题角度:关于数字问题的应用题
例4 一件工程,如果甲工程队单独做完需要56小时,乙工程队单独做完需要80小时,现在甲、乙两个工程队合做需几小时完成?
分析:我们找出题中的两个相等关系:
甲工作时间=乙工作时间 ①
甲的工作量+乙的工作量=1 ②
今想办法表示出甲、乙的工作效率.
由基本数量关系:
![]()
设总工作量为1,于是有
甲的工作效率![]() ,乙的工作效率
,乙的工作效率![]()
如何列出方程呢?——设甲、乙两个工程队合做的时间为x小时,就可以列出甲、乙分别完成的工作量,再由相等关系②就可以列出方程来。
解:设甲、乙两个工程队合做的时间为x小时(这里使用了关系①),在x小时内,甲、乙完成的工作量分别为![]() 。
。
由关系②可得方程:
![]() ,
,
解这个方程,得![]() (小时).
(小时).
答:甲、乙两个工程队合做![]() 小时,可以完成工程。
小时,可以完成工程。
选题角度:关于工程方面的应用题
例5 目前,包括长江、黄河等七大流域在内,全国水土流失面积达到367万平方千米,其中长江与黄河流域的水土流失总面积占全国的32.4%。而长江流域的水土流失问题更为严重,它的水土流失面积比黄河流域的水土流失面积还要多29万平方千米。问长江流域的水土流失面积是多少?(结果保留整数)
(2001年安徽)
分析:应以长江、黄河的水土流失面积来列方程解之。
解:设长江流域水土流失面积为x万平方千米。根据题意,得
![]()
解得 ![]() 。
。
答:长江流域水土流失面积约是74万平方千米。
说明:本题属社会热点问题,应为长江流域有关省份学生关注的问题。而由此题改编后的题目,即针对黄河而言,也应引起黄河流域省份的学生关注。
习题精选
一、选择题
1.某数的2倍加上8,等于这个数的![]() 加上7,这个数是( ).
加上7,这个数是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.一个五位数,它的前三位数是a,后两位数是b,如果把后两位数b放在前三位数a的前面,组成一个新的五位数,则这个五位数为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.一轮船在静水中航行的速度为v,河水的流速为![]() ,顺水速度是逆水速度的两倍,则有(
).
,顺水速度是逆水速度的两倍,则有(
).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.一项工程,甲单独做需a天完成,乙单独做需b天完成,两人合做比甲单独做提前完成的天数为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.甲比乙大15岁,5年前甲的年龄是乙的两倍,乙现在的年龄是( ).
A.10岁 B.15岁 C.20岁 D.30岁
6.某商贩在一次买卖中同时卖出两件上衣,每件都是135元,若按成本计算,其中一件盈利25%,另一件亏本25%,则在这次买卖中他( ).
A.不赚不赔 B.赚9元 C.赔18元 D.赚18元
7.某商场的电视机按原价的9折出售,要使销售的总收入不变,那么销售量需增加( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知甲数的3倍等于乙数的4倍,且甲数比乙数大8。则甲数等于().
A.16 B.24 C.32 D.44
9.甲以5千米/时的速度先出发16分钟,乙以13千米/时的速度追甲,则乙追上甲所用时间为().
A.10小时 B.![]() 小时 C.
小时 C.![]() 小时 D.6小时
小时 D.6小时
10.某商品的价格,前年为![]() 年,去年上涨了10%,今年又下降了10%,则该商品今年的价格与前年的价格相比,结论是().
年,去年上涨了10%,今年又下降了10%,则该商品今年的价格与前年的价格相比,结论是().
A.价格相等 B.今年的价格比前年高
C.今年的价格比前低 D.不确定
11.几个人搬一堆砖,若每人搬![]() 块,还剩14块;若每人搬
块,还剩14块;若每人搬![]() 块,最后一人只搬6块。计算搬砖人数及
块,最后一人只搬6块。计算搬砖人数及![]() 的值可能是().
的值可能是().
A.17人,![]() B.17人,
B.17人,![]()
C.11人,![]() D.11人,
D.11人,![]()
12.甲、乙两人去商店买东西,他们所带的钱数之比为![]() ,甲用去50元,乙用去60元。两人余下的钱数之比为
,甲用去50元,乙用去60元。两人余下的钱数之比为![]() ,则两人原有钱数分别是().
,则两人原有钱数分别是().
A.甲98元,乙84元 B.甲105元,乙90元
C.甲140元,乙120元 D.甲147元,乙98元
13. 某乡1998年粮食人均占有量544千克,比1949年人均占有量的4倍还多32千克。如果设1949年人均占有量为![]() 千克,下面所列方程错误的是().
千克,下面所列方程错误的是().
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14. 一架飞机在A、B两城市间飞行,顺风要![]() 小时,逆风要6小时,风速为24千米/时,求A,B两城市间距离
小时,逆风要6小时,风速为24千米/时,求A,B两城市间距离![]() 的方程是().
的方程是().
A.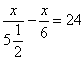 B.
B.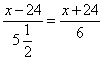
C.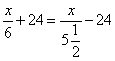 D.
D.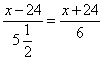
15. 某工程队单独做6小时完成,乙队单独做4小时完成,现两队合作1小时后,再由乙队单独完成,那么完成这个工程共需的小时数是().
A.![]() 小时 B.
小时 B.![]() 小时 C.
小时 C.![]() 小时 D.
小时 D.![]() 小时
小时
二、填空题
1.甲队原有![]() 人,乙队原有
人,乙队原有![]() 人,现从乙队抽调
人,现从乙队抽调![]() 人去甲队,则甲乙两队现有人数分别为_________,_________;
人去甲队,则甲乙两队现有人数分别为_________,_________;
2.乙知一列火车从A地开往B地速度为120公里/小时,火车行驶了![]() 小时则所行路程为_________公里.
小时则所行路程为_________公里.
3.某人以4千米/小时的速度由甲地到乙地,然后又以6千米/小时的速度从乙地返回甲地,那么他往返一次的平均速度是_________.
4.某人完成一项工作,当他的工作时间减少20%时,他的工作效率提高的百分数是__________.
5.某商品售价7.2元,利润为20%,若要将利润提高到25%,则售价提高_______元.
6.学校为节约用水,每月水费按以下规定收取:用水不超过10吨,按每吨0.80元收费;如果超过10吨,超过部分按每吨1.20元收费.王老师三月份的水费平均每吨0.95元,则他三月份用了_______吨水,应交水费________元.
7.某人以八折优惠价买一套衣服节省15元钱,则此人买这套衣服用去________元钱.
8.m个苹果分给n个小朋友,若每人5个,则余1个;若每人6个,则缺3个,则mn=____.
9.从1999年11月1日起,全国储蓄存款需征收利息税,利息税的税率是20%,张老师于1999年5月1日在银行存入人民币2万元,定期一年,年利率为3.78%,存款到期后,张老师净得本息和共计______元.
10.有一六位数![]() ,若将6移到左边为
,若将6移到左边为![]() ,则新数是原数的4倍,则原数为_____.
,则新数是原数的4倍,则原数为_____.
11.若甲数为![]() ,它的2倍比乙数少9,则乙数可表示为__________;
,它的2倍比乙数少9,则乙数可表示为__________;
12.某商品原来的售价为![]() 元,降价8%后的售价为_________元;
元,降价8%后的售价为_________元;
13.一列慢车从甲站开往乙站,速度为56千米/时,同时一列快车从乙站开往甲站,速度为72千米/时,![]() 小时后两车相遇,则甲、乙两站间的距离为_______千米;
小时后两车相遇,则甲、乙两站间的距离为_______千米;
14. 一个矩形的周长是16厘米,长比宽多2厘米,那么长是_______。
15. 某市初一数学竞赛共有20道题,答对一题5分,不答或答错一题不仅不给分,还要扣去3分,要想得到84分必须答对的题数是________。
16. 四年前哥哥的年龄是弟弟年龄的2倍,今年哥哥的年龄是弟弟的![]() 倍,那么哥哥今年的年龄是______。
倍,那么哥哥今年的年龄是______。
三、解答题
1.现有面值为2元和5元的人民币共39张,币值共计111元,问两种人民币各有多少张?
2.小红去商店买了5个练习本和3支铅笔,共花去5元4角,知道一个练习本比一支铅笔贵1角2分.问练习本、铅笔价格各是多少?
3.育红小学现有学生320人,比1995年学生人数的![]() 倍还少150人.问育红小学1995年学生人数是多少?
倍还少150人.问育红小学1995年学生人数是多少?
4.抗洪抢修施工队甲处有31人,乙处有21人,由于任务的需要,现另调23人去支援,使在甲处施工的人数是在乙处施工人数的2倍,问应调往甲、乙两处各多少人?
5.一辆汽车从A地到B地用去油箱里汽油的25%;从B地到C地用去余下汽油的15%,结果油箱里剩下8升汽油.问油箱里原来有汽油多少升?
6.甲乙两地相距460千米.A、B两车分别从甲、乙两地开出,A车每小时行驶60千米,B车每小时行驶48千米.
(l)两车同时开出,相向而行,出发后多少小时两车相遇?
(2)两车相向而行,A车提前半小时出发;B车开出后多少小时两车相遇?相遇地点距离甲地多远?
(3)两车同向同时开出,B车在前,出发后多少小时A车追上B车?
(4)两车背向而行,同时出发,行驶多少小时两车相距960千米?
(5)两车相向而行,同时出发,相遇后两车继续前进,当A车到达乙地时,B车距甲地多远?
7.甲、乙二人从A城去B城,甲步行每小时走4千米,乙骑车每小时比甲多走8千米.甲出发半小时后乙出发,恰好H人同时到达B城,求A、B两城之间的距离.
8.一架飞机在两个城市之间飞行,无风时飞机每小时飞行552干米,在一次往返飞行中,飞机顺风飞行用去![]() 小时,逆风飞行用了6小时.求这次飞行的风速?
小时,逆风飞行用了6小时.求这次飞行的风速?
9.A、B两地相距496千米,甲车以每小时32千米的速度从A开往B,半小时后,乙车从B开往A,速度是甲的2倍,问乙车开出几小时后两车相遇?
10.某工作,甲单独做需用15小时完成,乙单独做需要12小时完成,若甲先独做1小时,乙又单独做4小时,剩下的部分两人合做,再用几小时可以完成?
11.一车间原有80人,二车间原有372人,今由于工作需要,除要从三车间调4人到一车间外,还需从二车间调多少人去一车间,才能使一车间人数是二车间人数的一半?
12. 甲、乙二人编织一种工艺品,甲每5分钟编一件,乙每6分钟编一件,在同一时间内两人共编121件。求(1)甲、乙二人在这一时间内各编了多少件;(2)用的时间是多少?
13.某商店将彩电按原价提高40%,然后在广告中写上“大酬宾,八折优惠”,结果每台彩电比原价多赚270元,那么每台彩电原价多少元?
14.一个四位数,左边第一位数字是7,若把这个数字调到末尾,得到的新数比原四位数少864,求原四位数.
15.一队战士用4千米/时的速度行军,在队尾的通讯员以6千米/时的速度跑至队首传令给队长,然后立即按原速返回队尾,共7.2分钟,求这列队伍的队长.
16.某种商品的进价降低6.4%后,售出价不变,则商品的利润率由原来的m%增加到![]() ,求m.(△)
,求m.(△)
17.从甲地到乙地,先下山后走平路,某人骑自行车从甲地以每小时12千米速度下山,又以每小时9千米速度通过平路,到乙地用了55分钟,他回来时以每小时8千米的速度通过平路,又以每小时4千米的速度上山,回到甲地用1.5小时,求甲乙两地的距离.(△)
18.一个三位数,三个数位上的数字之和为17。百位上的数比十位上的数大7,个位上的数是十位上的数的3倍,求这个三位数。
19.一个三位数,个位数字是5,如果把5放到这个三位数的百位数上。原来百位上的数字移至十位,原来十位上的数字移至个位,那么得到的新数则比原数的3倍小95。求原三位数。
20.一艘轮船航行于甲、乙两码头之间,顺流需3小时,逆流需![]() 小时,已知船在静水中的速度为26千米/时,求水流速度。
小时,已知船在静水中的速度为26千米/时,求水流速度。
21.某商品月末的进货价比月初的进货价下降了8%,而销售价不变。这样,利润率月末比月初高出10%,问月初的利润率是多少?
22.有两种合金,第一种含铜90%,第二含铜80%,现要熔炼一种含铜![]() 的合金240千克。两种合金应各取多少千克?
的合金240千克。两种合金应各取多少千克?
研究题:
某深长做作业时,不慎将墨水瓶打翻,使一道作业题只能看到如下字样:“甲、乙两地相距40千米,摩托车的速度为45千米/时,货车的速度为35千米/时,……”(省略号部分是被墨水覆盖住的若干文字)。请你把这道作业题补充完整,并列方程解答。
答案:
一、1.B 2.D 3.C 4.C 5.C 6.C 7.C. 8.C 9.B 10.C 11.A 12.C. 13. A; 14. C;15. B.
二、1.![]() ,
, ![]() 2.
2. ![]() ; 3.4.8千米/小时 4.25% 5.0.3 6.16;15.2 7.60 8.84 9.20680.4 10.153846 . 11.
; 3.4.8千米/小时 4.25% 5.0.3 6.16;15.2 7.60 8.84 9.20680.4 10.153846 . 11.![]() ;12.
;12.![]() ;13.
;13.![]() ;14. 5厘米;15. 18 ; 16. 12.
;14. 5厘米;15. 18 ; 16. 12.
三、1.2元的28张,5元的11张.提示:设5元的有![]() 张,则2元的有(39-
张,则2元的有(39-![]() )张.根据题意得:
)张.根据题意得: ![]()
2.7角2分;6角.设铅笔每支![]() 元,则练习本每本
元,则练习本每本![]() 元,根据题意得:
元,根据题意得:![]() .
.
3.705人,设育红小学1995年学生人数为![]() 人,根据题意得:
人,根据题意得:![]()
4.19人,4人.设应调往甲处![]() 人,则应调往乙处
人,则应调往乙处![]() 人,根据题意得:
人,根据题意得:![]() .
.
5.![]() 升.设原来油箱中有油为
升.设原来油箱中有油为![]() 升,根据题意得:
升,根据题意得:![]()
6.(1)![]() 小时;(2)
小时;(2)![]() 小时;
小时;![]() 千米;(3)
千米;(3)![]() 小时,(4)
小时,(4)![]() 小时;(5)92千米
小时;(5)92千米
(1)设出发后![]() 小时相遇,根据题意得:
小时相遇,根据题意得:
![]()
(2)设B车开出后![]() 小时两车相遇,根据题意得:
小时两车相遇,根据题意得:
![]()
(3)设出发后![]() 小时A车追上B车,根据题意得:
小时A车追上B车,根据题意得:
![]()
(4)设行驶![]() 小时两车相距960千米,根据题意得:
小时两车相距960千米,根据题意得:
![]()
(5)设B车距甲地![]() 千米,根据题意得:
千米,根据题意得:
![]()
7.3千米.设A、B两城之间的距离为![]() 千米,根据题意得:
千米,根据题意得:
![]()
8.24千米/小时.设这次飞行的风速为![]() 千米/小时,根据题意得:
千米/小时,根据题意得:
![]()
9.设乙车开出x小时后两车相遇,根据意得![]() ,解之得
,解之得![]() ,故乙车开出5小时后两车相遇
,故乙车开出5小时后两车相遇
10.设再用x小时可以完成,工作总量为1,根据题意
![]() ,解之得
,解之得![]() ,故再用4小时可以完成.
,故再用4小时可以完成.
11. 68人。
12. (1)甲66件,乙55件 (2)5![]() 小时。
小时。
13.设每台彩电原价为x元,根据题意,得![]() ,解之得
,解之得![]() ,故每台彩电原价为2250元
,故每台彩电原价为2250元
14.设这个四位数为x,根据题意得![]() ,解之得
,解之得![]() =7681。
=7681。
15.设这列队伍长x千米,根据题意得![]() ,解之得
,解之得![]() ,故这列队伍长200米 。
,故这列队伍长200米 。
16.设原进货为1,则后来的进货价为![]() ,根据题意得
,根据题意得
![]() 解之得
解之得![]()
17.设甲、乙两地坡路x千米,根据题意得![]() ,解之得
,解之得![]() ,甲、乙两地平路
,甲、乙两地平路![]() (千米),故甲、乙两地相距9千米.
(千米),故甲、乙两地相距9千米.
18.926;
19.205
20.2千米/时;
21.15%
22.第一种合金取60千克,第一种合金取180千克。
研究题:
提供3种补充:
(1)若两车同时从甲、乙两地出发、相向而行。经过几小时两车相遇?(答:![]() 小时)
小时)
(2)若摩托车先出发12分钟,相向而行,问货车出发几小时两车相遇?(答:![]() 小时)
小时)
(3)若两车同时从甲、乙两地出发,同向而行。货车在摩托车前,经过几小时摩托车可追上货车?(答:4小时)