初一数学下能力测试题（四）
班级 姓名
一、填空题
1、
，
2、
；
3、
；
4、300角的余角是__________0，补角是___________0
5、已知一个角的余角是它的补角四分之一，则这个角的度数是__________0
6、
；
7、如果(2x+3)(ax—5)=2x2—bx+c，则a=________;b=________;c=_________
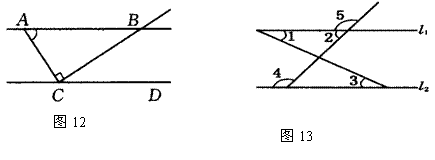
8、如图，若∠2=∠3，则根据 ，
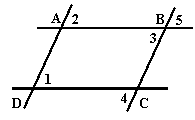可得
；
若∠2=∠1，则根据 ，
可得 ；
如果AD∥BC，那么根据 ，
可得 ；(只填图中标出的角)
如果AB∥CD，那么根据 ，
可得 。(只填图中标出的角)
9、如图，如果∠1=∠2，则互相平行的线段是____________.
 | |||
 | |||
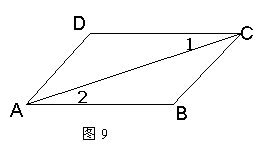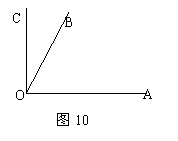10、如图：已知∠AOB=2∠BOC，且OA⊥OC，则∠AOB=_________0
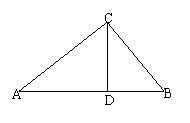11、如图：∠ACB=900，CD⊥AB，
则图有互余的角有_________组
若∠A=
∠B，则∠ACD=__________0
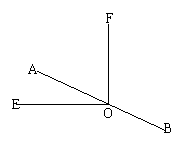12、如图所示：已知OE⊥OF
直线AB经过点O，则∠BOF—∠AOE=__________
若∠AOF=2∠AOE，则∠BOF=___________
二、选择题
1、下列计算中，运算正确的有几个（ ）
(1) a5+a5=a10 (2) (a+b)3=a3+b3 (3) (—a+b)(—a—b)=a2—b2 (4) (a—b)3= —(b—a)3
A、0个 B、1个 C、2个 D、3个
2、下列各式的计算中，正确的是（ ）
A、(a5÷a3)÷a2=1 B、(—2a2)3= —6a6 C、—(—a2)4=a8 D、(a2)3=a5
3、计算
的结果是（ ）
A、—2 B、2 C、4 D、—4
4、已知(a+b)2=m，(a—b)2=n，则ab等于（ ）
A、
B、
C、
D、
5、下列各式中，计算错误的是（ ）
A、(x+1)(x+2)=x2+3x+2 B、(x—2)(x+3)=x2+x—6
C、(x+4)(x—2)=x2+2x—8 D、(x+y—1)(x+y—2)=(x+y)2—3(x+y)—2
6、在同一平面内，如有三条直线a、b、c满足a∥b，b⊥c，那么a与c的位置关系是（ ）
A、垂直 B、平行 C、相交但不垂直 D、不能确定
7、下列各式中能用平方差公式计算的是（ ）
A、(—3x+2y)(3x—2y) B、(—a—3b+c)(a+3b—c)
C、(3x—5y—2)(—3x+5y—2) D、(a+b+3)(a+b—2)
8、若一个角的两边与另一个面的两边分别平行，则这两个角（ ）
A、相等 B、互补 C、相等且互补 D、相等或互补
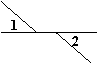
9、在下图中，∠1和∠2是对顶角的图形是 ( )
 | |||||||
 | |||||||
 | |||||||
 | |||||||
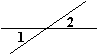A、 B、 C、 D、
10、在图10中，直线AB、CD相交于点O，OE⊥AB于O，∠DOE=55°，则∠AOC的度数为 ( )
A、 40° B、 45° C、 30° D、35°
 |
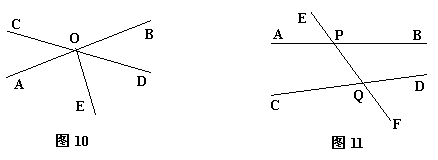11、如图11中，两条非平行直线AB、CD被第三条直线EF所截，交点为P、Q，那么这三条直线将所在平面分成 ( )
A 、5个部分 B、6个部分 C、7个部分 D)、8个部分
12、如图，AB∥CD，AC⊥BC，图中与∠CAB互余的角有 （ ）
A：1个 B：2个 C：3个 D：4个
13、已知，如图，下列条件中不能判断直线l1∥l2的是（ ）
A、∠1＝∠3 B 、∠2＝∠3 C、∠4＝∠5 D、∠2＋∠4＝180°
 |
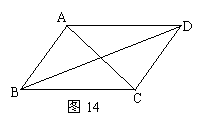
14、如图14中，AB∥CD，AD∥BC有多少组相等的内错角（ ）
A、两组 B、三组 C、四组 D、五组
15、如图15中，已知△ABC中，AB∥EF，DE∥BC，则图中相等的同位角有（ ）
相等的内错角有（ ）
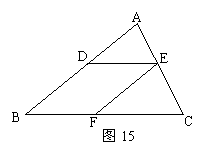
A、2组 B、三组 C、四组 D、五组
三、解答题
1、已知：
，求
的值
2、已知
 |
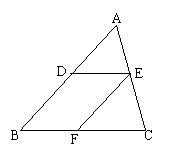3、如图：已知AB∥EF，DE∥BC，
则∠ADE=∠EFC吗？为什么？
 |
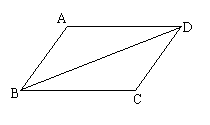4、如图：AB∥CD，AD∥BC，问：
∠ABC=∠CDA吗？为什么？
 |
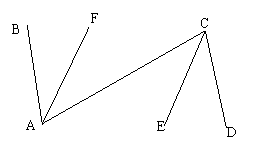5、如图：已知AB∥CD，AF平分∠BAC
CE平分∠ACD，则AF∥CE成立吗？
为什么？