霞浦中学2004学年第一学期期中质量调研七年级数学试题
班级 姓名 分数
一、 填一填（第4题3分，9、10、11、12每题2分，其余每空1分，计26分）
1．圆柱体有 个面，侧面展开图是 形．
2．写出任意两个大于-1的负数______、______．
3．-2３的底数是_______,指数是_______．
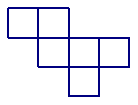4．在如图所示的六个方格中,分别填入下列各数,使围成正方体后相对两面的两个数互为倒数.(填写各数的序号即可) ．
①-2 ②4 ③
④8 ⑤
⑥
5．代数式
共有______项,其中第2项的
系数是_____ _．
6．若
与
是同类项，则m= , n= ．
7．有理数0，2，－7, 
,3.14, 
,－3, －0.75中,负整数是
,分数是
．
8．根据规律填上合适的数：(1) 1，4，9，16， ,36；
(2) 2，5，10，17， ，37,_____ ．
9．数轴上表示－2的点先向右移动3个单位，再向左移动5个单位，则此时该点表示的数是_____ __．
10．a的平方的一半与b平方的差,用代数式表示为___________________．。
11．已知a、b互为相反数,c、d互为倒数, 
=－3.则代数式
的值为________．
12．对有理数a、b,定义运算a*b=
,则3*4=________．
二．选一选（每题2分，共16分）
13．下列各图经过折叠后不能围成一个正方体的是……………………（ ）
A B C D
14．下列说法不正确的是…………………………………………………( )
A．1是绝对值最小的数； B．0既不是正数，也不是负数；
C．一个有理数不是整数就是分数； D．0的绝对值是0．
15．若a－b－c=a-( )成立，则括号应填入………………………（ ）
A． b－c； B． b+c； C． －b+c ； D． －b－c．
16．下面各组数中，相等的一组是…………………………………………( )
A．
与
； B．
与
；C．
与
； D．
与
．
17．观察下列算式：
，
，
，则a、b、c的大小关系是………………………………………………………………………（ ）
A．b>c>a； B．a >c>b ； C．a>b>c； D． c>b>a．
18．若
，则
的值为……………………………（ ）
A．1 ； B. －1 ； C. 3； D. －3．
19．某种细菌在培养过程中，每半小时分裂1次，每次一分为二．若这种细菌由1个分裂到16个，那么这个过程要经过…………………………………( )
A．1.5小时； B．2小时； C．3小时； D．4小时．
20．用不用的方法将长方体截去一个角，在剩下的各种几何体中，顶点最多的个数以及棱数最少的条数分别为…………………………………………（ ）
A．9个，12条； B．9个，13条 ； C．10个，12条 ； D．10个，13条
三．解解看
21．如图所示是由几个小立方块所搭的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，请画出相应几何体的主视图和左视图：（每个图2分，计4分）
22．有理数运算．（每题4分，计16分）
（1）
（2）
（3）
（4）
23．化简、求值，列式计算．（每题4分，计12分）
（1）
（2）被减式是
，差是
，求减式是多少？
（3）
，其中a=－1．
24．某空调器销售商，今年四月份销出空调（a-1）台，五月份销售空调比四月份的2倍少1台，六月份销售空调比前两个月的总和的4倍还多5台．
（1）用代数式表示该销售商今年第二季度共销售空调多少台？（3分）
（2）若a=220，求第二季度销售的空调总数．（2分）
25． “十.一”黄金周期间，某风景区在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）：（7分）
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人数变化(万人) | ＋1.6 | ＋0.8 | ＋0.4 | －0.4 | －0.8 | ＋0.2 | －1.2 |
(1)若9月30日的游客为3万人，请完成下面7天游客人数记录表：
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 游客人数 (万人) | 4.6 |
(2)七天内游客人数最多的一天有 万人；游客人数最少的一天是第 天．
26．树的高度与树生长的年数有关，测得某棵树的有关数据如下表（树苗原高100厘米）：
| 年数a | 高度h（单位：厘米） |
| 1 | 115 |
| 2 | 130 |
| 3 | 145 |
| 4 | |
| … | …… |
（1）填出第4年树苗可能达到的高度；（2分）
（2）请用含a的代数式表示： a年后树的高度h=____ ________；（2分）
（3）根据这种长势，10年后这棵树可能达到的高度是 厘米．（2分）
27．探索规律
观察下面由※组成的图案和算式，解答问题：
1+3=4=22
1+3+5=9=32
1+3+5+7=19=42
1+3+5+7+9=25=52
（1）请猜想1+3+5+7+9+…+19= ；（2分）
（2）请猜想1+3+5+7+9+…+（2n-1）+（2n+1）+（2n+3）= ；（3分）
（3）请用上述规律计算：（3分）
103+105+107+…+2003+2005
创新拓展：（101、102班同学必做，其他各班同学不用做）
1、已知
，则x=
．
2、若有理数在数轴上的位置如图所示，则化简
．
3、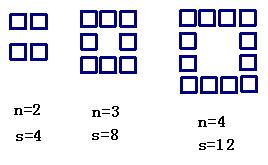
观察右面的图案，每条边上有n
（n≥2）个方点，每个图案中方点的总数
是S.
（1）请写出n=5时， S= ；
（2）请写出n=18时，S= ；
（3）按上述规律，写出S与n的关系式
S= ．
4、计算：
．
5、某地出租车收费标准是：起步价10元，可乘3千米。3千米到5千米，每千米价1．8元；5千米后，每千米价格2．7元．
（1）若某人乘坐了5千米的路程，请写出他应支付的费用；
（2）若他支付了19元车费，你能算出他乘坐的路程吗？
6、某织布厂有工人200名，为改善经营，增设制衣项目，已知每人每天能织布30米，或利用所织布制衣4件，制衣一件用布1.5米，将布直接出售，每米布可获利2元；将布制成衣后出售，每件可获利25元，若每名工人一天只能做一项工作，且不计其他因素，设安排x名工人制衣，则：
（1）一天中制衣所获得的利润为P= （用含的代数式表示）
（2）一天中剩余布出售所获利润为Q= （用含的代数式表示）
（3）当安排166名工人制衣时，所获总利润W（元）是多少？能否安排167名工人制衣以提高利润？试说明理由.