习题精选
一、填空题
1.方程![]() 的解为____________.
的解为____________.
2.已知![]() 是方程
是方程![]() 的解,则
的解,则![]() =_______________.
=_______________.
3.由![]() ,得
,得![]() ,理由是;在方程的两边同时加上_________,或者根据被减数=__________+___________.
,理由是;在方程的两边同时加上_________,或者根据被减数=__________+___________.
4.由![]() ,得
,得![]() ,理由是:在方程的两边同时乘以_______.或者根据乘=__________÷_________.
,理由是:在方程的两边同时乘以_______.或者根据乘=__________÷_________.
5.解方程![]() ,第一步在方程两边同时_________,得到方程________;第二步在新方程的两边同时__________,得到
,第一步在方程两边同时_________,得到方程________;第二步在新方程的两边同时__________,得到![]() __________.
__________.
6.当![]() _________时,代数式
_________时,代数式![]() 的值与
的值与![]() 互为倒数.
互为倒数.
7.若![]() 的值比
的值比![]() 的值大10,则
的值大10,则![]() _________.
_________.
8.若关于![]() 的方程
的方程![]() 的解是
的解是![]() .则
.则![]() _________.
_________.
9.设![]() 与
与![]() 都是自然数,且
都是自然数,且![]() ,则满足条件的
,则满足条件的![]() 的值是________.
的值是________.
10.关于![]() 的方程
的方程![]() 的根是
的根是![]() ,则
,则![]() 等于__________.
等于__________.
11.若关于![]() 的方程的解为
的方程的解为![]() 的解为
的解为![]() ,
,![]() ,
,![]() 为质数,且
为质数,且![]() ,则
,则![]() ________,
________,![]() ________.
________.
参考答案:
1.![]() ;2.2;3.2,差,减数;
;2.2;3.2,差,减数;
4.![]() ,积,另一个乘数;
,积,另一个乘数;
5.减去2 ![]() 乘以
乘以![]() 4;
4;
6.1;7.6;8.![]() ;
;
9.0,1,2,3,4,5;
10.3;11.2109
二、选择题
1.下列各式属于方程的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.下列判断:(1)![]() 是方程
是方程![]() 的解.(2)方程
的解.(2)方程![]() 的解是
的解是![]() .(3)方程
.(3)方程![]() 的解是
的解是![]() .
.![]() 是方程的解.其中正确的个数是( ).
是方程的解.其中正确的个数是( ).
A.4 B.3 C.2 D.1
3.长方形的周长为22cm,长比宽长5cm,若设长方形的宽为![]() cm,则方程可列为( ).
cm,则方程可列为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.方程![]() 的解是( ).
的解是( ).
A.l和2 B.0和1 C.0和2 D.0、1和2
5.若![]() 是方程
是方程![]() 的解,则
的解,则![]() 的值为( ).
的值为( ).
A.144 B.72 C.24 D.12
6.与方程![]() 的解完全相同的方程是( ).
的解完全相同的方程是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
参考答案:
1.A 2.C 3.D 4.A 5.C 6.D
三、解答题
1.下列各式中哪些是方程,哪些不是方程:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥
;⑥![]() .
.
2.解方程:(1)![]() ;(2)
;(2)![]() .
.
3.某校购买篮球和排球共花去600元,篮球每个45元,排球每个30元,已知篮球买了10个,问排球买了多少个?
4.一个两位数,十位数字比个位数字的2倍大1,它们的数字之和为10,求这个两位数.
5.某工程甲单独做要12天完成,乙单独做要15天完成,若甲先做3天,然后乙加入同时做,问这项工程乙加入后还要多少天完成?
6.甲、乙两队共有工人87人,如果从乙队调出5人给甲队,那么甲队人数正好是乙队人数的2倍,求甲、乙两队的人数.
7.甲、动两地相距7千米,某人从甲地出发前往乙地.他先以6千米/时的速度匀速步行,后以9千米/时的速度匀速跑步,结果恰用1小时到达了乙地.求此人步行和跑步的时间.
8.用一队卡车运一批货物,若每辆卡车装7吨货物,则尚余10吨货物装不完;若每辆卡车装8吨货物,则最后一辆卡车只装3吨货物就装完了这批货物.求这批货物有多少吨?
10.某种商品的进货价为每件![]() 元,零售价为每件1100元,若按商品零售价的80%降价出售,仍可获利10%(相对于进货价),问进货价
元,零售价为每件1100元,若按商品零售价的80%降价出售,仍可获利10%(相对于进货价),问进货价![]() 为多少元?
为多少元?
11.甲、乙两列客车的长分别为150米和200米,它们相向行驶在平行的轨道上,已知甲车上某旅客测得乙车在他窗口外经过的时间是10秒,那么乙车上的乘客看见甲车在他窗口经过的时间是多少秒?
12.甲、乙二人从相距30m的两地同向而行,甲每秒走7m,乙每秒走6.5m,如果甲先出发1秒钟后,乙才出发,求甲出发后几秒钟追上乙?
13.如图,是某风景区的旅游路线示意图,其中![]() 、
、![]() 、
、![]() 为风景点,
为风景点,![]() 为两条路的交叉点,图中数据为相应两点间的路程(单位:千米).一学生从A处出发,以2千米/小时的速度步行游览,每个景点的逗留时间均为0.5小时.
为两条路的交叉点,图中数据为相应两点间的路程(单位:千米).一学生从A处出发,以2千米/小时的速度步行游览,每个景点的逗留时间均为0.5小时.
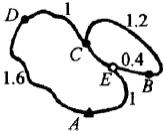
(1)当他沿着路线A→D→C→E→A游览回到![]() 处时,共用了3小时,求
处时,共用了3小时,求![]() 的长;
的长;
(2)若此学生打算从![]() 处出发后,步行速度与在景点的逗留时间保持不变,且在最短时间内看完三个景点返回到
处出发后,步行速度与在景点的逗留时间保持不变,且在最短时间内看完三个景点返回到![]() 处,请你为他设计一条步行路线,并说明这样设计的理由(不考虑其他因素).
处,请你为他设计一条步行路线,并说明这样设计的理由(不考虑其他因素).
参考答案:
1.由方程的定义:则①、②、⑥是方程,而③、④、⑤不是方程.
2.(1)![]() ;
;![]() .
.
3.设买了![]() 个排球,根据题意,得
个排球,根据题意,得![]() ,
,![]() ,解得
,解得![]() .
.
4.设个位数字为![]() ,依题意为:
,依题意为:![]() ,解得
,解得![]() ,故这个两位数为73.
,故这个两位数为73.
5.设乙加入后还要![]() 天完成,依题意有:
天完成,依题意有:![]() ,解得
,解得![]() .
.
6.设乙队有![]() 人,则
人,则![]() ,
,![]() ,故甲队有53人.
,故甲队有53人.
7.设步行![]() 小时,则有
小时,则有![]() ,解得;
,解得;![]() ,则跑步时间为
,则跑步时间为![]() 小时.
小时.
9.设卡车有![]() 辆,则
辆,则![]() ,
,![]() ,则货物有
,则货物有![]() (吨).
(吨).
10.800元.
11.由题意知甲、乙两车速度和为![]() (米/秒),故乙车上的乘客看到甲车在他窗口驶过的时间为
(米/秒),故乙车上的乘客看到甲车在他窗口驶过的时间为![]() (秒).
(秒).
12.![]() (秒).
(秒).
13.可依A→D→C→E→A的行走路径构造方程来解之.
(1)设![]() 的长为
的长为![]() 千米,依题意得
千米,依题意得![]() ,解得
,解得![]() .
.
(2)若步行路线为A→D→C→E→A(或A→E→B→C→D→A),则所用时间为:
![]() (小时).
(小时).
若步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A),则所用时间为:
![]() (小时).
(小时).
因此,步行路线应为:A→D→C→E→B→E→A(或A→E→B→E→C→D→A).
典型例题
例1 判断下列各式哪些是方程,哪些不是方程.
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
分析:本题考查对方程的概念的理解.判断一个式于是否是方程需满足以下两个条件:(1)含有本知数;(2)是一个等式.以此去分析(l)至(4)小题即可.
解:(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() 都不是方程;(4)
都不是方程;(4)![]() 都是方程.
都是方程.
说明:本题意在使大家明确方程与恒等式、代数式这三者的区别.
例2 判断![]() 是否是方程
是否是方程![]() 的解.
的解.
分析:判断所给数值是否为方程的解有两种方法:一是解方程求出方程的解;二是根据方程的解的定义,方程的解应使方程左、右两边相等.所以我们把所给数值代入原方程检验也可.因为此题所给方程不是简易方程,所以目前我们只能选取第二种方法.
解:把![]() 分别代入方程的左边和右边.
分别代入方程的左边和右边.
左边![]()
右边![]()
左边≠右边,
∴![]() 不是方程
不是方程![]() 的解.
的解.
例3 解下列方程:
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ; (4)
; (4)![]() ;
;
(5)![]() (其中
(其中![]() 为未知数,
为未知数,![]() 均为已知数,且
均为已知数,且![]() )
)
分析 到目前为止,我们已经学过两种方法,解简易方程:小学的算术解法和现在学的代数解法.本题我们采用现在学的代数解法.
解:(1)![]() ,
,
![]() .(方程两边同时减去4)
.(方程两边同时减去4)
(2)![]() ,
,
![]() .(方程两边同时乘以4)
.(方程两边同时乘以4)
(3)![]() ,
,
![]() ,(方程两边同时加上5)
,(方程两边同时加上5)
![]() . (方程两边同时除以2)
. (方程两边同时除以2)
(4)![]() ,
,
![]() .(方程两边同时加上2)
.(方程两边同时加上2)
![]() .(方程两边同时乘以3)
.(方程两边同时乘以3)
(5)![]() ,
,
![]() , (方程两边同时加上
, (方程两边同时加上![]() )
)
![]() . (方程两边同时除以
. (方程两边同时除以![]() )
)
说明:(2)、(4)两小题.在最后一步求![]() 的值时都是乘以分母上的数,这点容易出错.(5)题是含有字母已知数的方程,做题时要随时分清谁是本知数,谁是已知数.解方程后检验的步骤可不写,但一定要养成自我检验的习惯.
的值时都是乘以分母上的数,这点容易出错.(5)题是含有字母已知数的方程,做题时要随时分清谁是本知数,谁是已知数.解方程后检验的步骤可不写,但一定要养成自我检验的习惯.
例4 已知是方程![]() 是方程
是方程![]() 的解,求
的解,求![]() 的值.
的值.
解:由已知,![]() 是原方程的解,
是原方程的解,
得 ![]() ,
,
![]() ,
,
![]() .
.
答:![]() 的值为30.
的值为30.
说明:本例体现了一种“代换”的思想和“待定系数法”的思想,要注意理解并掌握.
例5 已知某厂今年平均每月生产机器80台,比去年平均每月生产机器的1.5倍少13台,求去年平均每月生产机器多少台?
解:设去年平均每月生产机器![]() 台,则今年生产机器(
台,则今年生产机器(![]() )台.
)台.
由题意,得![]() ,
,
![]() ,
,
![]() .
.
答:去年平均每月生产机器62台.
说明:列方程首先应设好未知数,弄清已知和未知的量,把未知的量列成关于![]() 的代数式.列方程最关键是要挖掘题目中的等量关系,一般有两类,一类是题目中固有的,另一类是数量内在固有的等量关系.
的代数式.列方程最关键是要挖掘题目中的等量关系,一般有两类,一类是题目中固有的,另一类是数量内在固有的等量关系.
例6 甲队有54人,乙队有66人,问从甲队调给乙队几人能使甲队人数是乙队人数的![]() ?
?
分析:此题必须弄清:一、甲、乙两队原来各有多少人;二、变动后甲、乙两队各有多少人(注意:甲队减少的人数正是乙队增加的人数);三、题中的等量关系是:变动后甲队人数是乙队人数的![]() ,即变动后甲队人数的3倍等于乙队人数.
,即变动后甲队人数的3倍等于乙队人数.
解:设从甲队调给乙队x人,
则变动后甲队有![]() 人,乙队有
人,乙队有![]() 人,根据题意,得:
人,根据题意,得:![]()
![]() ,
,
![]()
答:从甲队调给乙队24人.
选题角度:
大体分这几类:1.用方程的概念,判断哪些是方程,哪些不是方程;2.判断所给数值是否为方程的解;3.根据方程的解求方程的系数;
4.列出简易方程,解决实际问题的应用题.