典型例题
例1 计算下列各题：
（1）
；（2）
；
（3）
；（4）
；
（5）
；（6）
．
分析：按有理数乘法法则进行计算：第(6)题是两个相反数的积，注意与相反数的和进行比较．
解：（1）
；
（2）
；
（3） 
；
（4）
；
（5）
；
（6）
．
说明：在进行有理数乘法运算时，除了要熟练掌握乘法法则之外，还应当注意以下两点：1．一个数乘以1等于它本身，一个数乘以－1等于它的相反数．2．两个相反数的和与积是完全不同的两个结果，不要混淆．
例2 判断题(对的入“T”，错的入“F”)
(1) 同号两数相乘，符号不变．( )
(2) 异号两数相乘，取绝对值较大的因数的符号．( )
(3) 两数相乘，如果积为正数，则这两个因数都为正数．( )
(4) 两数相乘，如果积为负数，则这两个因数异号．( )
(5) 两数相乘，如果积为0，则这两个数全为0．( )
(6) 两个数相乘，积比每一个因数都大．( )
(7) 如果
＞0，且＋＜0，则＜0，＜0．( )
(8) 如果 ＜0，则＞0，＜0．( )
(9) 如果 =0，则，中至少有一个为0．( )
解：(1) F．同号两数相乘，符号为正．
(2) F．异号两数相乘，符号为负，与绝对值的大小无关．
(3) F．这两个因数也可以都为负数．
(4) T．
(5) F．两数相乘积为0，两数中可以有一个不为0．
(6) F．不一定，例如异号两数相乘时，积就比正因数小．
(7) T．
(8) F．当ab＜0时，也可能是a＜0，b＞0．
(9) T．
说明：本题应用有理数乘法法则进行判断，两数相乘，同号得正，异号得负，并把绝对值相乘．任何数同0相乘，都得0．
例3 填空题：
(1) 五个数相乘，积为负，则其中正因数有____个．
(2) 四个各不相等的整数，，
，
，它们的积 
=25，那么＋＋＋ =____．
分析：(1)五个数相乘积为负，说明五个数中，负因数的个数是1个，3个或5个．(2)因为25=1×5×5，又，， ， 是四个各不相等的整数，所以这四个数只能是±1和±5．
解：(1) 五个数相乘积为负，说明五个数中，负因数的个数为奇数，
即1个，3个或5个．
∴正因数有4个，2个或0个．
(2) ∵， ， ， 是四个各不相等的整数，且 =25=1×5×5，
∴ ， ， ， 只能是＋1，-1，＋5，-5这四个数．
∴ ＋
＋
＋ =0．
说明：解例3的理论依据是：几个不等于0的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负；当负因数有偶数个时，积为正．几个数相乘，有一个因数为0，积就为0．
例4 填空题：
（1）
__________；
（2）
__________；
（3）
__________．
分析：(1)是4个不为0的数相乘，0.01×100=1，要注意小数点的位置；(2)是4个数相乘，其中有一个因数是0；（3）因为
，三个分数的分子均为7，所以同时正用又逆用乘法分配律才是最佳的解题方法．
解：（1）
；
（2） 
；
（3）
例5 计算：
．
分析：这是5个非0的数相乘，其中有3个负因数，应当先确定积的符号，然后把绝对值相乘．绝对值相乘时，要注意运用乘法的交换律和结合律，此题把小数化为分数计算较简便．
解：原式
说明：几个不为0的数相乘时，确定积的符号是第一步，要使计算简便，关键在绝对值的计算．求积的绝对值时要注意运用乘法交换律和结合律；当因数是小数时，一般要化为分数再相乘；当因数是带分数时，要化为假分数再相乘；在化简时，能约分的要约分．
例6 计算
．
分析：此题若直接相乘很麻烦，根据它的特点：可以把被乘数拆成两项，然后用乘法分配律计算．
解：
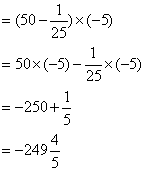
说明：
（1）此题利用分解思想把
拆成
，然后运用分配律，可使运算简便，这是一个重要的方法技巧．（2）不要漏项，即可把乘数与括号内的每一项都相乘．
（3）相乘时，符号不要弄错．
例7 把下图中输入的每一个数，各乘以-3，得到输出的数。
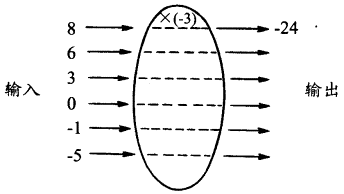
解：略
说明：在进行有理数乘法运算时，除了要熟练掌握乘法法则之外，还应当注意以下两点：1．一个数乘以1等于它本身，一个数乘以－1等于它的相反数．2．两个相反数的和与积是完全不同的两个结果，不要混淆．
习题精选
一、选择题
1．如果两上有理数在数轴上的对应点在原点的同侧，那么这两个有理数的积（ ）．
（A）一定为正数 （B）一定为负数
（C）为零 （D）可能为正数也可能为负数
2．若干个不等于0的有理数相乘，积的符号（ ）．
（A）由因数的个数决定 （B）由正因数的个数决定
（C）产因数的个数决定 （D）由负因数的大小决定
3．1000个有理数相乘的积为0，那么（ ）．
（A）每 数一定都是零 （B）每个因数都不为零
（C）至少有一个因数不为零 （D）至少有一个因数为零
4．一个数和它的相反数的积是（ ）．
（A）正数 （B）负数 （C）一定不小于0 （D）一定不大于0
5．若
，则
必定满足（ ）．
（A）
（B）
（C）或 （D）无法确定
6．若
，则以下结论中，正确的是（ ）．
（A）
（B）
（C）
且
（D）
中至少有一个为零
7．如果
满足
且 ，则下列各式中，正确的是（ ）．
（A）
（B）
（C）且
（D） 异号，且正数的绝对值较大
8．以下命题正确的是（ ）．
（A）如果
那么a、b都为零
（B）如果
,那么a、b不都为零
（C）如果
，那么a、b都为零
（D）如果
，那么a、b均不为零
二、填空题
1．
__________；
2．
__________；
3．
__________；
4．当两数__________时，它们的和为0；
5．当两数__________时，它们的积为0；
6．当两数__________时，它们的积为1；
7．
＝__________；
8．
__________；
9．
__________；
10．
__________．
三、解答题
1.计算：
（1）
；
（2）
；
（3）
；（4）
；
（5）
；（6）
；
（7）
；（8）
；
（9）
；（10）
；
（11）
；（12）
；
（13）
；
（14）
；
（15）
；（16）
．
2.根据已知条件列式计算：
（1）某数的
等于
，求这个数；
（2）
的多少倍等于
．
3.已知
．试求下列各代数式的值．
（1）
；（2）
．
4．若
求
的值．
5．求
的积．
6．已知
与2互为相反数，
互为倒数，试求代数式
的值．
参考答案：
一、1．A 2．C 3．D 4．D 5． C 6．D 7．D 8．A
二、1．12；2．10；3．
；4．0或1；5．0；
6．0；7．；8．
；9．
；10．6．
三、（1）
；（2）0；（3）687；（4）－97902；（5）
；（6）
；
（7）4；（8）－6.91；（9）－526.5；（10）－1074；（11）
；（12）
；
（13）
；（14）100；（15）
；（16）
．
2．（1）
；（2）
．
3．（1）
；（2）
．
4．分两种情况讨论：（1）
时，原式=
（2）
时，原式=
故原式=-1．
5．
．
6．
．