典型例题
例1(1)求单项式 ![]() 、
、
![]() 、
、
![]() 、
、
![]() 的和;
的和;
(2)求单项式 ![]() 、
、
![]() 、
、
![]() 的和与
的和与
![]() 的差.
的差.
解:(1) ![]() (列式)
(列式)
![]() (去括号)
(去括号)
![]() ;(合并同类项)
;(合并同类项)
(2) ![]() (列式)
(列式)
![]() (去小括号)
(去小括号)
![]() (合并同类项)
(合并同类项)
![]() (去中括号)
(去中括号)
![]() (合并同类项)
(合并同类项)
说明: 求若干个单项式和与差的步骤,一般有列式,去括号,合并同类项三步,要注意每一步运算的根据,做到步步有理有据,以保证运算的正确性.
选题角度:关于求单项式和的题目
例2 (1)求多项式 ![]() 与
与
![]() 的和;
的和;
(2)求多项式 ![]() 与
与
![]() 的差.
的差.
解:(1) ( ![]() )+(
)+( ![]() )
)
![]()
![]() ;
;
(2)
( ![]() )-(
)-(
![]() )
)
![]()
![]()
说明: 本题是求两个多项式的和与差,列式时都要添上括号,把每个多项式分别括起来,再用加减连接;运算时,按去括号法则,先去掉括号,再合并同类项.
选题角度:关于求两个多项式和的题目
例3 计算 :
(1) ![]() ;
;
(2) 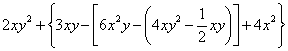
分析: 由于题中有多重括号,所以要依次去括号,边去括号边合并同类项,以简便运算.
解:(1) ![]()
![]()
![]()
![]()
![]() ;
;
(2) 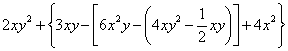
![]()
![]()
![]()
![]()
![]()
说明: 有多重括号时,一般先从内层括号开始,先去掉小括号,合并同类项;再去中括号,合并同类项;最后去大括号,合并同类项.一层一层地去括号不会发生混乱,去括号时一定要注意符号的变号.
选题角度:关于去掉多重括号,进行计算的题目
例4 求 ![]() 、
、
![]() 的和与
的和与
![]() 的差.
的差.
分析:此题相当于这样的问题:已知两数的和减去第三个数,求它们的差,由此,我们可先列出相应的代数式,再用整式加减的法则求解.
解:( ![]() )+(
)+(
![]() )-(
)-(
![]() )
)
![]()
说明:求若干个整式的和或差,要先用括号把第一个整式括起来,再用加减号连接,然后用去括号法则去括号,最后合并同类项.
选题角度:关于求多项式的和,再求差的题目
例5 求代数式的值:
![]() ,
,
其中 ![]() .
.
分析:对于此类题,一定要先化简,再代入化简后的式子中求值,化简的过程就是整式加减的运算过程.
解:原式= ![]()
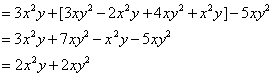
当 ![]() 时,
时,
原式= ![]()
= ![]()
= ![]()
说明:代数式的值是由所含字母的取值决定的.因此,不能笼统地说代数式的值等于多少 ,应当说明所含字母的取值是多少,另外,要熟练掌握此类题的解题规范.
选题角度:关于先化简,再求值的题目
例6 已知 ![]()
求 ![]() 的值.
的值.
分析:任何有理数的偶次幂、绝对值都是非负数,如果这样的两个非负数和为零,那么它们必须都等于零,由此求出a,b的值,再代入,为了简化运算过程,在代入前应先化简.
解:∵ ![]() ,
,
![]() ,
,
由已知 ![]() ,
,
∴ ![]() 且
且
![]() .
.
∴ ![]()
而 原式= ![]()
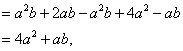
当 ![]() 时,
时,
原式= ![]()
![]()
选题角度:关于先化简已知式子,求得字母的值,再把要求的式子化简求值
习题精选
一、填空题
1. ![]() 与多项式
与多项式
![]() 的和是_______,多项式
的和是_______,多项式 ![]() 与多项式
与多项式![]() 的差是________.
的差是________.
2.化简: ![]()
![]()
3. ![]()
二、选择题
1.两个次多项式的差是( )
A.六次多项式 B.十二次多项式
C.不高于六次的代数式 D.以上都不对
2.长方形的周长为 ![]() ,一边长为
,一边长为
![]() ,则另一边长为( )
,则另一边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3.若 ![]() ,则
,则
![]() 的值为( )
的值为( )
A.18 B.20 C.19 D.无法求出
4.若 ![]()
![]() ,则
,则
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.将多项 ![]() 写成两个二项式的差,下列写法错误的是( )
写成两个二项式的差,下列写法错误的是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]() (△)
(△)
6.若 ![]() ,
,
![]() ,则
,则
![]() 的值( )
的值( )
A.等于4 B.等于-4
C.不能确定 D.等于 ![]() (△)
(△)
三、解答题
1.化简求值:
(1) ![]() ,其中
,其中
![]() ;
;
(2) ![]() ,其中
,其中
![]() ;
;
(3) ![]() ,其中
,其中
![]() ;
;
(4) ![]() ,其中
,其中
![]() ;
;
(5) ![]() ,其中
,其中
![]() ;
;
(6) ![]() ,其中
,其中
![]() .
.
2.(1)已知
![]() ,
,
求
![]() 的值;
的值;
(2)已知 ![]() ,
,
求
![]() 的值;
的值;
(3)已知 ![]() ,
,
求
![]() 的值.
的值.
3.计算:(1) ![]()
(2) ![]()
4.(1)求多项式
![]() 与
与
![]() 的差.
的差.
(2)求多项式 ![]() 与
与
![]() 的差.
的差.
5.若一个多项式的 ![]() 与多项式
与多项式
![]() 的和为
的和为
![]() ,求这个多项式,并求出当
,求这个多项式,并求出当
![]() 时这个多项式的值.
时这个多项式的值.
6.已知m、n为常数,且 ![]() 与
与
![]() 的差不含二次项,求m、n的值,并求出这两个多项式的差.
的差不含二次项,求m、n的值,并求出这两个多项式的差.
7.某同学把一个整式减去多项式 ![]() 误认为加上这个多项式,结果答案为:
误认为加上这个多项式,结果答案为:
![]() ,求原题的正确答案.
,求原题的正确答案.
8.计算:(1) ![]()
(2) ![]()
9.一个多项式加上多项式 ![]() 的2倍得多项式
的2倍得多项式 ![]() ,求这个多项式.
,求这个多项式.
10.已知 ![]() ,化简
,化简
![]() ,并求出它的值.
,并求出它的值.
11.代数式 ![]() 与多项式
与多项式
![]() 的差与字母x的取值无关,求代数式
的差与字母x的取值无关,求代数式 ![]() 的值.
的值.
12.今年初,共青团中央等发起了“保护母亲河的捐款活动”.某校初一两个班的115名学生积极参与,踊跃捐款,已知甲班 ![]() 的学生每人捐10元,乙班
的学生每人捐10元,乙班 ![]() 的学生每人捐10元,两班其余学生每人捐5元,设甲班有学生x人,试用代数式表示两班捐款的总额,并进行化简.
的学生每人捐10元,两班其余学生每人捐5元,设甲班有学生x人,试用代数式表示两班捐款的总额,并进行化简.
13.A、B两家公司都准备向社会招聘人才,两家公司条件基本相同,只有工资待遇有
如下差异:A公司,年薪两万元,每年加工龄工资400元;B公司,半年薪一万元,每半年加式龄工资100元,求A、B 两家公司第n年的年薪分别是多少?从经济收入的角度考虑的话,选择哪家公司有利?A、B两家公司收入每年相差多少?(△)
参考答案:
一、1. ![]()
![]()
2. ![]()
![]()
3. ![]()
二、1.C 2.C 3.C 4.D 5.C 6.D
三、1.(1)-12;(2) ![]() ;(3)49;(4)
;(3)49;(4) ![]() ;(5)-3;(6)
;(5)-3;(6) ![]()
2.(1)提示:根据非负数的性质:非负数的和为零,这两个非负数同时为零,求出
![]() 的值,然后代入求值.值为
的值,然后代入求值.值为
![]() ;(2)6;(3)
;(2)6;(3) ![]()
3.(1)
![]() (2)
(2) ![]()
4.(1)
![]() (2)
(2) ![]()
5. ![]() -80
-80
6. ![]()
![]()
![]()
7. ![]()
8.(1)
![]() (2)
(2) ![]()
9. ![]()
10.105
11. ![]() 中
中
![]() ∴
∴
![]()
![]() 代入后求值为
代入后求值为
![]() 12.
12. ![]()
13.A公司收入为:
![]() B公司收入为:
B公司收入为:
![]() 显然选择B公司,B公司比A公司每年高100元.
显然选择B公司,B公司比A公司每年高100元.