填空题
1.用字母表示三个奇数的和____________.
2.![]() 的2倍与3的差____________.
的2倍与3的差____________.
3.![]() 的平方的5倍与
的平方的5倍与![]() 的和____________.
的和____________.
4.比![]() 、
、![]() 的积的
的积的![]() 小7的数____________.
小7的数____________.
5.李明有![]() 本教科书,课外书比教科书多
本教科书,课外书比教科书多![]() 本,那么他共有____________本书.
本,那么他共有____________本书.
6.一件上衣售价为![]() 元,降价10%后的售价为____________.
元,降价10%后的售价为____________.
7.某商品利润是![]() 元,利润率是20%,此商品的进价是____________元.
元,利润率是20%,此商品的进价是____________元.
8.一项工程,甲队单独完成要![]() 天,乙队单独完成要
天,乙队单独完成要![]() 天,两队合作需要____________天完成.
天,两队合作需要____________天完成.
9.“![]() 除以
除以![]() 的商的平方与
的商的平方与![]() 减去
减去![]() 的差的和”用代数式表示是____________.
的差的和”用代数式表示是____________.
参考答案:
1.设![]() 为自然数,则三个连续
为自然数,则三个连续![]() 的奇数和为
的奇数和为
2. ![]() 3.
3.![]() 4.
4.![]()
5.![]() 6.
6.![]() 元 7.
元 7.![]() 8.
8.![]() 9.
9.![]()
选择题
1.三个连续的偶数中若中间的一个是![]() ,是代数式表示其它两个偶数是( ).
,是代数式表示其它两个偶数是( ).
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2.某钢铁厂每天生产钢铁![]() 吨,现在每天比原来增加
吨,现在每天比原来增加![]() ,现在每天钢铁的产量是( )吨.
,现在每天钢铁的产量是( )吨.
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
3.下列各式:(1)![]() (2)
(2)![]() (3)
(3)![]() ( 4)
( 4)![]() (5)
(5)![]() (6)
(6)![]() 其中代数式的个数为( ).
其中代数式的个数为( ).
A.2 B.3 C.4 D.5
4.代数式![]() ,用语言叙述正确的是( ).
,用语言叙述正确的是( ).
A.![]() 与
与![]() 的平方差
B.
的平方差
B.![]() 的平方减 5乘以
的平方减 5乘以![]() 的平方
的平方
C.![]() 的平方与
的平方与![]() 的平方的5倍的差 D.
的平方的5倍的差 D.![]() 与
与![]() 的差的平方
的差的平方
5.下列各式:(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)![]() (6)
(6)![]() 其中不符合代数式书写要求的有( ).
其中不符合代数式书写要求的有( ).
A.5个 B.4个 C.3个 D.2个
6.关于代数式![]() 的意义,下列说法中不正确的是( ).
的意义,下列说法中不正确的是( ).
A.比![]() 的平方少1的数 B.
的平方少1的数 B.![]() 的平方与1的差
的平方与1的差
C.![]() 与1两数的平方差 D.
与1两数的平方差 D.![]() 与1的差的平方
与1的差的平方
7.下面各判断后面的代数式中错误的是( ).
A.![]() 的3倍与
的3倍与![]() 的2倍的和为
的2倍的和为![]() B.
B.![]() 除以
除以![]() 的商与2的差的平方为
的商与2的差的平方为![]()
C.![]() 、
、![]() 两数和乘以
两数和乘以![]() 、
、![]() 两数差为
两数差为![]() D.
D.![]() 与
与![]() 的和的
的和的![]() 为
为![]()
参考答案:1. C 2.D3.B 4.C 5.B 6.D 7.D
解答题
1.下列各式哪些是代数式,哪些不是代数式.
(1)![]() ;
(2)
;
(2)![]() ; (3)
; (3)![]() ; (4)
; (4)![]() ;
;
(5)3; (6)![]() ; (7)
; (7)![]() ; (8)
; (8)![]()
2.省略下列各式中的“×”号或“÷”号:
(1)![]() ;(2)
;(2)![]() ;
;
(3)![]() ;(4)
;(4)![]() ;
;
(5)![]() ; (6)
; (6)![]() ;
;
(7)![]() ;(8)
;(8)![]() ;
;
3.用字母表示:(1)所有的奇数;(2)所有的偶数;(3)所有能被3整除的数;(4)五个连续整数的平均数.
4.指出下列每小题中,两个代数式的意义有什么不同.
(l)![]() 与
与![]() (2)
(2)![]() 与
与![]()
(3)![]() 与
与![]()
5.某校为锻炼学生意志品质,对初一新生进行三天行军训练.第一天行走![]() 千米,第二天比第一天多行走2千米,第三天又比第二天多行走四分之一,则三天共走多少千米?
千米,第二天比第一天多行走2千米,第三天又比第二天多行走四分之一,则三天共走多少千米?
6.一个门框的下部是长方形,上部是半圆形,已知长方形的长为![]() ,宽为
,宽为![]() ,半圆的直径就是长方形的宽,怎样用
,半圆的直径就是长方形的宽,怎样用![]() ,
,![]() 表示该门框的面积和周长?
表示该门框的面积和周长?
7.用字母表示:(1)同分母和异分母分数相加减的运算法则;(2)乘法和加法的运算律;(3)至少写出四个你熟知的图形面积的计算公式.
8.![]() 个球队进行单循环比数列,总的比赛场数是多少?
个球队进行单循环比数列,总的比赛场数是多少?
9.![]() 和
和![]() 是相邻的两个自然数,求
是相邻的两个自然数,求![]() 与
与![]() 的最大公约数与最小公倍数差的平方?
的最大公约数与最小公倍数差的平方?
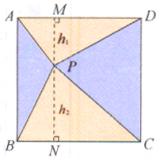
10.如右图,正方形ABCD,P是正方形内的一点,三角形APD的面积是![]() 平方厘米,三角形PBC的面积是
平方厘米,三角形PBC的面积是![]() 平方厘米.求:正方形的面积.
平方厘米.求:正方形的面积.
参考答案:
1.(1)![]() ,(3)
,(3) ![]() ,(5)3,(6)
,(5)3,(6)![]() ,(8)
,(8)![]() 都是代数式;
都是代数式;
(2)![]() ,(4)
,(4)![]() ,(7)
,(7)![]() 都不是代数式.
都不是代数式.
2.(l)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() ;(5)
;(5)![]() ;(6)
;(6)![]() ;(7)
;(7)![]() ;
;
(8)![]() .
.
3.设字母![]() 表示任意一个整数,则
表示任意一个整数,则
(1)所有的奇数可表示为![]() ;
;
(2)所有的偶数可表示为 ![]() ;
;
(3)所有能被 3整除的数可表示为 ![]() ;
;
(4)由于每两个连续整数之间相差1,若没这五个连续整数中中间的一个为![]() ,那么其余4个分别为
,那么其余4个分别为![]() ,
,![]() ,
,![]() ,
,![]() . 因此它们的平均数可表示为
. 因此它们的平均数可表示为
![]() .
.
4.(1)![]() 表示
表示![]() 与
与![]() 的积,
的积,![]() 表示
表示![]() 与
与![]() 的差.
的差.
(2)![]() 表示
表示![]() 与
与![]() 的商,
的商,![]() 表示
表示![]() 与
与![]() 的商的平方. (3)
的商的平方. (3)![]() 表示
表示![]() 与
与![]() 的商,
的商,![]() 表示
表示![]() 除以
除以![]() 的商与
的商与![]() 的和.
的和.
5.![]() 千米
.
千米
.
6.面积为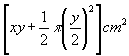 周长为
周长为![]()
7.(1)![]()
![]()
![]() (2)
(2) ![]()
![]()
![]()
![]() (3)
(3)![]()
![]()
8. ![]() (场);9.
(场);9.![]() ;10.
;10.![]() 平方厘
平方厘![]()
![]() 米.
米.
例题分析
例1是用代数式表示几个比较简单的数量关系,这些小学都学过.比较复杂一些的数量关系的代数式表示,课文安排在下一节中专门介绍.
例2是说出一些比较简单的代数式的意义.因为代数式中用字母表示数,所以把字母也看成数,一种特殊的数,就可以像看待原来比较熟悉的数式一样,说出一个代数式所表示的数量关系,只是另外还要考虑乘号可能省略等新规定而已.
重点分析
教科书,介绍了小学用字母表示数的实例,一个是运算律,一个是常用公式,上述两种例子应用广泛,且能很好地体现用字母表示数所具有的简明、普遍的优越性,用字母表示是数学从算术到代数的一大进步,是代数的显著特点。运用算术的方法解决问题,是小学学生的思维方法 ,现在,从具体的数过渡到用字母表示数,渗透了抽象概括的思维方法,在认识上是一个质的飞跃。对代数式的概念课文没有直接给出,而是用实例形象地说明了代数式的概念。对代数式的概念可以从三个方面去理解:
1、从具体的数到用字母表示数,是抽象思维的开始,体现了特殊与一般的辨证关系,用字母表示数具有简明、普遍的优越性.
2、代数式中并不要求数和表示数的字母同时出现,单独的一个数和字母也是代数式.如:2,![]() 都是代数式.
都是代数式.
3、代数式是用基本的运算符号把数、表示数的字母连接而成的式子,一定要弄清一个代数式有几种运算和运算顺序。代数式不含表示关系的符号,如等号、不等号.如![]() ,
,![]() ,等都是代数式,而
,等都是代数式,而![]() ,
,![]() ,
,![]() ,
,![]() 等都不是代数式.
等都不是代数式.
注意事项
1、代数式中数字与字母或者字母与字母相乘时,通常把乘号简写作“·”或省略不写,同时要求数字应写在字母前面.如![]() ,应写作
,应写作![]() 或写作
或写作![]() ,
,![]() 应写作
应写作![]() 或写作
或写作![]() .带分数与字母相乘,应把带分数化成假分数,如
.带分数与字母相乘,应把带分数化成假分数,如![]() 应写成
应写成![]() .数字与数字相乘一般仍用“×”号.
.数字与数字相乘一般仍用“×”号.
2、代数式中有除法运算时,一般按照分数的写法来写.如:![]() 应写作
应写作![]()
3、含有加减运算的代数式需注明单位时,一定要把整个式子括起来.