第8章 多边形
【三维目标要求】
1.了解几种特殊的三角形与多边形的特征,探索、归纳多边形的内角和与外角和公式,并能运用于解决计算。
2.体验探索、归纳过程,学会合情推理的数学思想方法;体验证明的必要性,学会初步说理。
3.欣赏丰富多彩的图案,体验数学美,提高审美情趣。
§8.1 瓷砖的铺设
【教材解读】
瓷砖的铺设是本章教学内容的实际背景,让学生知道铺满地面的图形有的是规则的,有的是不规则的,并了解瓷砖铺设的一般方式。
【重点再现】
1.本节的重点和难点是了解瓷砖如何拼成一块完整的地面和墙面。
2.学习本节的关键是要认真观察,留心生活中的实例。
【难点突破】
课本中本节给出了用正三角形、正方形、长方形、正六边形、不规则的四边形瓷砖铺设的地(墙)面图案。想一想并动手做一做,剪出一些形状、大小都一样的四边形,拼拼看,能否铺满地面而不留空隙?
【知识与生活】
观察自己的家、学校、商店、广场以及大街两旁的人行道上铺设的地砖和墙砖的形状,或到建材市场、或网上查询,收集瓷砖的形状,比一比,看谁收集的多,把你喜欢的几种图案画到下面的方框内。



【同步提升】
【必备功底】 试一试,完成下列题目:
1.瓷砖是生活中常见的装饰材料,你见过那些形状的瓷砖?它们的形状有什么特点?请给以描述。
2.你知道瓷砖能铺满地面的奥秘吗?
【智力拓展】 小小设计家
3.请你设计并绘制两种不同的瓷砖铺设方案,注意讲究美观、大方。
【整合拓展】
4.与你的父母外出旅游时,留心观察各种建筑物的地面、墙面的瓷砖形状及铺设的方法,并绘成草图,展示给同学们并说说你的想法。
【数学趣闻连载】
剪刀和纸片(一)
也许以前你曾这样想过———我以前当然也会这样想———在这世界上,不必要的东西太多了。其实,这是一个错误的观念。表面上似乎无用的东西,从另外一个角度来看,往往又变成很有用的东西。而有些工作上不需要的东西,则可以运用到娱乐方面。
我在整理房间时,看到一堆旧书信和许多细长的纸条,这些纸条是贴壁纸剩余的边脚料,零零碎碎的,乱七八糟。“看样子,这些废纸只有进垃圾箱的命了,都是废物。”我本来有这种想法。无论谁来看,都认为是形同垃圾的废纸。其实,只要巧妙运用,仍有很大的价值。哥哥就准备告诉我,应该怎样利用这些废物。
首先,哥哥要我利用这些纸条。
我拿着约有手掌三倍长的纸条交给哥哥,他说:“你拿着剪刀,把这纸条剪成三部分。”
当我拿起剪刀准备剪时,哥哥又拉住我的手说:“等一下,我的话还没说完,你必须一次就把纸条剪成三部分才可以。”
你说,我该怎么办呢?
8.2三角形
【教材解读】
学习三角形是学习多边形的基础,本节主要要学会:了解三角形的内角、外角及其主要线段(中线、高、角平分线)等概念;会用刻度尺和量角器画出任意三角形的角平分线、中线和高;探索并掌握三角形的外角性质及外角和;理解并掌握三角形的三边关系的性质;了解三角形的稳定性。教学过程中要鼓励学生自主探索,大胆猜想,动手操作,探索发现有关结论,另一方面辅以简单的数学说理,从而确信这一数学结论的正确性。
【重点再现】
本节的重点是三角形的有关概念,三角形的外角的性质及外角和、三角形的三边关系等等。
【难点突破】
三角形外角性质及三角形三边关系性质的应用是本节的难点,学习时要勤于动手,多画图,帮助分析理解,并结合生活实际体会三角形知识的综合运用。
【知识与生活】
有一块三角形形状的优良品种的试验土地,技术人员打算从外地引进四个不同的优良品种进行对比实验,所以现在要把这块土地分成面积相等的四块,请你制定出两种以上的划分方案,以供技术员选择。(可画图说明)
 |  |  |
【同步提升】
【必备功底】
1. 填空
(1)如图,图中以CD为边的三角形共有______个,他们分别是_____________________。
(2)一个三角形中最多有_____个锐角,最少有______个锐角。
(3)如图,图形中是直角三角形的有_______________________________。
(4)已知等腰三角形的一边是6,另一边是5,则第三边是__________;三角形的周长是____________。
(5)三角形的三个内角的比为3:2:5,则三个角分别为______________;三个相邻的外角为________________。
(6)在三角形中相邻的外角是内角的2倍,则此外角的度数是__________。
(7)在△ABC中,∠B和∠C的角平分线交于点O,若∠A=500,则∠AOC=_______。
(8)一个三角形的两边长分别是3cm和8cm,第三边长是奇数,那么第三边长是_______,三角形的周长是_________。


(1) (3)
2.我来判断,用“×”或“√”来表示
(1)三个角都是锐角的三角形是锐角三角形。 ( )
(2)凡等腰三角形都不是直角三角形。 ( )
(3)钝角三角形中有的是等腰三角形。 ( )
(4)一个三角形中最多有一个钝角。 ( )
(5)一个三角形中可以有两个直角。 ( )
(6)等边三角形既不是直角三角形也不是钝角三角形。( )
(7)凡等边三角形都是锐角三角形。 ( )
(8)凡等边三角形都是等腰三角形。 ( )
 3.AD是△ABC的高,AE是△ABC的角平分线,AF是△ABC的中线,自己根据题意画出图形,试写出图中所有相等的角和相等的线段。
3.AD是△ABC的高,AE是△ABC的角平分线,AF是△ABC的中线,自己根据题意画出图形,试写出图中所有相等的角和相等的线段。
【智力拓展】
4.下面有这样一个图形,你能写出图中共有多少个三角形吗?

5.试一试 ,你能否在一个等腰三角形中,放置一个另外一个同样腰长的等腰三角形?画出图形说明。
6.如图,△ABC中,D、E分别是边AC、BC上的中点,你能发现△ABC和△CDE的面积有什么关系吗?

7.等腰△ABC中,AB=AC,周长为16cm,AC边上的中线BD把△ABC分成了周长差为4cm的两个三角形,试求△ABC各边的长。
8.在三角形ABC中,若∠C—∠B=600,∠B—∠A=150,从以上条件中,你能求出∠C的度数吗?试着解答并说明理由。
9.如图,A1,A2,和A3三点,可连成一个三角形;A1,A2,A3,A4四点可连成四个不同的三角形,现在有7个点,即A1,A2,A3,A4,A5,A6,A7,且任意三点都可连成三角形,试问:这7个点最多可连结成多少个不同的三角形?假如是8个点呢?n个点又是怎样的呢?(用含有n的代数式表示)

10.有三条线段a、b、c,当它们满足下列条件时,一定能组成三角形吗?如果不能,请举例说明;如果能,试着说明理由。
(1)a+b>c
(2)a+b>c ; b+c>a
(3)a+b>c ; b+c>a ;c+a>b
11.某市在北边有4个村庄,它们分别恰好位于一个四边形ABCD的四个顶点处,为方便居民用电,市电力局决定,要在4个村庄之间建一个变压器H,以加大供电量,为节约线路,试问,H应建在何处,才能使它到4个村庄的距离和最短?
【整合互动】
12.邀请你的伙伴一起参加,以图中的格点为顶点,能组成多少个直角三角形?用不同颜色的笔画出来,比一比,看谁找的多?
13.和你的父母一起来探究,我们知道:“三角形的内角和为1800。”你能否设计出几种不同的方案,证明出这个性质的正确性呢?(画出图形,简要说明理由),把设计出的方案和你的同学交流一下,看谁的更好。
14.和你们本班的几个同学一起,比一比,看谁说的多?
三角形的稳定性在生活实践中得到了广泛的应用,例如,建筑工人的建筑支架,就是利用了三角形稳定性的道理。实际生活中,还有很多这样的例子,你们能举出多少呢?
想一想,观察一下,四边形具有稳定性吗?你也能举出实例吗?
【数学趣闻连载】
剪刀和纸片(二)
对我来说,这真是一个难题,我只好动脑筋想。哥哥在旁边看着我,似乎也知道我无法解决这个问题。思索再三,我无计可施。“哥哥,你不是开玩笑吧?”我疑惑的问,“这种事怎么可以做到呢!”“你好好动动脑筋……也许你会发现答案。”“我已仔细想过,现在我无法知道怎样做这件事。”“也许你有些地方没弄清楚,还是我来做给你看吧!”
哥哥从我手中接过纸条和剪刀。首先,哥哥将纸条对折,再把纸条从中间剪开,纸条很简单的变成了三部分。
“现在你该懂了吧?”“是呀,不过你怎么可以将纸条对折。”“你自己为什么不对折呢?”
“可是你没有说可以折啊!”“但我也没说不可以折。有问题,你就应该干脆地提出来。”
“你再考我其他的问题,这一次我一定好好想。”
“这里这么多纸条。你能不能让这些纸条的边缘竖立在桌子上,而不是躺在桌子上。”
这一次我不敢大意,经过仔细的思考,我把纸条折成“V”字形,然后放在桌子上。
“你看!,我可以让纸条靠边缘竖立。你没有告诉我不可以对折,所以我这样做。”我得意万分地说。“做的不错》”“还有其他问题考我吗?”我问。
8.3 多边形的内角和与外角和
【教材解读】
本节是三角形有关知识的拓展,学习过程中应使学生探索、归纳多边形的内角和与外角和公式,并能运用于解决计算问题,并从中体验探索、归纳过程,学会合情推理的数学思想方法。
【重点再现】
1. 本节的重点是多边形的内角和、外角和的性质。
2. 本节的难点是这些性质的推出过程的理解。
【难点突破】
填写下表,理解多边形内角和、外角和性质的推导过程。
| 多边形的边数 | 3 | 4 | 5 | 6 | 7 | 8…… | n |
| 分成三角形的个数 | 1 | ||||||
| 多边形的内角和 | 1800 | ||||||
| 多边形的内角与外角的总和 | 3×1800 =5400 | ||||||
| 多边形的外角和 | 3600 |
【知识与生活】
动动手,做一做
有一张五边形纸片,明明一刀把它剪成了一个四边形,龙龙把它剪成了一个五边形,红红一刀把它剪成了一个六边形。自己动手剪一剪,看看他们剪的正确吗?
试着画出剪出的示意图形。
【同步提升】
【必备功底】
1. 填空
(1) 正十边形的内角和等于________每一个内角等于______。
(2)
一个多边形的内角和是外角和的![]() , 则这个多边形是_____边形。
, 则这个多边形是_____边形。
(3) 在四边形ABCD中,∠A=900,∠B:∠C:∠D=1:2:3,则∠B=_______,∠C=_______,∠D=________。
(4) 在一个六边形中,其中四个内角的和是6000,另外两个内角相等,那么这两个内角的度数都是_________。
(5) 如果一个多边形的每一个外角都等于360,那么这个多边形是_______边形。
2. 选择
(1)一个多边形的对角线的条数与边数相等,这个多边形的边数是( )
A 7 B 6 C 5 D 4
(2如果一个多边形中有三个内角相等,其余各角的外角都等于300,则这个多边形的边数不可能是( )
A 4 B 6 C 10 D 15
(3)下列命题中,正确的有( )
① 七边形有14条对角线。②外角和大于内角和的只有三角形。
③若一个多边形的内角和与外角和的比是4:1,则它是九边形。
A 0个 B 1个 C 2个 D 3个
【智力拓展】
3. 已知正n边形每一个内角与其外角的差为900,求内角的度数和边数。
4.一个凸多边形,张明在计算它的内角和,一会儿,张明求得内角和是24000,王刚发现张明在计算过程中少算了一个内角的度数,你能推断一下张明少计算的那个内角的度数吗?这个凸多边形是几边形呢?
5.红红和兰兰在玩剪纸游戏时,剪出来了这样的一个图形,如图,你能求出∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数吗?
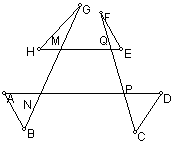
5. 在六边形ABCDEF中,如图,EF∥BC,AF∥DC,∠F=1200,∠A=800,你能算出∠B和∠C的度数吗?并简要说明理由。

【整合互动】
7.探索规律:四边形有2条对角线;五边形有5条对角线;六边形有9条对角线;七边形有14条对角线,那么n边形有多少条对角线呢?
【数学趣闻连载】
剪刀和纸片(三)
“当然!听清楚啊,我用浆糊把纸条的两端粘贴起来,就可以做出长长的纸环。你拿着红色和蓝色的铅笔,沿着纸环的外侧,画一个蓝色的大圆圈,在纸环内侧则画上红线。”
“然后呢?”
“这样就好了。”
我觉得这工作简直太无聊。但我却做不好这简单的工作。本来,我想用蓝铅笔沿着纸环外侧,先画出下道蓝圈,再用红笔画纸环内侧。大概是没注意,我在纸环的两面,都用蓝笔画上了圆圈。因此,我自已也觉得很不好意思。
“你能不能给我另一个纸环?”我停一下又说,“因为我一不小心,就把刚才的纸环画坏了。”
虽然哥哥给我另一个纸环,但我依旧宣告失败。不知道为什么,我在纸环的两面都画了相同的颜色。说真的,我自己也搞不清楚是怎么回事。
“不知道为什么?我明明沿着纸环表面画,没想到又失败了。哥哥,再给我一个纸环好不好?”
“好啊,你尽量拿,这一点纸环,我不会吝啬的。”
读者们猜想结果如何?结果我以在红环的两面画出蓝色,我始终没有使用红笔的机会。这时,我不由双手抱头,开始沉思。
8.4正多边形拼地板
【教材解读】
要使学生通过正多边形拼地板的问题,理解正三角形、正方形、正六边形乃至任意三角形、四边形能镶嵌平面的理由,从中体验应用数学知识解决实际问题的过程,学会必要的数学方法。
【重点再现】
1. 本节的重点是了解可以拼在一起的几何图案。
2. 难点是理解能否拼成几何图形的根据。
【难点突破】
通过本节课的学习,我们知道了,用一种正多边形铺地面时,只有________、________、__________三种能铺满地面,你能说出其中的数学道理吗?
【知识与生活】
走在马路上或是公园的小路上,你有没有发现地上铺的地面砖有的虽然很简单,但却能拼出美丽的图案来?构成图案的每一块地砖都是正多边形吗?你能否自己设计一种正多边形地砖,而且能拼出美丽的图案。
【同步提升】
【必备功底】
1.用一批相同的多边形地面砖来铺满地面,要求各个顶点要聚在一起,且砖与砖之间不留空隙,则下列图形不能选用的是( )
A.正三角形 B.正六边形 C.正方形 D.正十二边形
2.试一试
用几种正多边形拼在一起,也能铺满地面,你能通过生活中的细心观察,举出几个例子吗?画出图形。
【智力拓展】
3. 制作多个同样大小的任意锐角三角形,拼一拼,看它们能铺满地面吗?任意三角形可以吗?把图形画在下面的方框内。
4. 制作多个同样大小的等腰梯形,拼一看它们能铺满地面吗?任意梯形可以吗?把图形画在下面的方框内。
 |  |
(3) (4)
【整合互动】
5.按下列步骤设计图案:
(1) 画一个正方形ABCD;
(2) 去掉两个形状大小一样的直角三角形ABE和DCE;
(3) 将直角三角形ABE和DCE分别放在的位置上直角三角形ADF和DGF处;
(4) 在得到的图形上画出你喜欢的图案;
(5) 再做几个这样的图案,利用它们拼出一个美丽的图案。



【数学趣闻连载】
剪刀和纸片(四)
“这么简单的事情,难道你都不会做吗?”哥哥面露笑容说道,“像这种简单的事情,我马上就可以做到。”
只见哥哥拿着一个新的纸环,好端端地在纸环外侧画上红线,然后递给我看。
因此, 再拿起新的纸环,一面开始画线,一面又小心翼翼,提高警觉,不让这一条移到另一面去。就这样,将纸环旋转一圈,没想到又失败了。我以在纸环两侧都画上同色的线条。我几乎要哭出来,用眼睛偷偷瞄哥哥……只见哥哥露出很狡猾的笑容,在这一刹那,我猜想到失败的理由何在。
“哥哥啊!……你是不是在变魔术?”我正想问。却听见哥哥骄傲地说:“这个纸环有魔力,这是特制的纸环。”
“到底是什么样的纸环啊?外表看起来,和普通的纸环一模一样,难道哥哥装了什么机关吗?”