三角形、 变量之间的关系、 轴对称
一、选择题（每题2分，共24 分）
1、下列图形中，是轴对称图形的有 （ ）个。
①角；②线段；③等腰三角形；④扇形；⑤三角形； ⑥正方形；⑦平行四边形；⑧圆；⑨五边形。
A.5个 B.6个 C. 7个 D.8个
2、 将一张长方形纸片折一次，折痕平分这个长方形的面积，到这样的折纸方法有（ ）
A、1种 B、2种 C、4种 D、无数种
3、国旗是一个国家的象征，观察下面的国旗，是轴对称图形的是 （ ）
A.加拿大、哥斯达黎加、乌拉圭 B.加拿大、瑞典、澳大利亚C.加拿大、瑞典、瑞士D.乌拉圭、瑞典、瑞士
加拿大 哥斯达黎加 澳大利亚 乌拉圭 瑞典
瑞士
4、 下列图案是几种名车的标志，请你指出，在这几个图案中是轴对称图形的共有（ ）
 |
A.4个 B.5个 C. 6个 D.7个
5、小明照镜子的时候，发现T恤上的英文单词
在镜子中呈现“ ＿＿＿＿”的样子，
（A）
（B） （C） （D）
6.小明一出校门先加速行驶，然后匀速行驶一段后，在距家门不远的地方开始减速，而最后停下，
下面哪一副图可以近似地刻画出以上情况：( )
速度
速度
速度
速度
时间 时间 时间 时间
（A） （B） （C） （D ）
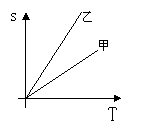
7、某人骑车外出，所行的路程（千米）与时间（小时）的关系如图所示，现有下列四种说法：
①第3小时的速度比第1小时中的速度快；②第3小时的速度比第1小时中的速度慢；③第3
小时后已停止前进；④第3小时后保持匀速前进。其中说法正确的是（ ）
（A）②、③ (B) ①、③ (C) ①、④ (D) ②、④
( 8)
（9）
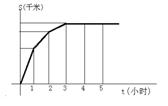
8、如上图，
于D，
于E，
于F，
于A，则
中，AC边上的高为（ ） A、AD B、GA C、BE D、CF
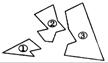9、如图，射线甲、乙分别表示甲、乙两车所走路程
与时间的关系图，则两车速度关系是：( )
A 、 甲比乙快 ； B 、乙比甲快 ；
C 、 甲乙同速 ； D 、不能判断。 （10）
10、如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃
店去配一块完全一样的玻璃，那么最省事的办法是（ ）（A）带①去 （B）带②去
（C）带③去 （D）带①和②去
11、小颖从家到学校是1000米，她以不变的速度从家出发
20.分钟到书店看了10分钟的书，接着她加快步伐匀速行走，用10分钟到了学校，下列图象中表示
小颖从家到学校的时间（分）与路程（米）之间的关系是（ ）
12、甲乙两同学约定游戏规则:甲先骑自行车到终点后跑步回起点，而乙则跑步到终点后骑自行车回起点，两人同时出发，最后两人同时回到起点。已知甲骑自行车速度比乙骑自行车速度快，若
某人离开起点的距离与所用时间的关系可用图象表示，则下列选项正确的是（ ）
 |
（1） （2） （3） （4）
A、甲是图（1），乙是图（2）；
B、甲是图（3），乙是图（2）；
C、甲是图（1），乙是图（4）； D 、甲是图（3），乙是图（4）；
二．填空题。(每题 2分，共 26分)
1.有六根细木棒，它们的长分别是2,4,6，8,10,（单位：cm），能搭成三角形的三根细
木棒的长分别是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
2、在日常生活中，事物所呈现的对称性能给人们以平衡与和谐的美感. 我们的汉字也有类
似的情况，呈现轴对称图形的汉字有 （请举出两个例子）.
3、等腰三角形的腰长是6，则底边长a的取值范围是______________________。
4、等腰三角形一个底角为50°，则此等腰三角形顶角为________________________。
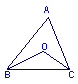5、如图，△ABC中，∠ABC和∠ACB的平分线交于点O，若∠BOC=120°, 则∠A=________°
5 6 9 10
6、如图, 一圆锥高为6cm，当底面半径从5cm变化到10cm时, 体积从 变化到 (保留π)
7、某下岗职工购进一批苹果，到集贸市场零售，已知卖出的苹果数x与y的关系如下表
| 数量x（千克） | 1 | 2 | 3 | 4 | 5 |
| 售价y（元） | 2＋0.1 | 4＋0.2 | 6+0.3 | 8+0.4 | 10+0.5 |
写出用x表示y的关系式是＿＿＿＿＿。
8、观察下列各式: 1+1×3 = 22, 1+2×4 = 32, 1+3×5 = 42,……
请将你找出的规律用公式表示出来: .
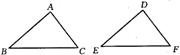
9.如图，在△ABC和△DEF中，已知AB=DE，要使△ABC≌△DEF，根据三角形全等的判定定理，还需
添加条件（填上你认为正确的两种情况）_______________________________．
10、如图，镜子里号码如图，则实际纸上的号码是_________________。
11、如图，已知DE是AC的垂直平分线，AB=10cm，BC=11cm，则ΔABD的周长为＿＿＿＿cm。
 |
12、如图，∠A=20
，∠C=40
，∠ADB=80，则∠DBC=＿＿＿，图中共有等腰三角形＿＿＿个。
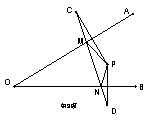
13、如图，点P关于OA、OB的对称点分别为C、D，连结CD，交OA于M，交OB于N，若
PMN的周长=8厘米，
| |
三、看图说话。(4分)
是小兵骑自行车回家的速度与时间的关系，你能想象出他回家路上的情景吗？请写一个简单的故事来描述小兵在这段时间内的活动情况，在你的故事中，描述小兵在不同时间里都做了什么事情。
四、（4分）在下面过程中的横线上填空，并在括号内注明理由。
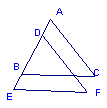
已知：如图BC∥EF，BC=EF，AB=DE；说明ＡＣ与ＥＦ相等。
解：∵BC∥EF（已知）
∴∠ABC=∠__________（ ）
在△ABC和△DEF中
______=_______
(五. 1)
∵ _______=________
______=________
∴△ABC≌___________ ( )
∴ _______=__________ ( )
五．证明题。（每题5分，共25分）
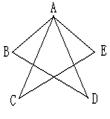
1、已知：AB = AE，AC = AD， 要使EC = BD需附加一个什么条件？说明理由。
2．已知：如图，BD＝CD，∠ABD＝∠ACD，DE、DF分别垂直于AB及AC交延长线于E、F．
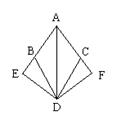求证：DE＝DF
2、已知：如图，
于点
于点F，且
BE=DF, 求证：AB∥DC
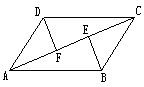
4、已知：如图，AD平分∠BAC,DE⊥AB,DF⊥AC，DB=DC，
求证：△ABC是等腰三角形。
| |
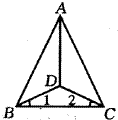
求证： AＤ⊥BC．（用两种方法）
| |
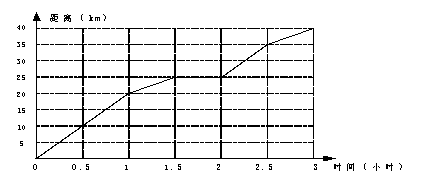
1、 如图反映了小强骑自行车在两城镇间旅行的时间（小时）（））与距离（km）的变化关系，
已知两城镇间的距离为40km，根据这个图象，你能得到关于小强在这一旅途中的哪些信息
（至少写4条信息）（4分）
2、利用轴对称图形设计一个美丽的图案，并说明你要表达的意义。（4分）
3、 某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和书包的单价之和是452元，且随身听的单价比书包单价的4倍少8元。（5分）
（1）该同学看中的随身听和书包的单价各是多少元？
（2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物劵30元销售（不足100元不返劵，购物劵全场通用），但他只带来400元钱，如果他只在一家超市购买看中的这两种物品，你能说明他可以选择哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？