第一章测试卷A卷
一、选择题（每题3分，共30分）
1. 图中三角形的个数是（ ）
A. 3个 B. 4个 C. 5个 D. 6个
2. 下列各组数中不可能是一个三角形的边长的是（ ）
A. 5，12，13 B. 5，7，7
C. 5，7，12 D. 101，102，103
3. 已知一个三角形两个锐角的差为10°，则这两个锐角的度数（ ）
A. 不能确定 B. 分别是60°，50°
C. 分别是55°，45° D. 分别是50°，40°
4. 已知一个三角形的三条高的交点不在这个三角形的内部，则这个三角形（ ）
A. 必定是钝角三角形 B. 必定是直角三角形
C. 必定是锐角三角形 D. 不可能是锐角三角形
5. 下列说法正确的是（ ）
A. 有一个外角是钝角的三角形必定是锐角三角形
B. 三条线段a，b，c，若满足a>b>c，且a<b+c，则这三条线段必能组成一个
三角形
C. 有两个角和一条边彼此相等的两个三角形全等
D. 有两条边和一个角对应相等的两个三角形全等
6. 下列说法正确的是（ ）
A. 两个周长相等的长方形全等
B. 两个周长相等的三角形全等
C. 两个面积相等的长方形全等
D. 两个周长相等的圆全等
7. 如图，∠1=∠2，AB=CD，AC与BD相交于点O，则
图中必定全等的三角形有（ ）
A. 2对 B. 3对
C. 4对 D. 6对
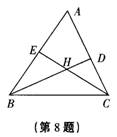
8. 如图，在△ABC中，高线BD，CE相交于点H，若∠A
=60°，则∠BHC的度数是（ ）
A.60° B. 90° C. 120° D. 150°
9. 要测量河两岸相对的两点A，B的距离，先在AB的垂线BF
上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，
C，E在一条直线上（如图所示），可以说明△EDC≌△ABC，
得ED=AB，因此测得ED的长就是AB的长，判定△EDC≌△ABC最恰当的理由是（ ）
A. 边角边 B. 角边角 C. 边边边 D. 边边角
10. △ABC和△AˊBˊCˊ中，条件①AB= AˊBˊ；②BC= BˊCˊ；③AC= AˊCˊ；④∠A=∠Aˊ；⑤∠B=∠Bˊ；⑥∠C=∠Cˊ。则下列各组条件中不能保证△ABC≌△AˊBˊCˊ的是（ ）
A. ①②③ B. ①②⑤ C. ①③⑤ D. ②⑤⑥
二、填空题（每小题3分，共30分）
11. 在△ABC中，已知∠A=30°，∠B=70°，则∠C的度数是 。
12. 在Rt△ABC中，一个锐角为25°，则另一个锐角为 度。
13. 已知一个三角形的三条边长为2，x，7，则x的取值范围是 。
14. 如图，CD是Rt△ABC斜边上的高，与∠A相等的角是 ，理由是 。
15. 如图，AD是△ABC的中线，△ABC的面积为100㎝2，则△ABD的面积是
㎝2。
16. 如图AD，CE是△ABC的角平分线，它们相交于点P，已知∠B的度数为
，
则∠APE的度数是 。
17. 如图，AD，CE是△ABC的两条高，它们相交于点P，已知∠BAC的度数为，
∠BCA的度数为
，则∠APC的度数是 。
18. 如图，AD平分∠BAC，AC=AB，则△ABD≌△ACD。理由是
AC=AB（已知）
∠CAD=∠BAD（
） △ABD≌△ACD（SAS）。
= （ ）
19. 要画出∠AOB的平分线，分别在OA，OB上截取OC=OD，
OE=OF，连结CF，DE，交于P点，那么∠AOB的平分线
就是射线OP，要说明这个结论成立，可先说明△EOD≌
△ . 理由是 ，得到∠OED=∠ ，再说明△PEC≌△ ，理由是 ，得到PE= ；最后说明△EOP≌△ ，理由是 ，从而说明了∠AOP=∠BOP，即OP平分∠AOB。
20. 如图，在△ABD和△ACE中，有下列四个论断：（1）
AB=AC；（2）AD=AE；（3）∠B=∠C；（4）BD=CE。
请以其中三个论断作为条件余下一个论断作为结论，
写出一个真命题（用序号××× ×的形式写出。
能写出几个就写几个）
三、作图题（6分，要求写出作法）
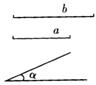
21. 如图，已知线段a，b，∠。画△ABC，使其中有一个内角等于∠，且∠的
对边等于a，另外一边等于b。
四、解答题（共54分）
22. （8分）有四根长度分别为10厘米，12厘米，15厘米，25厘米的铁丝，从中取三根搭三角形，试写出所有的选取方法。
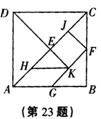
23. （8分）找出七巧板中（如图）全等的图形。
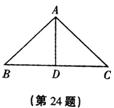24. （8分）如图，AD是△ABC的高，且AD平分∠BAC，
请指出∠B与∠C的关系，并说明理由。
25. （10分）已知两个三角形有两条边和其中一条边上的高对应相等，那么这两个三角形全等。请说明理由（填空）。
解：如图，在△ABC和△AˊBˊCˊ中，已
知AB= AˊBˊ，BC= BˊCˊ，AD⊥
BC于D，AˊDˊ⊥BˊCˊ于Dˊ，且
AD= AˊDˊ。
AB= AˊBˊ
Rt△ ≌ Rt△ ∠ =∠ .
AD= AˊDˊ
AB= AˊBˊ
= △ABC≌△AˊBˊCˊ( )
=
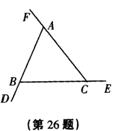
26. （10分）如图，D，E，F是△ABC的三边延长线上的点，
用量角器量出∠FAB，∠DBC，∠ECA的度数，计算出
∠FAB+∠DBC+∠ECA的结果，并说明结果是否正确？
27. （10分）阅读理解：
某校二（1）班学生到野外活动，
为测量一池塘两端A，B的距离，
设计出如下几种方案：
（Ⅰ）如图先在平地取一个可直
接到达A，B的点C，再连接AC，
BC，并分别延长AC至D，BC
至E，使DC=AC，EC=BC，最
后测出DE的距离即为AB之长。
（Ⅱ）如图（2），先过点B作AB的垂线BF，再在BF上取C，D两点，使BC=CD，接着过点D作BD的垂线DE，交AC的延长线于点E，则测出了DE的长即为A，B的距离。
阅读后回答下列问题：（1）方案（Ⅰ）是否可行，理由是 。
（2）方案（Ⅱ）是否可行，理由是 。
（3）方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是 ，若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？