初二级第一学月数学试题

初二级第一学月数学试题　　

　　　　　　　　

　　　

时间：120分钟　 　　　总分：150分

一、精心选一选(（本大题共10小题，每小题4分，满分40分)

1、下列不等式中，是一元一次不等式的是　　　　　　　　　　　　　  （　　　）

　A、　　　 B、　　　　C、　　　　D、

2、下列命题：①若，则；②若，则；③若，则；④；⑤若，则。其中正确的有　　（　　　）

　A、1个　　　　  B、2个　　　　  C、3个　　　　　 D、4个

3、下列从左到右的变形中，是分解因式的有　　　　　　　　　　　　　 （　　　）

　①②③ ④　⑤

　A、1个　　　　  B、2个　　　　  C、3个　　　　　 D、4个

4、不等式的非负整数解的个数是　　　　　　　　　　　  （　　　）

　A、5个　　　　  B、4个　　　　  C、3个　　　　　 D、2个

5、用分组分解法分解因式时，正确的分组方法是　　　 （　　　）

　A、　　　　　 　 B、

C、　　　　　　  D、

6、若不等式的解集是，则a、b应满足的条件是　　　　  （　　　）

　A、且　　 B、且　　C、且　　 D、且

7、已知实数x、y同时满足三个条件：①；②；

③。则实数p的取值范围是　　　　　　　　　　　　　　　  （　　　）　　　　　　　　　　　　　　　　　　　　　　

　A、　　　　 B、　　　　 C、　　　　  D、

8、若0<a<1,则下列四个不等式中正确的是　　　　　　  　　　（　　　）

　A、　　　　B、　　 C、　　　D、

9、某商品的进价为1000元，出售的标价为1500元。商店为减少库存，要求以利润率不低于15%的售价打折出售，则售货员在卖出此种商品时最多可优惠（　　 ）　　　　　　　 

　A、50元　　　 B、150元　 　　C、250元　　　 D、350元

10、若二次三项式可分解为，则的值是　　 （　　 ）

　A、　　　　  B、1　　　　 C、　　　　  D、2

二、细心填一填(本大题共10小题，每小题3分，满分30分)

11、当x　　　 　 时，对一次函数有y＞0。

12、观察图形，根据图形面积的关系，不需要连其他的线，便可

以得到一个用来分解因式的公式，这个公式是 　　　　 ；

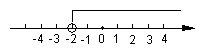13、已知关于x的不等式的解集如图

所示，则m的值为　　　　  。

14、若是的一个因式，则c=　　　　　  。

15、若一次函数的图象不经过第四象限，则k满足的条件为　　　　　　　 。

16、多项式9a²+1加上一个单项式后，使它能成为一个整式的完全平方，则加上的一个单项式可以是_______________________。（填上一个你认为正确的答案即可）

17、若不等式组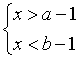有解，则不等式组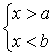的解集是　　　　　　　　 。

18、若，则的值是　　　　　　　 。

　　　　　　　  a　 b　　　　　　　  x　4

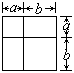
19、定义一种新算法　　　　 =ad-bc则满足　　　  <-2的x的取值范围是

　　　　　　　　　  c　 d　　　　　　　  3　2

______________。

20、在日常生活中，如取款、上网等都需要密码，有一种用“分解因式”结果产生的密码，方便记忆。原理是：如对于多项式，因式分解的结果是，若取x=9，y=9，则各个因式的值是：，于是就可以把“018162”作为一个六位数的密码。对于多项式，取x=10，y=10时，用上述方法产生的密码是　　　　　　　　　　

　（写出一个即可）

三、耐心做一做：(本大题共8题，共80分)

21、解下列不等式（组），并把解集表示在数轴上。（每题5分，共10分）

 ⑴、　　　　　　　　　  ⑵、

22、把下列各式分解因式。（每题4分，共20分）

　⑴、 　　　　　　　　　　⑵、

⑶、ac-bc-a^2-b²　　　　　　　　　　　　　　　 ⑷、

(5)

23、利用分解因式计算（每题5分，共10分）

(1)  (-2)²⁰⁰⁸-(-2)²⁰⁰⁷

(2)目前家庭用1KW.h电0.46元，团团家1月用电109KW.h,2月份用电112 KW.h，

3月份用电79KW.h，那么团团家第一季度需交电费多少元？(1KW.h=1度)

24、(本题6分)重庆市一山区学校为部份家远的学生安排住宿，将部份教室改造成若干间住房。如果每间住5人，那么有12人安排不下；如果每间住8人，那么有一间房还余一些床位。那么该校可能有几间住房可以安排学生住宿？住宿的学生可能有多少人？

25、(本题7分)利用分解因式解方程：(x－4)－(4－x)(8－x)=12

26、(本题7分)已知，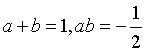

(1)求(a-b)²值；(3分)

(3)求a(a+b)(a-b)-a(a+b)²的值。(4分)

 

27、(本题10分)圆圆影碟出租店开设两种租碟方式：一种是零星租碟，每张收费1元；另一种是会员卡租碟，办卡费每月15元，租碟费每张0.4元 . 小彬经常来该店租碟，若每月租碟数量为x张.

(1)写出零星租碟方式应付金额y1(元)与租碟数量x（张）之间的函数关系式；（3分）

(2)写出会员卡租碟方式应付金额y2(元 )与租碟数量x(张)之间的函数关系式；（3分）

(3)小彬选取哪种租碟方式更合算？（4分）

28、(本题10分)2006年3月11日中国足球超级联赛拉开了序幕。“重庆力帆”队再次出现在联赛中，力帆俱乐部根据足协的记分规则制定了相应的奖励方案如下表：

	胜一场	平一场	负一场
积分	3	1	0
奖金（元/人）	1500	700	0

　力帆俱乐部要求足球队进行到第12轮结束时应记分19分。

　⑴、请通过计算为力帆足球队设计出胜、平、负的场次以满足俱乐部要求；(6分)

　⑵、若每赛一场，每名参赛队员均得出场费500元，设该队其中一名参赛队员所得奖金与出场费的和为W（元），试求W的最大值。(4分)

　　　　　　　　　　　　　　　　　　　　　　　　　　　

初二级第一学月数学试题

参考答案

一、精心选一选(（本大题共10小题，每小题4分，满分40分)

1、D；  2、B；　3、B；　4、B；　5、C；　6、C；　7、D；　8、A；　9、D；　10、A

二、细心填一填(本大题共10小题，每小题3分，满分30分)

11、　　  12、　　 13、　　  14、4　　　　15、　　  16、±6a,-1,-9a² , 　17、　18、4或　 19、x<5　　20、103010（301010、101030）

三、耐心做一做：(本大题共8题，共80分)

21、⑴　

 ⑵由不等式①得：；由不等式②得：∴不等式组的解集为：

22、⑴　　　　　 ⑵

⑶ (a-b)(a+b+c)　　　　　　　　　 ⑷ (m-5)(m+2)　　  (5)5(x-y)²(a-2x+2y)

23、解：(1)

　　　　(2)0.46×109+0.46×112+0.46×79=0.46×(109+112+79)= 0.46×300=138(元)

　　　　答：团团家第一季度需交电费138元。

24、解：设学校有x间住房可以安排学生住宿，则

0<5x+12-8(x-1)<8

0<-3x+20<8

-20<-3x<-12

　 ∵x不整数　　∴x=5或6

当x=5时,学生有37人

当x=6时,学生有42人

答：学校有5间或6间住房可以安排学生住宿，对应的学生有37人或42人。

25、解：x=7

26、解：(1)(a-b)²=(a+b)²-4ab=12-4×()=3

　　　　(2)原式=a(a+b)(a-b-a-b)

=-2ab(a+b)

=-2 ()×1

=1

27、解：22.（1）　　　　　 （2）

（3） 当x＞25时，选择会员卡方式合算

当x=25时，两种方式一样

当x＜25时，选择零星租碟方式合算

28、解：设胜x场、平y场，则负场，由已知得：

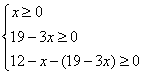　　　 　　　　　即

　　　　  ∵

　　　　  ∴　　 即

　　　　  ∴

　　　　  又∵x为整数　　　　  ∴x=4、5、6

	胜（场）	平（场）	负（场）
方案一	4	7	1
方案二	5	4	3
方案三	6	1	5

　　　　 ∴有以下三种方案：

　　　　  ⑵

　　　　　　　  

　　　　　　 ∵　　 ∴x越小，W的值也越大

　　　　　　 ∴当时，W有最大值，（元）

　　　　　  答：W的最大值为16800元。