初二数学阶段检测试卷（2004.9.25）
一、填空题（每题2分，共32分）
1、
的相反数是
，
的绝对值是
.
2、计算：
=
，
.
3、化简：
，
.
4、
=
，
.
5、计算：
，
.
6、若
；若
.
7、
的平方根是
；
的立方根是
.
8、若
；若
则x=
.
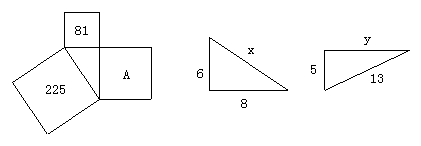9、图中字母A代表正方形的面积，则正方形A的面积是
.
（第9题） （第10题）
10、如图：三角形都是直角三角形，则x= ，y= .
11、当x
时，
有意义；当x
时，
有意义.
12、若x-12是225的算术平方根，则-x的立方根是 .
13、木工做一个长方形的桌面，量得桌面的长为60cm，宽为32cm，对角线长为68cm，这个桌面 （填“合格”或“不合格”）
14、有一个长为12Cm，宽为4cm，高为3cm的长方体铁盒，在其内部要放一根笔直的铁丝，则这根铁丝最长是 .
15、正方形的面积为18cm2，则一条对角线长为 cm..
16、计算器探索：若
（n为正整数），则n至少为
.
二、选择题（每题2分，共20分）
1、实数
的大小关系是…………………………………………………………（ ）
（A）
（B）
（C）
（D）
2、下列计算结果正确的是…………………………………………………………………（ ）
（A）
（B）
（C）
（D）
3、在实数
中无理数的个数有…………………（ ）
（A）2个 （B）3个 （C）4个 （D）5个
4、
的平方根是………………………………………………………………………（ ）
（A）36 （B）-36 （C）±36 （D）±6
5、如果线段a、b、c能构成直角三角形，则a:b:c可能是………………………………（ ）
（A）1:2:3 （B）1:3:5
（C）3:4:6
（D）5:
6、直角三角形两直角边长分别为7，24，则斜边上的高为………………………………（ ）
（A）7
（B）24
（C）
（D）
7、等腰三角形腰长为10，底边上长为12，则此三角形的面积为………………………（ ）
（A）48 （B）60 （C）960 （D）120
8、若a为实数，则下列式子中正确的是…………………………………………………（ ）
（A）
（B）
（C）
（D）
9、△ABC中，∠A，∠B，∠C的对边依次为a，b，c，且a2:b2:c2=1:1:2，则△ABC的形状是…………………………………………………………………………………………（ ）
（A）等腰三角形 （B）直角三角形 （C）等腰直角三角形 （D）等边三角形
10、实数a在数轴上的位置如图所示，下列式子①a，②-a，③-a2，④a2，⑤a3，⑥
中存在平方根的有……………………………………………………………………………（ ）
（A）2个
（B）3个
（C）4个 （D）5个
三、计算题（每题4分，共24分）
1、
2、
3、
4、
5、
6、用计算器计算：
（保留三个有效数字）
四、在数轴上画出
和
表示的点.（4分）
五、解答题（共20分）
1、 （5分）长方形的面积为12cm2，对角线长为6cm，求长方形的周长.
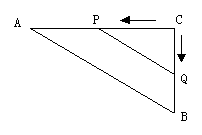
2、（8分）△ABC中，AB=50cm，AC=40cm，∠C=90°，点P从点C开始沿CA边向点A以4cm/s的速度移动，同时另一点Q由C点开始以3cm/s的速度沿着CB边移动.
问：（1）几秒钟后PQ的长为
cm.
（2）几秒钟后，△PCQ的面积等于△ABC的面积的
3、探索与创新题（7分）
观察下列各式以及验证过程：
（1）
验证：
.
（2）
验证：
.
（1）按照上述两个等式以及验证过程的基本思路，猜想
的变形结果，并进行验证；
（2）针对上述各式反映的规律，写出用n（n≥2的整数）表示的等式，并说明理由.