初二数学第二学期期末质量抽查试卷

初二数学第二学期期末质量抽查试卷

（满分：100分　 完卷时间：90分钟） 　　　　　　　

题号	一	二	三	四	五	六	总分
得分

一、　　　　　  填空题（每小题2分，共30分）

1．　若直线过点（0，3），则b=________.

2．　若一次函数中，y随x的增大而减小，则k的取值范围是________.

3．　方程的解为________.

4．　若方程的两实数根是α和β，则α²+β²=________________.

5．　将抛物线沿x轴向左平移2个单位后所得抛物线的解析式是_________.

6．　若抛物线与x轴有两个不同的交点，则k的取值范围是___________.

7．　关于x的方程的解为_____________.

8．　某地的电话月租费（不含通话费）25元，通话费每分钟0.15元，则每月话费（月租费与通话费的和）（元）与通话时间（分钟）之间的关系式是　　　　　　　　 ____.

9．　请写出一个开口向下，且图象在y轴上的截距为3的二次函数解析式：_____________.

10．　　　　　　  平面上到A、B两点距离相等的点的轨迹是___________________________.

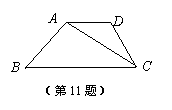
11．　　　　　　  如图，梯形ABCD中，AD//BC，AD=3cm，BC=9cm，那么_________.

12．　　　　　　  梯形的中位线长8cm，高10cm，则该梯形的面积为_________ cm².

13．　　　　　　  已知菱形的周长是24cm，一条较小的对角线的长是6cm，则该菱形较大的内角是_______度.

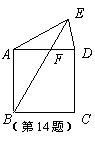
14．　　　　　　  如图,E为正方形ABCD外一点,AE=AD,BE交AD于F,∠ADE=75⁰，则∠AFB=______度.

15．　　　　　　  如图，在Rt△ABC中，∠BAC=90⁰，点M为斜边BC的中点，AM=5cm，∠AMC=45⁰，将△AMC沿AM翻折，点C落在△ABC所在平面内的C^/处，那么BC^/ 的长为_____ cm.

二、　　　　　  选择题（每小题2分，共8分）(每题的四个选项中只有一个正确)

16．下列方程中实根存在且两实数根之和为1的是 …………………………………（　　  ）

（A）；（B）；（C）；（D）

17．如果函数的图象经过第一、二、四象限，那么函数的大致图象是（　　  ）

（A）　　　　　　　　　　　　　　 （B）　　　　　　　  　　 （C）　　　　　  （D）

18．以下几种图形①等腰三角形，②矩形，③菱形，④正方形，⑤等腰梯形，⑥圆中，既是轴对称图形又是中心对称图形的有 ………………………………………………（　　　）

（A）2种；　　　（B）3种；　　　　 （C）4种；　　　　 （D）5种

19．“求作△ABC，使∠A=30⁰，AB=4，BC=5”，你认为…………………………（　　　）

（A）不能作出符合条件的三角形；　　  （B）能作出这样的三角形，且大小形状唯一确定；

（C）能作出两个既符合条件又不重合的三角形；（D）可以作出许多个符合条件又不重合的三角形；

三、 （每小题6分，共30分）

20．解方程：　　　

21．已知关于的方程的一个根是-2，求m的值和它的另一个根。

22．已知关于的方程有两个相等的实数根，求 k的值。

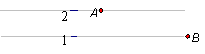
23．如图，已知某校操场内两点A、B的坐标分别为（1，2）、（4，1），王老师在跑道（轴）上行走。

y

（1）王老师到什么位置时离A点最近？直接写出此点的坐标。

（2）王老师到什么位置时，到A、B两点的距离相等？

请求出此点的坐标。（写出计算过程）

24．如图，在四边形ABCD中，AB=1，BC=5，CD=4，AD=，且AB⊥AD。

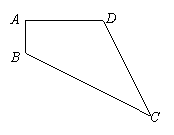求四边形ABCD的面积；

-

四、（本题每小题7分，共14分）

25．如图，平行四边形ABCD中，相邻两边之差为2，对角线AC=6，且AC⊥AB。

求平行四边形ABCD的周长。

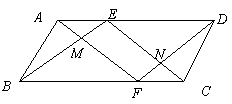26．如图，平行四边形ABCD中，E、F分别为边AD、BC上的点，且AE=CF，连结AF、EC、BE、DF，AF与BE交于M，EC与DF 交于N。

求证：MFNE是平行四边形　

　　　　　　　　　　　　　　　　　　　　　 　　　　　　　 

 

五、（本题8分）

27． 一次函数的图象分别交x轴、y轴于A、B两点，某二次函数的图象也经过A、B两点，且二次项系数为1.

（1）　　　 求该二次函数的解析式；

（2）　如果将该二次函数图象与x轴另一交点记作C，点D为二次函数图象的顶点，那么直线CD与AB是否平行？请说明理由

六、（本题10分）

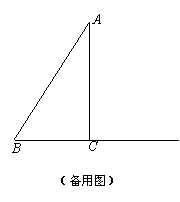
28．Rt△ABC中，∠C=90⁰，∠A=30⁰，AB=4，将一个30⁰角的顶点P放在AB边上滑动，保持30⁰角的一边平行于BC，且交边AC于点E，30⁰角的另一边交射线BC于点D，连ED。

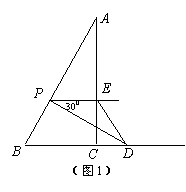（1）如图1，当四边形PBDE为等腰梯形时，求AP的长；

（2）四边形PBDE有可能为平行四边形吗？若可能，求出

PBDE为平行四边形时AP的长；若不可能，说明理由；

（3）若点D在BC边上（不与B、C重合），试写出线段AP

的取值范围。

杨浦区2005学年度第二学期初二数学试卷答案及评分标准2006.6

一、填空

1．3，2．k＜-1，3。，4。8，5。，6。k＜4，7。，

8． ，9。略，10。线段AB的垂直平分线，11。，12。80，13。120，

14。60，15。

二、择题（每小题2分，共8分）(每题的四个选项中只有一个正确)

16．A ，17。D，18。C，19。B

三、 （每小题6分，共30分）

20．解：整理原方程得 ----------------------------------------------2分

　 ∴------------------------------------------------------------------------2分

　 ∴-----------------------------------------------------------------------------------2分

或：整理原方程得 ----------------------------------------------------------------2分

∴-------------------------------------------------------------------------------2分

∴-----------------------------------------------------------------------------------2分

21．解：法一：∵一个根是-2，∴，------------------------------2分

　　　　  ∴------------------------------------------------------------------------------------2分

　　　　  解方程得另一根为---------------------------------------------2分

法二：设另一根为a，则a·（-2）=----------------------------------------------------------------1分

　　　∴a= ------------------------------------------------------------------------------------------2分

　　　∵a+（-2）=，即------------------------------------------------------------1分

　　　∴  ---------------------------------------------------------------------------------------2分

22．解：∵方程有两个相等的实数根，　

　　∴△=------------------------------------------------------------------2分，1分

即 ---------------------------------------------------------------------------------1分

　　∴ k₁=4，k₂= -2  ------------------------------------------------------------------------------------2分

23． 解；（1）此点的坐标（1，0）------------------------------------------------------------------2分

　 （2）设此点坐标为P（x，0）--------------------------------------------------------------------1分

　　则PA²=PB²，即（x-1）²+4=（x-4）²+1--------------------------------------------------------1分

　　则x=2，即P（2，0）-----------------------------------------------------------------------------2分

24．

解：连BD， ∵AB⊥AD，AB=1，AD=，∴BD= ---------------2分

又∵BC=5，CD=4，∵3²+4²=5²∴BD²+ CD²=BC²，

∴△BDC为直角三角形，且BD⊥DC， ------------------------------------------------------------2分

∴四边形ABCD的面积=-----------------------------------2分

四、（本题每小题7分，共14分）

25．

解：∵相邻两边之差为2，且AC⊥AB，∴设AB=x，BC=x+2 -------------------------------1分

∵AC⊥AB，∴△ABC为 Rt△， ∴AB²+AC²=BC²， 即x²+36=（x+2）²-----------------1分

∴x=8，即AB=8，BC=10-------------------------------------------------------------------------------2分

∵ABCD是平行四边形，∴AB=CD，AD=BC -----------------------------------------------------1分

∴ABCD的周长=（AB+BC）×2=（8+10）×2=36-----------------------------------------------2分

26．　　　　　　　　　　　　　　　　　　　　　 　　　　　　　 

证明：∵ABCD是平行四边形，∴AD//BC，即AE//CF， --------------------------------------1分

∵AE=CF，∴AECF是平行四边形，------------------------------------------------------------------1分

∴EC//AF即EN//MF--------------------------------------------------------------------------------------1分

∵ABCD是平行四边形，∴AD//BC，且AD=BC，∴DE//BF，且DE=BF-------------------1分

∴BEDF是平行四边形，---------------------------------------------------------------------------------1分

∴BE//DF即EM//NF--------------------------------------------------------------------------------------1分

∴MFNE是平行四边形-----------------------------------------------------------------------------------1分

五、

27．解：（1）由题意得A（-3，0），B（0，3）--------------------------------------------1分，1分

设二次函数的解析式为y=x²+bx+c，则c=3，b=4--------------------------------------------------2分

∴二次函数的解析式为y=x²+4x+3

（2）平行----------------------------------------------------------------------------------------------------1分

由题意得C（-1，0），D（-2，-1）------------------------------------------------------------1分，1分

设直线DC的解析式为y=kx+b

则，解得，----------------------------------------------------------------------1分

 ∴直线DC平行于直线

六、28．

解：法一：（1）∵∠C=90⁰，∠A=30⁰，∴∠B=60⁰，

∵PBDE为等腰梯形且PE//BD，∴PB=ED，∠BDE=∠B=60⁰，∠BDP=∠DPE=30⁰，---2分

∴∠EDP=30⁰，∴PE=ED=PB---------------------------------------------------------------------------1分

设PE=x，则ED=PB=x，且AP=2x

由AP+PB=AB得3x=4，---------------------------------------------------------------------------------1分

∴x=，即AP=----------------------------------------------------------------------------------------1分

法二：（1）设AP=x，则BP=4-x

∵∠C=90⁰，∠A=30⁰，∴∠B=60⁰，

∵PE//BC，∴∠B+∠BPE=180⁰，∵∠EPD=30⁰，∴∠BPD=90⁰，-----------------------------1分

在Rt△ABC中，∵∠C=90⁰，∠A=30⁰，AB=4，∴BC=2 ---------------------------------------1分

在Rt△BPD中，∵∠BPD=90⁰，∠B=60⁰，BP=4-x，∴BD=8-2x-------------------------------1分

∴CD=6-2x，∵PBDE为等腰梯形，∴ED=BP=4-x，∠EDB=∠B=60⁰，

∴2CD=ED，即12-4x=4-x，-----------------------------------------------------------------------------1分

∴x=，即AP= ---------------------------------------------------------------------------------------1分

（2）可能----------------------------------------------------------------------------------------------------1分

∵PE//BC，∴当PE=BD时PBDE为平行四边形，

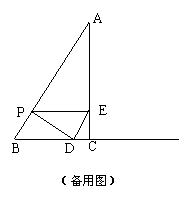此时点D在线段BC上

∴设AP=x，则BP=4-x，BD=8-2x，CD=2-BD=2x-6，ED=BP=4-x，

∵∠EDC=∠B=60⁰，∴2CD=ED，即4x-12 = 4-x

∴x=，即AP=-------------------------------------------------2分

（3）3＜AP＜4--------------------------------------------------------2分