初二第一学期第一次月考试卷

岔河镇2004—2005学年度第一学期

初二第一次月考试卷

时间100分钟,满分100分,命题人:岔南初中数学组

学校_________班级________姓名________得分______

一、填空题（本题共13小题，每小题2分，共26分）

1、多项式a²-4b²,a²+4ab+4b²,a²-2ab-8b²的公因式是_________________。

2、计算：37×101²-99²×37=______________。

3、若x²-8x+k=(x-2)(x-6)，则k=_____________。

4、分解因式：- m²- n²+2mn+1=__________________。

5、若a²+4ab+5b²-2b+1=0，则a+b=_________。

6、若(x²+y²)(x²+y²-1)-12=0,则x²+y²=______________。

7、输电线的支架，起重机的支架都采用三角形结构，这是因为_____________。

8、两根木棒的长分别为8cm,10cm要选择第三根木棒，将它钉成一个三角形，那么第三根木棒的长x范围为____________。

9、在△ABC中，∠C=70°， ∠B-∠A=10°，则△ABC为 _________三角形（按角分类）。

10、一个零件形状如图（1），按规定∠A应是90°，∠B，∠C分别为21°和32°，检验工人量得∠BDC=148°，就判定这个零件不合格，为什么？______________________。

11、如图（2），△ABC中，∠C=90°，AD，BD分别平分 ∠CAB，∠ABC，则∠ADB=________。

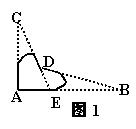
12、如图（3），AB=AC，若使△ABE≌△ACD，若以“SAS”为依据，还缺条件______________；若以“ASA”为依据，还缺条件_____________；若以“AAS”为依据，还缺条件_______________。

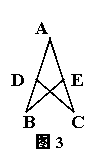
13、如图（4），BD平分∠ADE，∠A=90°，AB=AC，DE⊥BC，△DEC的周长为15cm，则BC= ________cm。

二、选择题（本题共8小题3分,第小题3分，共24分）

14、下列因式分解中错误的是　　　　　　　　　　　　　　　　  （　 ）A  1-9x² =(1+3x)(1-3x)　　　　　　  B  

C　–mx+my=- m(x+y)　　　　　　　  D ax-ay-bx+by=(x-y)(a-b)

15、下列各式中，能用平方差公式分解因式的是　　　　　　　　  （　 ）A  -a²-b² 　　 B　a²+(-b)²　　　 C　a²+(-b²)　　　D　(-a)²+b²

16、若x²+2(k-1)x+25是一个完全平方式，则k的值为　　　　　　 （　 ）

A　6　　　　 B　6或-4　　 　　C　±10　　　　 D　±5

17、把ab+a-b-1分解因式的结果为　　　　　　　　　　　　　　  （　 ）

A　（a+1）(b+1)　　　　　　　　　　 B　(a-1)(b-1)

C　（a+1）（b-1)　　　　　　　　　　 D　(a-1)(b+1)

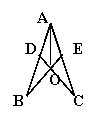18、在△ABC中，若∠A+∠B=2∠C,则∠C是　　　　　　　　　　　 （　 ）

A　30°　　　 B　90°　　 　　 C 45°　　　　  D 60°

19、如图（5），AB=AC，OB=OC，则

图中全等三角形的对数为　（　 ）

A  1　　　　  B　2

C　3　　　　  D　4

20、在△ABC和△A^‘B^’C^‘中，如果有（1）AB=A^’B^‘；（2）BC=B^‘C^’；（3）AC=

A^‘C^‘；（4）∠A=∠A^’；（5）∠B=∠B^‘；（6）∠C=∠C^’；不能保证△ABC≌

△A^‘B^’C^‘的是　　　　　　　　　　　　　　　　　　　　　　 　　(　　)

A　（1），（2），（3）　　　　　　　　　 B　（1），（2），（5）

C　（1），（3），（5）　　　　　　　　　 D　（2），（5），（6）

21、等腰三角形的一个角是40°,它的一腰上的高与底边的的夹角是　 （　 ）

A　20°　　　 B　50°　　　　 C 20°或50°　　 D 不能确定

三、把下列各式分解因式（本题共4小题，每小题3分，共12分）

22、(1)16（x+y）²-9(x-y)²　　　　　 (2)3a⁵b-12a³b+12ab

(3)ab(c²+d²)+cd(a²+b²)　　　　　　  (4)(b²+2b)²-7(b²+2b)-8

四、解答题（本题共6小题，共38分）

23、如图，在△ABC中按下列要求画图：（3分）

（1）画△ABC的中线CM；

（2）画△ABC的角平分线BE；

（3）画BC边上的高AD。

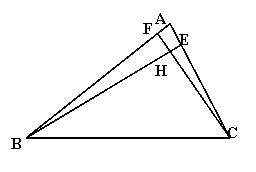24、已知：在△ABC中，∠ABC=66°，∠ACB=54°，BE⊥AC，垂足为点E，CF⊥AB，垂足为点F。求：∠ABE，∠BHC的度数。(6分)

25、已知：a、b、c为△ABC三条边的长，

（1）当b²+2ab=c²+2ac时，试判断△ABC属于哪一类三角形；

（2）求证：a²-b²+c²-2ac<0（10分）

26、求证：全等三角形对应角的角平分线相等（8分）

已知：

求证：

证明：

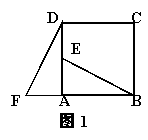
27、如图，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=AB。

（1）求证：△ABE≌△ADF；(3分)

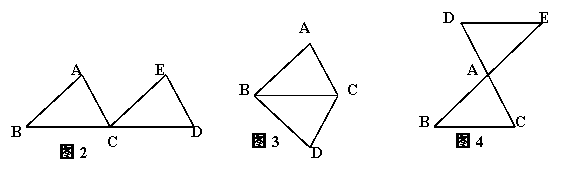
（2）阅读下面材料：如图2，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置；如图3，以BC为轴把△ABC翻折180°,可以变到△DBC的位置；如图4，以点A为中心，把△ABC旋转180°，可以变到△AED的位置。像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变大小的图形变换，叫做三角形的全等变换。

（3）回答下列问题：

（a）在图1 中，可以通过平行移动、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置。(2分)

（b）指出图1中线段BE和DF之间的关系并证明。(6分)