初二（下）数学期末评估卷
一、选择题（每题3分，共30分）
1、下列图形既是轴对称图形，又是中心对称图形的是（ ）
A、等边三角形 B、圆 C、平形四边形 D、等腰梯形
2、三角形的周长为20cm，它的三条中位线围成的三角形周长是（ ）
A、10cm B、12cm C、8cm D、16cm
3、正比例函数y= -3x的图象一定经过（ ）
A、第一、二象限 B、第一、三象限 C、第一、四象限 D、第二、四象限
4、若梯形中位线的长是高的2倍，面积是18cm2,则这个梯形的高为（ ）
A、6√2 cm B、6cm C、3√2 cm D、3cm
5、设双曲线y=k/x经过点（2，-1），则k的值为（ ）
A、-1 B、2
C、±2
D、-2
6、如图所示，⊙O的半径为2，弦AB=2√3，
那么弦心距长为（ ）
A、1/2 B、√3 C、1 D、√2
A B
7、已知一列数x,-2,4,-1,3的平均数为2，则x1为( )
A、-3 B、1 C、-4 D、6
8、一个圆锥的底面半径为6cm，高线长为8cm，则它的母线长为（ ）
A、8cm B、13cm C、10cm D、6cm
9、一杯水越来越凉，下列图象中表示这杯水的水温T（ºC）与时间t（分）的函数关系为（ ）
T（ºC）
T（ºC）
T（ºC）
T（ºC）
 |  | ||||
 | |||||
t（分）
t（分）
t（分）
t（分）
A
B
C
D
10、如图所示，AB为⊙O的直径，C、D、E都是⊙O上的点，则∠ACE+∠BDE=（ ）
A、90º
B、180º
C、80º
D、60º E
二、
填空题（每题3分，共30分）
11、横坐标为0的点都在 上。 A B
12、若正比例函数的图象经过点（1、4）请写出正比例函数的
解析式，如：
C
D
13、已知圆的半径为4cm,则45º圆心角所对的弧长是（ ）
14、如图已知AD是△ABC的高线，D，E，F分别是边BC，AB，AC的中点 A
连结DE，DF，EF，当△ABC满足
条件
时，使四边形AEDF为菱形。
E
F
（只填一个符合的条件）
B D C
15、若反比例函数y=k/x的图象在第一、三象限，则一次函数y=kx+1的图象在 象限
16、小灵通的通话收费标准为：前3分钟（不足3分钟按3分钟算）为0.2元，3分钟后每分钟收0.1元，则一次通话时间为x分钟，（x>3）与这次通话的费用y（元）之间的关系式为 。
17、小明坐车上学要经过两个红绿灯路口，车辆直接通过每一个红绿灯路口而不停车的概率为1/2，那么小明乘坐的车在两个路口都有不停车的概率是
。 C
18、如图，CD是⊙O的直径，AB是弦，CD⊥AB于点M，则可得出
AM=MB，AC=BC等多个结论，请你按现有图形再另外写两个成立的
结论
。 A
B
D
19、某函数具有两条性质：①图象关于原点成中心对称；②当x>0时，函数值y随自变量x的增大而减小，请举一例（用解析式表示）：
B
20、如图，扇形AOB的圆心角为直角，正方形OCDE内接于扇形， E
D F
点C，E，D分别在OA，OB，AB上，过点A作AF⊥ED交ED的延长线于F，
垂足为F，如果正方形长为1，那么阴影部分面积为 。
O C A
三、求解（证）题：（共40分）
21、（4分）已知平面直角坐标系上有6个点：A（2，2），B（1，1），C（8，1），D（6，4），
E（-1，-8），F（-3，-1/3）请将它们按下列要求分成两类，并写出同类点具有而另一类点不具有的一个特征。（将答案按要求写在横线上，特征不能用否定形式表述，点用字母表示）
甲类：点 、 是同一类点，其特征是
乙类：点 、 、 、 是同一类点，其特征是
22、（6分）如图，在□ABCD中，点E、F在对角线AC上，且AE=CF，请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）
（1）连结：
（2）猜想： =
（3）证明：
D C
A B
23、（9分）在争创卫生城市活动中，我区某校进行了一次“创卫”知识竞赛，竞赛成绩（得分取整数）进行整理后分成五组，并绘制成频率分布直方图，请结合如下图提供的信息，解答下列问题：
（1）该校共有多少名学生参赛？
（2）60.5---70.5这一分数段的频数、频率分别是多少？
（3）根据统计图，请你提出一个问题，并回答你提出的问题。
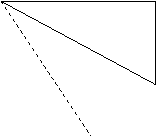
24、（6分）已知；把矩形AOBC放入直角坐标系XOY中，使OB、OA分别落在X轴、Y轴的正半轴上，点A的坐标为（0，2√3 ）连结AB，∠OAB=60º，将△ABC沿AB翻折，使C点落在该坐标平面内的D点处，AD交X轴于点E，求D点的坐标。
Y
A C
 |
X
O E B
D
25、（8分）阅读下面文字后，解答问题：
已知一次函数y=
图象过点A（0，3）B（1，-2）题目中的矩形框部分是一段被墨水污染无法辨认的文字。
（1）根据现有信息，你能否求出题中一次函数解析式？若能，请写出函数解析式；并画出图象、若不能、说明理由。
（2）小华说：“本题不用求函数解析式也能画出函数图象。”你认为他的说法正确吗？为什么？
26、（7分）如图，点A是半径为6/Лcm的⊙O上的一点，动点B、C同时从A点出发，分别以2cm/s,1cm/s的速度沿圆周作顺时针和逆时针方向运动。
（1）当运动1s时，求弦BC的长。
（2）请问第一次使弦BC成为⊙O的最长的弦时，动点B、C运动了多少时间？
A