临汾一中2005-2006学年度第一学期八年级期末试题（卷）
数 学
（试卷满分120分，答卷时间120分钟）
| 题号 | 一 | 二 | 三 | 四 | 总分 |
| 得分 |
|
|
|
|
|
一、填空题（每小题2分，共20分）
1．添括号：
（
） 。
2．计算：（1）
；（2）
。
3．函数
中自变量的x的取值范围是
。
4．直线
与x轴的交点坐标为
。
5．点P (1，2) 关于y轴对称的点P'的坐标是 。
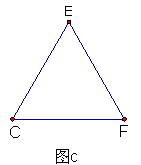
6．如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式 。
7．如图是2006年1月份的日历，观察图中有底色方框中的的9个数与方框正中心的数有什么关系。不改变方框的大小，将方框移动到另一个位置，若9个数之和为180，则此方框正中心的数字是 。
8．如图，在三角形纸片ABC中，∠C＝90°，∠A＝30°，AC＝3cm，折叠该纸片，使点A与点B重合，折痕与AC、AB分别相交于点D和点E，折痕DE的长为
cm。
9．若已知整式
是完全平方式，则
的值是 。
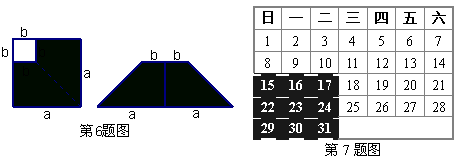
10．如图，沿着大正三角形的对称轴对折，则互相重合的两个小正三角形内的单项式的乘积为
。
二、选择题（每小题3分，共30分）
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 |
11．下列图案是我国几家银行的标志，其中是轴对称图形的有（ ）
A．4个 B．3个 C．2个 D．1个
12．下列运算正确的是（ ）
A．
B．
C．
D．
13．计算：
值为（ ）
A．2
B．
C．
D．
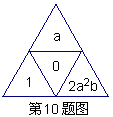
14．如图，在△ABC中，BC=8cm，AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长等于18cm ，则AC的长为（）
A．6cm B．8cm C．10cm D．12cm
15．如图，OP平分∠AOB，PC⊥OA于C，PD⊥OB于D，则PC与PD的大小关系（ ）
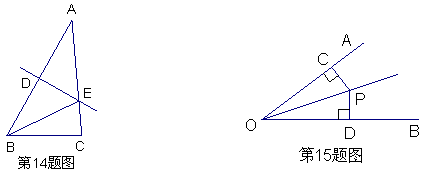A．PC＞PD B．PC＝PD C．PC＜PD D．不能确定
16．在直角坐标系中，O为坐标原点，已知A（2，2），在x轴的正半轴上确定点P， 使△AOP为等腰三角形，则符合条件的点P的个数共有（ ）
A．1个 B．2个 C．3个 D．4个
17． 为了解某校男生的身高情况，随机抽取了若干名男生进行身高测量，将所得数据整理后，画出频数分布直方图。如图，则抽取的男生人数为（ ）
A. 44名 B. 46名 C. 48名 D. 50名
|
|
|
|
|
|
|
18． 小颖在做下面的数学作业时，因钢笔漏墨水，不小心将部分字迹污损了。作业过程如下：
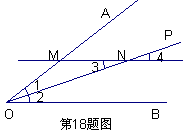已知：如图，OP平分∠AOB，MN∥OB。求证：OM=NM。
证明：∵OP平分∠AOB
∴
又∵MN∥OB
∴
∴∠1=∠3
∴ OM=NM。
小颖思考：污损部分字迹应分别是以下四项中的二项：①∠1=∠2 ②∠2=∠3 ③∠3=∠4
④∠4=∠1。 那么她补充出来的结果应是（ ）
A．①② B．②③ C．①④ D．③④
19． 将一正方形纸片按图中⑴、⑵的方式依次对折后，再沿⑶中的虚线裁剪，最后将⑷中的纸片打开铺平，则所得图案应该是下面图案中的( )
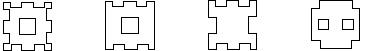
A B C D
20．如图，已知在等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是（ ）
A. 40O B. 55O
C. 60O D. 75O
三、解答题
21．（本题12分）
（1）分解因式：①
②
（2）先化简，再求值：
，其中
22．（本题8分）
下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习等腰三角形有关内容后, 张老师请同学们交流讨论这样一个问题: “已知等腰三角形ABC的∠A等于30°, 请你求出其余两角。”
同学们经片刻的思考与交流后, 李明同学举手说: “其余两角是30°和120°”； 王华同学说: “其余两角是75°和75°。” 还有一些同学也提出了不同的看法……
（1）假如你也在课堂中, 你的意见如何? 为什么?
（2）通过上面数学问题的讨论, 你有什么感受? (用一句话表示)
23．（本题8分）如图，有一条小船，
（1）若把小船平移，使点A平移到点B，请你在图中画出平移后的小船；（5分）
（2）若该小船先从点A航行到达岸边L的点P处补给后，再航行到点B，但要求航程最短，试在图中画出点P的位置（3分）
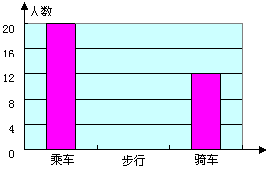24．（本题8分）如图是某班学生外出乘车、步行、骑车的人数分布条形图和扇形分布图。
（1）求该班有多少名学生？
（2）补上“步行”分布条形图的空缺部分。
（3）在扇形统计图中，求骑车人数所占的圆心角度数。
（4）若全年级有500人，估计该年级步行人数。
25．(本题6分) 以下每幅均是由边长为1cm的小正方形构成的4×4网格。
（1）请观察图①-④中的阴影部分构成的图案，写出这四个图案都具有的两个共同特征；
特征之一： ；
特征之二： 。
（2）借助图之⑤的网格，请设计一个新的图案，使该图案同时具有你在解答（1）中所写出的两共同特征。（注：新图案与①-④图案不能重合。）
26．(本题8分)如图，已知：在△ABC中，AB=AC，∠A＝36°，∠DBC＝36°。
（1）分别计算∠1，∠2的度数。
（2）直接说明图中有哪些等腰三角形。
27．(本题8分)在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数S（次/分）是这个人年龄n（岁）的一次函数。
 | |||
 | |||
（1）根据以上信息，求在正常情况下，S关于n的函数关系式；
（2）若一位63岁的人在跑步，医生在途中给他测得10秒心跳为2 6次，问：他是否有危险？为什么？
四、探索题
28．(本题12分) 如图a，△ABC和△CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF和BE。
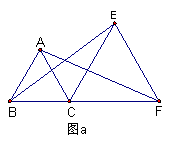(1)线段AF和BE有怎样的大小关系? 请证明你的结论；
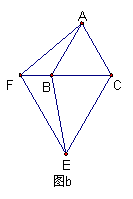
(2)将图a中的△CEF绕点C按逆时针旋转180O，得到图b，(1)中的结论还成立吗?作出判断并说明理由；
