第一章勾股定理
主干知识梳理
1． 直角三角形边、角之间的关系
2． 勾股定理的逆定理
例1如图，一只螳螂在树干的A点处，发现它的正上方B点处有一只小虫子，螳螂想扑到这只小虫子，但又怕被发现，于是饶到虫子的背后吃掉它，已知树干的半径为10厘米，AB两点间的距离为45厘米，(π的值取3)，求螳螂绕行的距离。
例2如图，一只蚂蚁沿长方体的表面从A点爬到Bˊ点，那么沿哪条路最近？最短路程为多少？已知长方体的长为2厘米，宽为1厘米，高为4厘米。
例3在一棵树的10米高处有两只猴子，其中一只猴子爬下树走到离树20米处的池塘A处，另一只爬到树顶后直接跃向池塘A处，如果两只猴子经过的距离相等，求这棵树的高度。
例4某村在两个山丘之间修建了一个三角形的水库，经了解，水库的平均水深是10米，三条岸边的长度分别为63米，30米，51米，求水库的蓄水量大约是多少？
例5李伟从家里出发，若向正东走900米，再折向正北走300米，就到了小红家；若先向正北走900米，再折向正东走100米，就到了小兰家。求小红家和小兰家相距多远？
练习
一、 填空题:
1. 一个三角形的三个内角之比为1：2：3，则此三角形是__________三角形；若此三角形的三边为a,b,c，则此三角形的三边的关系是__________。
2. 在△ABC中，若AB2
+BC2 = AC2,则∠A+∠C=___________度。
3. 一个直角三角形的三边长为三个连续自然数，
则它的三边长为____________。
4．一座桥横跨一江，桥长12m，一般小船自桥北头出发，
向正南方驶去，因水流原因到达南岸以后，发现已
偏离桥南头5m，则小船实际行驶_______m。
5．在Rt△ABC中，∠C=900,AB=13,AC=5,则BC=__________.
6. 一个三角形的三边的比为5：12：13，它的周
长为60cm,则它的面积是__________。
7. 如图（1），在Rt△ABC中，∠C=900,BC=15,AC=17,
以AB为直径作半圆，则此半圆的的面积为_______。
8. 如图（2）是一个长方体，阴影部分的面积为__________。
9．△ABC的三边为a、b、c，且满足条件：a2c2－b2c2=a4－b4，试判断三角形的形状.
解：∵a2c2－b2c2=a4－b4……① c2(a2－b2)=(a2+b2)(a2－b2)……②
∴c2=a2+b2……③ ∴△ABC为直角三角形……④
上述解答过程中代码_________出现错误；正确答案应为△ABC是_________三角形.
10三角形的两直角边是3,4,则以斜边长为直径的圆的面积是_______________.
11已知正方形的面积为16cm
,以这个正方形的边长为边作等边三角形,则其一边上的高的平方等于_____________.
二、选择题
12.有五组数：①25，7，24；②16，20，12；③9，40，41；④4，6，8；⑤32,42,52，以各组数为边长，能组成直角三角形的个数为( ).
A.1 B.2 C.3 D.4
13.下列结论错误的是（ ）.
A．三个角度之比为1∶2∶3的三角形是直角三角形
B．三个边长之比为3∶4∶5的三角形是直角三角形
C．三个边长之比为8∶16∶17的三角形是直角三角形
D．三个角度之比为1∶1∶2的三角形是直角三角形
14.如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是( ).
A.7,24,25
B.3
,4,5
C.3,4,5 D.4,7,8
15.如果把直角三角形的两条直角边同时扩大到原来的2倍，那么斜边扩大到原来的( )
A.1倍 B. 2倍 C. 3倍 D. 4倍
16.一块木板如图所示，已知AB=4，BC=3，DC=12，AD=13，∠B=900，木板的面积为( ).
A.60 B.30 C.24 D.12
17．三角形的三边长分别为6,8,10，它的最短边上的高为( ).
A.6 B.4.5 C.2.4 D.8
18．直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )
A. ab=h
B. a
+b=2h; C. 
+
=
D. 
+
=
19. 下列各组线段中的三个长度①9、12、15；②7、24、25；③32、42、52；④3a、4a、5a（a>0）；⑤m2-n2、2mn、m2+n2（m、n为正整数，且m>n）其中可以构成直角三角形的有（ ）
A、5组； B、4组； C、3组； D、2组
三、解答题
20如图，一架2.5米长的梯子AB，斜靠在一竖直的墙AC上，这时梯足B到墙底端C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯足将向外移多少米？
21如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多少米?
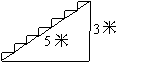
22已知:
ABC中,CD
AB于D, AC=4, BC=3, BD=
.
(1) 求CD的长;
(2) 求AD的长;
(3) 求AB的长;
(4)判断 ABC的形状。
23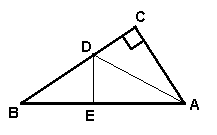
如图，有一个直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上,且与AE重合,你能求出CD的长吗？