2006年芜湖市鸠江区初中数学竞赛试题
| 题号 | 一 | 二 | 三 | 总分 | |||
| 第1~5题 | 第6~10题 | 第11题 | 第12题 | 第13题 | 第14题 | ||
| 得分 | |||||||
一、选择题(本题有5小题,每小题6分,共30分)
每小题都只有一个答案是正确的,多选不给分
1.如果多项式![]() ,则
,则![]() 的最小值是
( )
的最小值是
( )
(A)2005 (B)2006 (C)2007 (D)2008
2.一架天平因为两臂的长不相等,所以称得物体质量不准.要是把某物体放在天
平的左盘,称得质量是![]() 克,把这一物体放在天平的右盘,称得质量是
克,把这一物体放在天平的右盘,称得质量是![]() 克,那么这个物体的准确质量(单位:克)是
( )
克,那么这个物体的准确质量(单位:克)是
( )
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
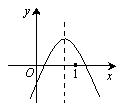
3.函数![]() 图象的大致位置如右图所示,则
图象的大致位置如右图所示,则
![]() 等代数式
等代数式
的值中,正数有 ( )
(A)2个 (B)3个 (C)4个 (D)5个 (第3题图)
4.某工厂实行计时工资制,每个工人工作1小时的报酬是6元,一天工作8小时.但是用于计时的那口钟不准:每69分钟才使分针与时针重合一次,因此工厂每天少付给每个工人的工资是 ( )
(A)2.20元 (B)2.40元 (C)2.60元 (D)2.80元
5.2条相交的弦把圆分成4部分,3条两两相交的弦最多能把圆分成7部分,如果两两相交的k条弦最多能把圆分成n部分,那么两两相交的k+1条弦最多能把圆分成几部分?答:( )
(A)n+1 (B)2n (C)n+k (D)n+k+1
 二、填空题(本题有5小题,每小题6分,共30分)
二、填空题(本题有5小题,每小题6分,共30分)
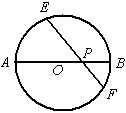
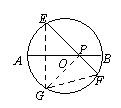
6.如图,⊙O的直径AB与弦EF相交于点P,交角为45°,
若![]() =8,则AB等于 .
=8,则AB等于 .
7.若![]() ,
,![]() ,则
,则![]() .
.
8.已知不论![]() 取何数值,分式
取何数值,分式![]() 的值都为同一个定值,
(第6题图)
的值都为同一个定值,
(第6题图)
那么![]() 的值为
.
的值为
.
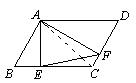
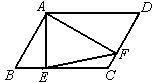 9.如图,在□ABCD中,∠B=60°,AE⊥BC,AF⊥CD,E,F为垂足. 设□ABCD的面积为 S,则△AEF的面积为 .
9.如图,在□ABCD中,∠B=60°,AE⊥BC,AF⊥CD,E,F为垂足. 设□ABCD的面积为 S,则△AEF的面积为 .
10.若二次函数![]() 的图象的顶点在
的图象的顶点在
第一象限,且过点(0,1)和(-1,0).
则![]() 的值的变化范围是
.
的值的变化范围是
.
(第9题图)
三、解答题(本题有4小题,每小题15分,共60分)
11.甲、乙两辆公共汽车分别自A、B两地同时出发,相向而行.甲车行驶85千米后与乙车相遇,然后继续前进.各车到达对方的出发点等候30分钟立即依原路返回.当甲车行驶65千米后又与乙车相遇,求A、B两地距离.
12.如图,四边形ABCD内接于以BC为直径的半圆O,且AB=AD,DA、CB的延长线相交于点P,CE⊥PE,PB=BO.已知DC=18,求DE的长.
13.(1)试设计一种方法,把一个正方形不重复不遗漏地分割成8个正方形(分得的正方形大小可以不相同);又问如何把正方形按上述要求分成31个正方形?
(2)试设计一种方法,把一个立方体分割成55个立方体(要求:不重复不遗漏,分得的立方体大小可以不相同).
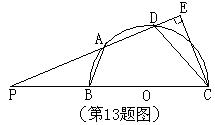
 14.如图,AB、CD是半径为1的⊙P两条直径,且∠CPB=120°,⊙M与PC、PB及弧
14.如图,AB、CD是半径为1的⊙P两条直径,且∠CPB=120°,⊙M与PC、PB及弧![]() 都相切,O、Q分别为PB、弧
都相切,O、Q分别为PB、弧![]() 上的切点.
上的切点.
(1)试求⊙M的半径![]() ;
;
(2)以AB为![]() 轴,OM为
轴,OM为![]() 轴(分别以OB、OM为正方向)建立直角坐标系,
轴(分别以OB、OM为正方向)建立直角坐标系,
①设直线![]() 过点M、Q,求
过点M、Q,求![]() ,
,![]() ;
;
 ②设函数
②设函数![]() 的图像经过点Q、O,求此函数解析式;
的图像经过点Q、O,求此函数解析式;
③当![]() <0时,求x的取值范围;
<0时,求x的取值范围;
④若直线![]() 与抛物线
与抛物线![]() 的另一个交点为E,求线段EQ
的另一个交点为E,求线段EQ
的长度.
2006年鸠江区初中数学竞赛参考答案
一、选择题(每小题5分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | B | B | A | C | D |
1.B
![]() ,故最小值为2006.
,故最小值为2006.
2.B
设物体的准确质量为x,左右两臂长分别为a,b,则![]() .
.
两式相乘,约去正数ab,得![]() .
.
3. A
显然,![]() 由
由![]() ,得
,得![]() ,所以
,所以![]() ;
;
由a-b+c<0得![]() ;
;
由a+b+c>0得a+b>-c>0,因此![]() .
.
综上所述,仅有![]() 为正数.
为正数.
4.C
正常的时钟,分针与时针重合一次的时间为![]() 分,因此,工人一天实
分,因此,工人一天实
际工作时间为 (小时),超过
(小时),超过![]() (小时).
(小时).
少付工资![]() 元.
元.
5.D
第k+1条直线与前面的k条直线都相交,且不经过原有的任何一个交点,因此
把前k条直线为边界的(k+1)个区域一分为二,增加了(k+1)个区域,结
果区域总数成为n+k+1.
 二、填空题(每小题6分,共30分)
二、填空题(每小题6分,共30分)
6.4
作E关于AB的对称点G,则PG=PE,PG⊥PE,
![]() .
.
但FG所对的圆周角为45°,所以FG所对的圆心角为90°,圆的半径为2.
7.![]()
![]() ,
,
∴![]() .
.
8.![]()
当![]() 时,分式值为
时,分式值为![]() .
.
所以当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
 9.
9.![]()
由△ABE∽△ADF得![]() ,即
,即![]() ,
,
易证∠B=∠EAF,可知△AEF∽△ABC,相似比为![]() .
.
但△ABC的面积为![]() ,所以△AEF的面积为
,所以△AEF的面积为![]() .
.
10.![]()
分别令![]() ,
,![]() 和
和![]() ,
,![]() ,求得
,求得![]() ,
,![]() ,∴
,∴![]() .
.
由题设知,![]() ,∴
,∴![]() .又由
.又由![]() 及
及![]() 可知
可知![]() .
.
∴![]() .
.
三、解答题(每小题15分,共60分)
11.设甲车的速度为x(千米/时),乙车的速度为y(千米/时),A、B两地的距离为S(千米) …………(2分)
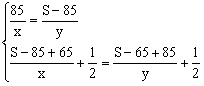 则
则
…………(6分)
 即
…………(8分)
即
…………(8分)
①÷②得 ![]() …………(12分)
…………(12分)
去分母,化简得S2-190S=0
S=0(舍) S=190 …………(14分)
答:A、B两地的距离为190千米。 …………(15分)
 12.如图,连结
12.如图,连结![]() ,
,![]() .……(1分)
.……(1分)
由![]() 知,
知,![]() .…(2分)
.…(2分)
又![]() ,
,
所以![]() ,
,![]() ∥
∥![]() .…(4分)
.…(4分)
∵ ![]() ,
,
∴ ![]() ,
,![]() .…(6分)
.…(6分)
由切割线定理知
![]() ·
·![]() ·
·![]() ,
,![]() ·
·![]() ,……(8分)
,……(8分)
∴ ![]() . ∴
. ∴ ![]() .…………(10分)
.…………(10分)
∵ ![]() △
△![]() ∽
∽![]() △
△![]() ,…(12分)
,…(12分)
∴ ![]() ,
,![]() ,…(14分)
,…(14分)
∴ ![]() .…………(15分)
.…………(15分)
13.(1)容易把一个正方形分成42=16个正方形,再把其中位于一角的9个拼成一个正方形,共得:16﹣9+1=8个正方形. …………(5分)
分成16个正方形后,把其中任意5个分成4个小正方形,共有16﹣5+5×4=31个正方形. …………(10分)
(2)把立方体分割成33=27个立方体,再把其中4个各分成23=8个立方体,共27﹣4+4×23=55个立方体. …………(15分)
14.(1)由![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,
得 ![]()
![]()
![]() -
-![]() .
…………(2分)
.
…………(2分)
(2)①点![]() ,即
,即![]() ;点
;点![]() ,即
,即![]() .
.
![]() 由已知直线过点
由已知直线过点![]() 、
、![]() ,得
,得 ![]() ,
,
![]() ,
,
解得 ![]() ,
,![]() . …………(5分)
. …………(5分)
②由![]() 过点
过点![]() 、
、![]() ,则
,则
![]() ,
,
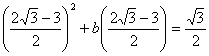 ,得
,得 ![]() ,
,
即得 ![]() .
…………(8分)
.
…………(8分)
③令![]() ,则
,则![]() ,
,![]() ,
,
即得 当![]() 时,
时,![]() .
.
![]() ④由已知得
④由已知得 ![]() ,
,
![]() ,
,
消去![]() ,得
,得 ![]() . …………(12分)
. …………(12分)
设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,
,
由根与系数的关系得 ![]() ,
,
则![]() …………(14分)
…………(14分)
进而得线段![]() 的长为
的长为![]() .
…………(15分
.
…………(15分