徐州矿务集团一中期末测试数学试题
一、选择题（本大题共10小题，每小题3分，共30分．下列各题的四个选项中，只有一个选项是符合题意的）
1．如果□+2=0，那么“□”内应填的实数是
A．－2
B．－
C．
D． 2
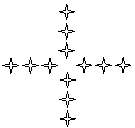2．下列基本图形中，经过平移、旋转或轴对称变换后，不能得到右图的是
A． B．
 | |||
 | |||
C. Ｄ．
3．下列统计量中，能反映一名同学在7～9年级学段的学习成绩稳定程度的是
A．平均数 B．中位数 C．众数 D．方差
4．下列关于
的说法中，错误的是
A．是无理数
B．3＜＜4
C．是12的算术平方根 D．不能再化简
5． 右图需再添上一个面，折叠后才能围成一个正方体，下面是四位同学
补画的情况（图中阴影部分），其中正确的是
A． Ｂ． Ｃ． Ｄ．
6．右图是创星中学的平面示意图，其中宿舍楼暂未标注，已知宿舍楼在教学楼的北偏东约300的方向，与教学楼实际距离约为200米，试借助刻度尺和量角器，测量图中四点位置，能比较准确地表示该宿舍楼位置的是
A． 点A Ｂ．点B
Ｃ．点C D．点D
7．如图，小亮同学在晚上由路灯A走向路灯B，当他走到点P时，发现他的身影顶部正好接触路灯B的底部，这时他离路灯A 25米，离路灯B 5米，如果小亮的身高为1.6米，那么路灯高度为
A．6.4米
B． 8米
C．9.6米
D． 11.2米
8．四张完全相同的卡片上，分别画有圆、矩形、等边三角形、等腰梯形，现从中随机抽取一张，卡片上画的恰好是中心对称图形的概率为
| |
B． C．
D．1
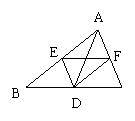9．如图，点D、E、F分别是△ABC（AB＞AC）各边的中点，下列说法中，错误的是
A． AD平分∠BAC
|
BC
C． EF与AD互相平分
D． △DFE是△ABC的位似图形
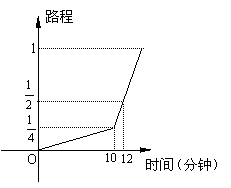10．一名考生步行前往考场，
10分钟走了总路程的，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1），则他到达考场所花的时间比一直步行提前了
A． 20分钟
Ｂ．22分钟
Ｃ．24分钟
D．26分钟
二、填空题（本大题共6小题，每小题3分，共18分．把正确答案直接填在题中的横线上）
 |
11．如果a+b=2005，a－b=1，那么a2－b2= ．
12．如图，已知AB∥CD，CE、AE分别平分∠ACD、∠CAB，
则∠1+∠2= ．
13．下列命题：①对顶角相等；②等腰三角形的两个底角相等；③两直线平行，同位角相等．其中逆命题为真命题的有： （请填上所有符合题意的序号）．
14．把棱长为1cm的四个正方体拼接成一个长方体，则在所得长方体中，表面积最大的值等于 cm2．
15．函数y=
的图象如图所示，在同一直角坐标系内，如果将直线y=－x+1沿y轴向上平移2个单位后，那么所得直线与函数y=的图象的交点共有
个。
16．已知一列数：1，―2，3，―4，5，―6，7，… 将这列数排成下列形式：
第1行 1
第2行 －2 3
第3行 －4 5 －6
第4行 7 －8 9 －10
第5行 11 －12 13 －14 15
… …
按照上述规律排下去，那么第10行从左边数第5个数等于 ．
三．解答题 (本大题共11小题,共102分)
17． (本题满分8分)计算：
·
－(2－π)0－()－1．
18．(本题满分8分)化简：（1+
）÷
．
19．(本题满分8分)
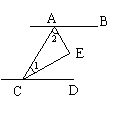
如图是不倒翁的正视图，不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B，不倒翁的鼻尖正好是圆心O，若∠OAB=25°，求∠A PB的度数．
20．(本题满分8分)已知不等式：⑴1－x＜0；⑵
＜1；⑶ 2x+3＞1；⑷ 0.2x－3＜－2．你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来．
21．(本题满分8分)对于二次三项式x2－10x+36，小聪同学作出如下结论：无论x取什么实数，它的值都不可能等于11．你是否同意他的说法？说明你的理由．
22．(本题满分10分)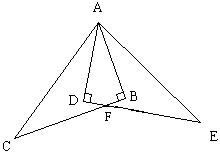 
已知：如图，Rt△ABC≌Rt△ADE，∠ABC＝∠ADE=900，试以图中标有字母的点为端点，连结两条线段，如果你所连结的两条线段满足相等、垂直或平行关系中的一种，那么请你把它写出来并证明．
23．(本题满分10分)为了调查淮安市今年有多少名考生参加中考，小华从全市所有家庭中随机抽查了200个家庭，发现其中10个家庭有子女参加中考．
⑴本次抽查的200个家庭中，有子女参加中考的家庭的频率是多少？
⑵如果你随机调查一个家庭，估计该家庭有子女参加中考的概率是多少？
⑶已知淮安市约有1.3×106个家庭，假设有子女参加中考的每个家庭中只有一名考生，请你估计今年全市有多少名考生参加中考?
24．(本题满分10分)
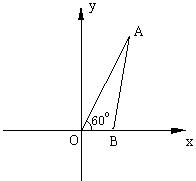如图,在平面直角坐标系中,∠AOB=60°,点B坐标为（2，0），线段OA的长为6． 将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处．
⑴请在图中画出△COD;
⑵求点A旋转过程中所经过的路程（精确到0.1）；
⑶求直线BC的解析式．
25．(本题满分10分) 
已知： ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．
⑴求证：四边形ABCD是矩形；
⑵在四边形ABCD中，求
的值．
26．(本题满分10分)快乐公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如右表所示．
|
| 甲 | 乙 | 丙 |
| 优品率 | 80% | 85% | 90% |
⑴求快乐公司从丙厂应购买多少件产品Ａ；
⑵求快乐公司所购买的200件产品A的优品率；
⑶你认为快乐公司能否通过调整从三个工厂所购买的产品A的比例，使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．
| 得分 | 阅卷人 | 复卷人 |
27．(本题满分12分)
课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：
⑴方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米2，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．
⑵假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．
恭贺你顺利完成答题，别忘了认真检查！