2005—2006学年第二学期九年级数学测试(一)
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 总分 |
| 得 分 | |||||||||
| 复核人 |
一、选择题(每小题2分,共24分)
1.若![]() 与
与![]() 互为相反数,则
互为相反数,则![]() 的值为-------------------------------------( )
的值为-------------------------------------( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.比![]() 小
小![]() 的数是-----------------------------------------------------( )
的数是-----------------------------------------------------( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3.计算![]() 的结果是-------------------------------------------------( )
的结果是-------------------------------------------------( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. ![]() 的算术平方根是--------------------------------------------------( )
的算术平方根是--------------------------------------------------( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.反比例函数![]() 的图象经过点
的图象经过点![]() ,则
,则![]() 的值为---------------------( )
的值为---------------------( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6.某种禽流感病毒变异后的直径为![]() 米,将这个数写成科学记数法是( )
米,将这个数写成科学记数法是( )
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C.![]() 米 D.
米 D. ![]() 米
米
7. 二次函数![]() 的图象的对称轴是-----------------------------( )
的图象的对称轴是-----------------------------( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则该目标的坐标可能是-----------------------------------------------------------( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
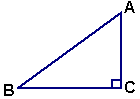
9.已知如图,在△ABC中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为----( )
的值为----( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 如图,点D在以AC为直径的⊙O上,如果∠BDC=20°,那么∠ACB的度数为-( )
A. 20° B. 40° C. 60° D. 70°
11.面积为10的正方形的边长![]() 满足下面不等式中的-----------------------( )
满足下面不等式中的-----------------------( )
 A.1<
A.1<![]() <3 B. 3<
<3 B. 3<![]() <4 C. 5<
<4 C. 5<![]() <10 D. 10<
<10 D. 10<![]() <100
<100

第8题 第9题 第10题
12.某圆锥的主视图是一个边长为![]() 的等边三角形,那么这个圆锥的侧面积是( )
的等边三角形,那么这个圆锥的侧面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(每小题2分,共12分)www.1230.org 初中数学资源网
13.分解因式:![]() ____
___.
____
___.
14.请写出一个满足下列条件的函数:当![]() >0时,函数值
>0时,函数值![]() 随着
随着![]() 增大而增大
增大而增大
.
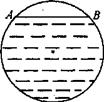
15.某居民小区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图所示,污水
水面宽度为60cm,水面至管道顶部距离为10cm,修理人员应准备 cm内径的管道.
16.在比例尺为1∶40000的地图上,某经济开发区的面积为![]() ,那么,该经济开发区
,那么,该经济开发区
的实际面积为
![]() .
.
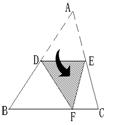
17.如图,D、E为△ABC两边AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=55°,则∠BDF= °.
18.如图,四边形ABCD是一个矩形,E、F、G、H分别是边AD、BC上的三等分点,
请你根据图中的数据求阴影部分的面积为 cm2.
 | ||||||||||
|
|
| ||||||||

三、(19-21小题每小题5分,22题6分,共21分)
19. ![]() 20. 解方程组:
20. 解方程组:![]()
21. 求不等式组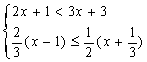 的非负整数解.www.1230.org
初中数学资源网
的非负整数解.www.1230.org
初中数学资源网
22.已知如图,在□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:CD=FA.
(2)若使∠F=∠BCF,□ABCD的边长之间还需再添加什么条件?请你补上这个条件,并进行证明(不要再添加辅助线)

四、(每小题6分,共12分)
23. 一布袋中放有红、黄、白三种颜色的球各一个,它们除颜色外其他都一样,小亮从布袋中摸出一个球后放回去摇匀,再摸出一个球.
(1)小亮第一次恰好摸出一个白球的概率是多少?
(2)请你利用列举法(列表或画树状图)分析并求出小亮两次都能摸到白球的概率.
24.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,请你计算出学校旗杆的高度.

五、(25题8分,26题6分,共14分)
25.某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
| 年 度 | 2002 | 2003 | 2004 | 2005 |
| 投入技改资金z(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本,(万元/件) | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,找出一个适合上表的y与x之间的关系式,
(2)按照这种变化规律,若2006年已投人技改资金5万元.
①预计生产成本每件比2005年降低多少万元?
②如果打算在2006年把每件产品成本降低到3.2万元,则还需投入技改资金多少万元(结果精确到0.01万元)?
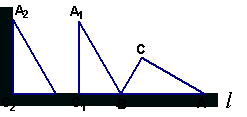
26. 如图,在一个横截面为Rt△ABC的物体中,∠ACB=∠CAB=30°,BC=2米.工人
师傅把此物体搬到墙边,先将AB边放在地面(直线![]() )上,再按逆时针方向绕点B翻转到△
)上,再按逆时针方向绕点B翻转到△![]() 的位置(
的位置(![]() 在
在![]() 上),最后沿
上),最后沿![]() 的方向平移到△
的方向平移到△![]() 的位置,其平移的距离为线段AC的长度(此时
的位置,其平移的距离为线段AC的长度(此时![]() 恰好靠在墙边).
恰好靠在墙边).
(1)请直接写出AB、AC的长;
(2)画出在搬动此物的整个过程A点所经过的路径,求出该路径的长度.
(结果精确到0.1米,![]() ,
,![]() ,
,![]() )
)
 |
六、(27题8分,28题6分,共14分)
27. 小明就本班同学参加各项体育运动的情况进行了一次调查,图1和图2是他根据调查所得的数据绘制的两份不完整的统计图,请你根据图中提供的有关信息回答以下问题:
(1)求该班有多少名学生?
(2)在图1中将表示“田径”的部分补充完整;
(3)在扇形统计图中,计算出表示“其它”部分所对应的圆心角的度数;
(4)若全年级有500人,请你估算出全年级参加“田径运动”的人数.
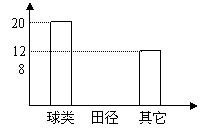
 |
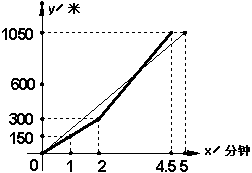
28.端午节期间,南京市都将举行龙舟比赛。甲、乙两支龙舟队在比赛时的路程y(米)与时间x(分钟)之间的函数图象如图所示(其中实线表示乙队,虚线表示甲队).请你根据图象回答下列问题:
(1)1.8分钟时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?先到达多少时间?
(3)求乙队加速后,路程y(米)与时间x(分钟)之间的函数关系式。
| |
七(29题8分,30题5分,共13分)
29.数学兴趣小组几名同学到某商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱70元销售平均每天销售30箱,价格每降低1元平均每天可多销售3箱.老师要求根据以上资料,解答下列问题,你能做到吗?
⑴ 写出平均每天销售量y(箱)与每箱售价x(元)之间的函数关系;
⑵ 写出平均每天销售利润W(元)与每箱售价x(元)之间的函数关系;
⑶ 现该商场要保证每天盈利900元,同时又要使顾客得到实惠,那么每箱售价为多少元?
⑷ 你认为每天赢利900元,是牛奶销售中的最大利润吗?为什么?
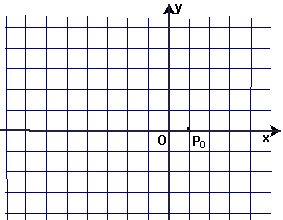
30. 在平面直角坐标系中有一点P0(1,0),O为坐标原点.将线段OPO绕点O按逆时针旋转45º得线段OP1,延长OP1到点P2,使OP2= 2OP1.再将OP2绕点O按逆时针方向旋转45º得线段OP3 ,延长OP3到点P4,使OP4= 2OP3.照此规律,继续下去.试写出P2、P7、P100三个点的坐标.
 |
八(10分)
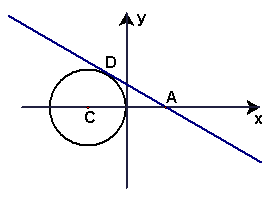
31.已知如图,在直角坐标系中,⊙C与![]() 轴相切,且C点的坐标为
轴相切,且C点的坐标为![]() ,直线
,直线![]() 过点
过点![]() 且与⊙C切于点D,
且与⊙C切于点D,
(1)∠DAC= º;
(2)求直线![]() 的解析式;
的解析式;
(3)若在直线![]() 上存在一点P,使△APC为等腰三角形,求P点的坐标.
上存在一点P,使△APC为等腰三角形,求P点的坐标.
2005—2006学年第二学期九年级数学测试(一)
答 案
一、选择题(每小题2分,共24分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 | C | C | D | B | A | C |
| 题号 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | A | D | B | A |
二、填空题(每小题2分,共12分)
13.x(x+2)(x-2)
14.答案不唯一,如:y=x
15. 100 16. 3.2
17. 70 18. 200
三、(19-21小题每小题5分,22题6分,共21分)
19.原式=![]() ……2分
……2分
![]() ……4分
……4分
![]() ……5分
……5分
20.原方程可化为:x=2(x-3) …2分
解得:x=6 ……3分
经检验:x=6是原方程的根 ……5分
21.由①得:x>-2 ……1分
由②得:x≤5 ……3分
∴由①、②得 -2<x≤5 ……4分
它的非负整数解为:
x =0、1、2、3、4、5 ……5分
22.⑴在□ABCD中:
∵∠D=∠EAF,∠DEC=∠AEF
DE=AE
∴△DEC≌△AEF ……2分
∴CD=FA ……3分
⑵补条件:BC=2DC(或AD=2DC=2AB)……1分
证明:∵BC=2DC,DC=2AB,DC=FA
∴BC=DC+AF=AB+AF=BF ……2分
∴△CBF为等腰三角形 ……3分
∴∠F=∠BCF
四、(每小题6分,共12分)
23.⑴P(摸出白球)=![]() ……2分
……2分
⑵列表或画树状图正确 ……2分
P(二次摸出白球)=![]() ……4分
……4分
24.解:设旗杆的高度为x米,延长AC交BD的延长线于点E.
由题意得;![]() ,
,
![]() ……2分
……2分
又∵△CDE∽△ABE
∴ ![]() ……4分
……4分
∴![]() (米)…5分
(米)…5分
答:旗杆的高度为10米. …6分
五、(25题8分,26题6分,共14分)
25.⑴由表中数据的对应关系可知xy=18,
∴y是x的反比例函数,且![]() …3分
…3分
⑵①当x=5时,代入得y=3.6(万元/件)
4-3.6=0.4(万元/件)
∴比05年每件成本降低0.4万元 …1分
②当y=3.2时,x≈5.63(万元)
5.63-5=0.63(万元)
∴还需投入技改资金约0.63(万元)
26. ⑴![]() , ………1分
, ………1分
![]() 米
………2分
米
………2分
⑵正确画出A点路线 ………3分
路线长:
![]() ……5分
……5分
![]() ………6分
………6分
六、(27题8分,28题6分,共14分)
27. ⑴由图得![]() …2分
…2分
⑵![]()
在图(1)中正确补上图形 …4分
⑶由图知“其它”占30%,所对的圆心角的度数为![]() …6分
…6分
⑷参加“田径”的人数为:
![]() …6分
…6分
28. ⑴甲队处于领先位置 ……1分
⑵乙队先到终点 ……2分
先到0.5分钟 ……3分
⑶设![]()
由题意得![]()
解得![]() ……5分
……5分
∴乙队加速后,关系式为
![]() ……6分
……6分
七(29题8分,30题5分,共13分)
29. ⑴![]()
![]() ……2分
……2分
⑵![]()
![]() ……4分
……4分
⑶当![]() 时,
时,
![]() ……5分
……5分
![]()
∴![]() ……5分
……5分
∵要使顾客得到实惠,∴![]() 舍去
舍去
∴每箱价格定为50元 ……6分
⑷由![]() 得
得
![]()
![]() (元) ……7分
(元) ……7分
∴赢利900元不是销售的最大利润 8分
30.![]() ……1分
……1分
![]() …3分
…3分 ![]() ……5分
……5分
八(10分)
31. ⑴![]() ……1分
……1分
⑵得出![]() 与
与![]() 轴的交点
轴的交点![]()
![]() …2分
…2分
设![]() :
:![]() 解得
解得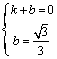 …3分
…3分
∴![]() 的表达式为
的表达式为![]() ……4分
……4分
⑶在![]() 上标出
上标出![]() 点,写出对应的
点,写出对应的![]() 点坐标:
点坐标: ,
,![]() ,
,
![]()
![]()
正确标出并写出一个给 2分
正确标出并写出二个给 4分
正确标出并写出三个给 5分
正确标出并写出四个给 6分