台州初级中学2005学年第一学期初三第四次统练试卷
数 学
一、选择题（每小题4分，共12小题，共48分）
1、在1.414、
、1.3、
、
、sin45°这六个数中，无理数有（ ）
A、4个 B、3个 C、2个 D、1个
2、函数
的自变量
的取值范围是（ ）
A、
B、>3 C、
D、<3
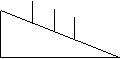3、如图，在坡度为1:2的山坡上种树，如果相邻两树之间的水平距离是4米，那么斜坡上相邻两树的坡面距离是（ ）
A、
米 B、
米 C、4米 D、
米
4、已知一次函数
与二次函数
，它们在同一坐标系内的图象大致是（ ）
 |
5、关于的一元二次方程
的一个根是0，则
的值为（ ）
A、―2 B、2 C、2或―2 D、0
6、随机抽取某城市30天的空气质量状况统计如下
| 污染指数( | 40 | 70 | 90 | 110 | 120 | 140 |
| 天数( | 3 | 5 | 10 | 7 | 4 | 1 |
)其中，
≤50时，空气质量最优；50＜≤100时，空气质量为良；100＜≤150时，空气质量为轻微污染，估计该城市一年（以365天计）中空气质量达到良好以上的天数为（ ）
A、
B、
C、
D、
7、应中共中央总书记胡锦涛同志的邀请，中国国民党主席连战先生、亲民党主席宋楚瑜先生分别从台湾来大陆参观访问，先后来到西安，都参观了新建成的“大唐芙蓉园”，该园占地面积约为800000m2，若按比例尺1:2000缩小后，其面积大约相当于（ ）
A、一个篮球场的面积 B、一张乒乓球台台面的面积
C、《浙江日报》的一个版面的面积 D、《数学》课本封面的面积
8、下列一元二次方程中，两实数根之和为2的是（ ）
A、
B、
C、
D、
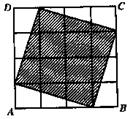9、如图，在一个由4×4个小正方形组成
的正方形网格中，阴影部分面积与正
方形ABCD面积的比是（ ）
A、3:4 B、5:8
C、9:16 D、1:2
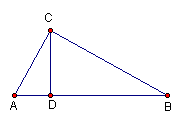10、如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，AC<BC，则下列结论中错误的是（ ）
A、CD2=AD·DB
B、AC·DB=BC·AD
C、AD·BC=AC·CD
D、BC2=BD·AB
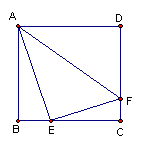
11、如图，在正方形ABCD中，点E、F分
别在边BC、CD上，如果AE=4，EF=3，
AF=5，那么正方形ABCD的面积等于（ ）
A、
B、
C、
D、
12、已知圆O的半径为5，P为圆O内一点，且OP=3，则过点P的所有弦中，弦长是整数的共有（ ）
A、4条 B、3条 C、2条 D、1条
二、填空题（每小题5分，共6小题，共30分）
13、方程
的实数解为
。
14、若
的两个根的差的平方是6，则=
。
15、函数
的图像与轴的交点的个数是
。
16、某地区开展“科技下乡”活动三年来，接受科技培训的人员累计达95万人次，其中第一年培训了20万人次，设每年接受科技培训的人次的平均增长率都为，根据题意列出的方程是
。
17、如图，在△ABC中，∠A=30°，
tanB=
，则AB= 。
18、一组按规律排列的数：
，请你推断第11个数是
。
三、解答题（共72分）
19、（6分）计算
20、（6分）已知
的值
21、（10分）某种洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续的过程，其中进水、清洗、排水时洗衣机中的水量
（升）与时间（分钟）之间的关系如折线图所示，根据图象解答下列问题：
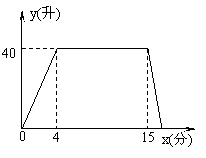（1）洗衣机的进水时间是多少分钟？
清洗时洗衣机中的水量是多少升？
（2）已知洗衣机的排水速度为每分钟19升：
①求排水时与之间的关系式；
②如果排水时间为2分钟，求排水结束
时洗衣机中剩下的水量。
22、（8分）如图，一人工湖的对岸有一条笔直的小
路，湖上原有一座小桥与小路垂直相通，现小
桥有一部分已断裂，另一部分完好，站在完好
的桥头A测得路边的小树D在它的北偏西30°，
前进32米到断口B处，又测得小树D在它的北
偏西45°，请计算小桥断裂部分的长（结果用
根号表示）。
23、（10分）在平面直角坐标系中，A（―1,0），B（3,0）。
（1）若抛物线过A、B两点，且与轴交于点
(0,―3)，求此抛物线的顶点坐标；
（2）如图，小敏发现所有过A、B两点的抛物线
如果与轴负半轴交于点C,M为抛物线的
顶点，那么△ACM与△ACB的面积比不变，
请你求出这个比值。
24、（10分）如图，已知圆内接四边形ABCD的两边AB、DC的延长线相交于点E，
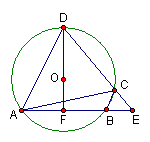DF过圆心O交AB于F，AF=FB，连接AC。
（1）求证：△ACD∽△EAD；
（2）若圆O的半径为5，AF=2BE=4，求证：AC=AD。
25、（10分）为了解决农民工子女入学难的问题，我市建立了一套进城农民工子
女就学的保障机制，其中一项就是免交“借读费”，据统计，2004年秋季有
5000名农民工子女进入主城区中小学学习，预测2005年秋季进入主城区中
小学学习的农民工子女将比2004年有所增加，其中小学增加20%，中学增加
30%，这样，2005年秋季将新增1160名农民工子女在主城区中小学学习。
（1）如果按小学每生每年收“借读费”500元，中学每生每年收“借读费”1000元计算，2005年新增的1160名中小学生共免收多少“借读费”？
（2）如果小学每40名学生配备2名教师，中学每40名学生配备3名教师，若按2005年秋季入学后，农民工子女在主城区中小学就读的学生人数计算，一共需要配备多少名中小学教师？
26、（12分）如图，抛物线经过点O(0,0)、A(4,0)、B(5,5)，点C是轴负半轴上一点，直线
经过B、C两点，且tan∠OCB=
。
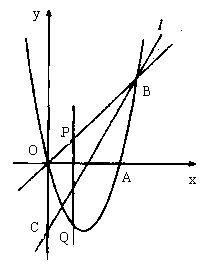（1）求抛物线的解析式
（2）求直线的解析式
（3）过O、B两点作直线，如果P是线段
OB上的一个动点，过点P作直线PQ
平行于轴，交抛物线于点Q，问：
是否存在点P，使得以P、Q、B为顶
点的三角形与△OBC相似？如果存在，
请求出点P的坐标，如果不存在，请
说明理由。
初三数学第四次统练试卷参考答案
一、选择（4×12=48分）
1-5、BBBCA 6-10、BCBBB 11-12、CA
二、填空（5×6=30分）
13、
14、
15、1或2
16、20+20（1+）+20（1+）2=95 17、5
18、
三、解答题（共72分）
19、（6分）
20、（6分）20
21、（10分）（1）4分钟 40升 （2）
2
22、（8分）
米
23、（10分）（1）顶点坐标（1，－4）
（2）设
由已知得
＞0
S△ABC=6
作MD⊥轴于D
S△ACM=S△ACO+ SOCMD－S△AMD=
∴S△ACM：S△ABC=1：6
24、（10分）（1）略
（2）连结OA，在Rt△AFO中，OF=3，DF=8
在Rt△DEF中，EF=6 ∴DE=10 ∵AE=10
∴DE=AE ∵△ACD∽△EAD ∴AC=AD
25、（10分）（1）设2004年秋季在主城区小学学习的农民工子女人，在主城区中学学习的农民工子女有人，则
∴
∴20%=680 30%=480
∴500×680+1000×480=820000（元）=82（万元）
（2）360名
26、（12分）（1）
（2）过点B作BD⊥轴于D，先求得C（0，－4）
∴
（3）当
时，△PBQ∽△OBC，抛物线与直线的交点就是
满足题意的点Q
∴
∴
（舍去）
∴
，
当
时，△PQB∽△OBC，又PB=
，OC=4 OB=5
代入解得
（舍去）
∴
，