2006年全国初中数学竞赛山东赛区预赛暨
2005年山东省初中数学竞赛试题
（2005年12月4日上午8∶30—11∶00）
一、选择题（本题共8小题，每小题6分，满分48分）：下面各题给出的选项中，只有一项是正确的，清江正确选项的代号填在题后的括号内.
1．化简
得 （ ）
A．
； B. 
;
C. 
; D. 
.
2．满足不等式组
的所有整数的个数为 （ ）
A.1 B.2 C.21 D.22
3．两个相似三角形，他们的周长分别是36和12.周长较大的三角形的最大边为15，周长较小的三角形的最小边为3，则周长较大的三角形的面积是（ ）
A.52 B.54 C.56 D.58
4．由一元二次方程x+px+q=0的两个根为p、q，则p、q等于 （ ）
A.0 B.1 C.0或-2 D.0或1
5．如图，△ABC中，∠B=400，AC的垂直平分线交AC于D，交BC于E,且∠EAB∶∠CAE=3∶1，则∠C等于（ ）
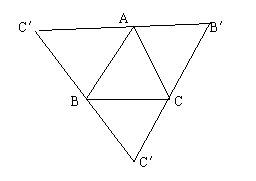A.270
B.250
C.22.50 D.200
 |
6．全班有70%的学生参加生物小组，75%的学生参加化学小组，85%的学生参加物理小组，90%的学生参加数学小组，则四个小组去参加的学生至少占全班的百分比是 （ ）
A.10% B.15% C.20% D.25%
7．有纯农药一桶，倒出20升后用水补满；然后又倒出10升，在用水补满，这是桶中纯
农药与水的容积之比为3∶5，则桶的容积为（ ）
A.30升 B.40升 C.50升 D.60升
8．三角形的三条外角平分线所在直线相交构成的三角形 （ ）
A.一定是锐角三角形; B.一定是钝角三角形;
C.一定是直角三角形; D.与原三角形相似
二、填空题（本提供4小题，每小题8分，满分32分）：将答案直接天再对应题目中的横线上
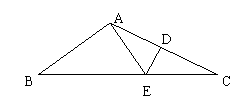
9．如图，在△ABC中，AB=AC, AD⊥BC, CG∥AB,
BG分别交AD,AC于E,F.若
，那么
等于
.
10.方程x-3+3x=1的解是 .
11．AD、BE、CF是△ABC的三条中线，若BC=a,CA=b,AB=c,
则AD2+BE2+CF2= .
12．有两个二位数，它们的差是58，它们的平方数的末两位数相同，则这个二位数是 .
三、解答题（本题共3小题，每小题20分，满分60分）
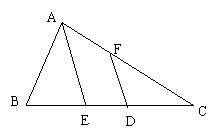13．△ABC中，AB=1,AC=2,D是BC中点,AE平分∠BAC交BC于E,且DF∥AE.求CF的长.
14．某建筑公司承包了两项工程，分别由两个工程队施工，根据工程进度情况，建筑公司可随时调整两队的人数，如果从甲队调70人到乙队，则乙队人数为甲队人数的2倍，如果从乙队调若干人去甲队，则甲队人数为乙队人数的3倍，问甲队至少有多少人？
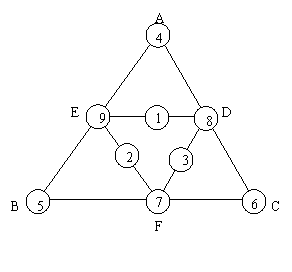
15．把数字1，2，3，…，9分别填入右图的9个圈内，要求三角形ABC和三角形DEF的每条边上三个圈内数字之和等于18.
Ⅰ给出符合要求的填法;
Ⅱ共有多少种不同填法？证明你的结论.
参考答案
一、选择题
DCBCA CBA
二、填空题
9．
10.-2或-1 11.
12.79和21
三、解答题
13．解：分别过E作EH⊥AB于H，EG⊥AC于G,因AE平分∠BAC,所以有EH=EG
从而有
又由DF∥AE,得
所以CF=
CA=
=
14.解：设甲队有x人，则乙队有[2(x-70)-70]人，即乙队有(2x-210)人
设从乙队调y人去甲队，甲队人数为乙队人数的3倍，则
3(2x-210-y)=x+y,
即
x=126+
y
由y>0知y至少为5，即x126+4=130.所以甲队至少有130人.
15.解：Ⅰ右图给出了一个符合要求的填法
Ⅱ共有6种不同填法
把填入A,B,C三处圈内的三个数字之和
记为x；D,E,F三处圈内的三个数字之和记为y；其余三圈
所填的数字之和为z.显然有x+y+z=1+2+…+9=45 ①
图中六条边，每条边上三个圈中之数的和为18，所以有
z+3y+2x=6×18=108 ②
②-①,得
X+2y=108-45=63 ③
把AB,BC,CA每一边上三圈中之数的和相加，则
可得 2x+y=3×18=54 ④
联立③，④，解得 x=15，y=24，继而之z=6.
在1，2，3，…，9种三个数之和为24的仅为7，8，9，
所以在D,E,F三处圈内，只能填7，8，9三个数，共有6种不同填法.
显然，当这三个圈中指数一旦确定，
根据题目要求，其余六个圈内指数也随之确定，
从而的结论，共有6种不同的填法.