
![]()
|
| |
一、选择题:(每题3Х8=24分)
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
|
1、方程![]() 2=5x的解是(
)
2=5x的解是(
)
A、x=0 B、x=5 C、x=0或x=5 D、x=1
2、下列命题中是真命题的是( )
A、有一个锐角和一条直角边相等的两个直角三角形全等;
B、腰长相等,有一个角是80°的两个等腰三角形全等;
C、、两边中垂线的交点在第三边上的三角形是直角三角形;
D、三角形中一边上的中线等于这边的一半;
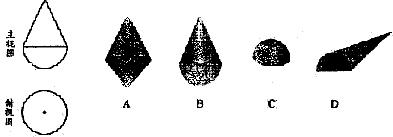
3、5.下列左边的主视图和俯视图对应右边的哪个物体 ( )

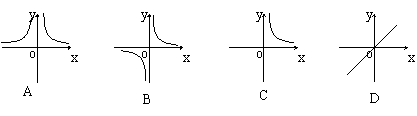
4、如果矩形的面积为6cm2,那么它的长![]() cm与宽
cm与宽![]() cm之间的函数关系用图象表示大致 ( )
cm之间的函数关系用图象表示大致 ( )
 | |||
 | |||
5、 如图,从A地沿北偏东30°方向走100m,到B地再从B地向西走200m到C地,这时小明离A地 ( ) 。
如图,从A地沿北偏东30°方向走100m,到B地再从B地向西走200m到C地,这时小明离A地 ( ) 。
A. 150m
B.100![]() m
m
C. 100m
D. 50![]() m
m
6. 有两组扑克牌各三张,牌面数字均为1,2,3,随意从每组牌中各抽一张,
数字和等于4的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、若反比例函数的图象经过(2,-2),(m,1),则m=( )
A. 1 B. -1 C. 4 D. -4
8、抛物线![]() 的顶点,当m取不同实数时,其顶点
的顶点,当m取不同实数时,其顶点
在下列( )上移动。
A、 ![]() B、y=2x
C、
B、y=2x
C、![]() D、
D、![]()
二、填空题(每题3Х7=21分)
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
9、命题“线段垂直平分线上的点,到这条线段的两个端点的距离相等”的
逆命题是______________________________________.
10、某钢铁厂今年1月份钢产量为4万吨,三月份钢产量为4.84万吨,每
月的增长率相同,问2、3月份平均每月的增长率是
11、在Rt△ABC中, ![]() ,则锐角
,则锐角![]() 的度数为_________.
的度数为_________.
12、将二次函数![]() 的图象向左平移3个单位,再向下平移4个单位,可以得到___________________的图象;
的图象向左平移3个单位,再向下平移4个单位,可以得到___________________的图象;
13、已知方程![]() 的一个根是-5,求它的另一个根是 ;
的一个根是-5,求它的另一个根是 ;
 14、如图,以正方形ABCD的对角线AC为一边,
14、如图,以正方形ABCD的对角线AC为一边,
延长AB到E,使AE = AC,以AE为一边作
菱形AEFC,若菱形的面积为![]() ,
,
则正方形边长
15、某同学利用用影子长度测量操场上旗杆的高度。在同一时刻,他测得自己的影子长为0. 8m,旗杆的影子长为7m,已知他的身高为1.6m,则旗杆的高度为________________.
三、解答题(16----19题每题6分,20题和21题每题7分,22题8分,
23题9分)
16、解方程:![]()
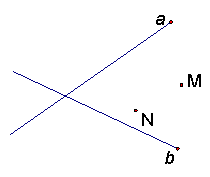
17、a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场。现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等。请用尺规画出O点位置,不写作法,保留痕迹。
18、在湖的两岸A、B间建一座观赏桥,由于条件限制,无法直接度量A、B两点间的距离。请你用学过的数学知识按以下要求设计一测量方案。
 (1)画出测量图案;
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算AB的距离(写出求解或推理过程,结果用字母表示)。
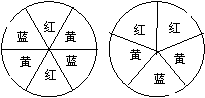
19、如图,用树状图或表格求右面两个转盘配成紫色的概率.
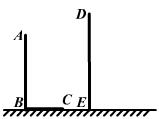
20、如图,AB和DE是直立在地面上的两根立柱。已知AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时立柱DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
 |
21、某商场将进货价为30元的的书包以40元售出,平均每月能售出600个。
调查表明:这种书包的售价每上涨1元,其销售量就减少10个。
(1) 为了实现平均每月10000的利润,这种书包的售价定为多少元?
(2) 10000元的利润是否为最大利润,请说明理由?如果不是,请求出最大利润,并指出此时书包的售价应定为多少元?
(3) 请分析回答售价在什么范围内商家就可获得利润?
23、如图,OABC是一张在平面直角坐标系中的矩形纸片,O为原点,点A在x
轴上,点C在y轴上, OA=10,OC=6,
(1) 如图,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作B/ 点,求B/点的坐标;
(2) 求折痕CM所在直线的解析式?
(3)  作B/ G//AB交CM于点G,若抛物线y=
作B/ G//AB交CM于点G,若抛物线y=![]() x2+m过点G,求抛物线的解析式?
x2+m过点G,求抛物线的解析式?
(4) 、CM所在的直线与抛物线的交点除点G之外,
还有几个交点坐标?并求出交点坐标?
 答案
答案